| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 18:12 ned, 18. 3. 2012 Naslov: Rješenja prošlogodišnjeg blica Postano: 18:12 ned, 18. 3. 2012 Naslov: Rješenja prošlogodišnjeg blica |
    |
|
|
Na zamolbu kolegice, riješio sam zadatke jedne grupe iz prošlogodišnjeg blica (možete naći u prilogu). Preporučam da prvo probate sami riješiti [url=http://web.math.pmf.unizg.hr/nastava/alg/2010-11/blic1.pdf]zadatke[/url], pa onda krenete čitati rješenja.
Molim vas da javite ovdje (ili na moj mail) ako primijetite bilo kakvu grešku.
Napomena za 2. zadatak: ne sjećam kako se on bodovao i što sam prošle godine napisao kao rješenje, ali poprilično siguran sam da je bilo bitno za sjetiti se kako se računa red permutacije i možda još komentirati nešto nakon toga.
Na zamolbu kolegice, riješio sam zadatke jedne grupe iz prošlogodišnjeg blica (možete naći u prilogu). Preporučam da prvo probate sami riješiti zadatke, pa onda krenete čitati rješenja.
Molim vas da javite ovdje (ili na moj mail) ako primijetite bilo kakvu grešku.
Napomena za 2. zadatak: ne sjećam kako se on bodovao i što sam prošle godine napisao kao rješenje, ali poprilično siguran sam da je bilo bitno za sjetiti se kako se računa red permutacije i možda još komentirati nešto nakon toga.
| Description: |
|

Download |
| Filename: |
AS_blic1_1011.pdf |
| Filesize: |
80.98 KB |
| Downloaded: |
2470 Time(s) |
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
|
| [Vrh] |
|
Buba 2
Forumaš(ica)

Pridružen/a: 13. 05. 2010. (09:44:05)
Postovi: (36)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
marlen
Forumaš(ica)


Pridružen/a: 01. 11. 2007. (23:42:26)
Postovi: (57)16
Lokacija: MedVEšČak
|
|
| [Vrh] |
|
kslaven
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (18:07:06)
Postovi: (52)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 17:28 čet, 22. 3. 2012 Naslov: Postano: 17:28 čet, 22. 3. 2012 Naslov: |
    |
|
|
Odaberi [latex](x_0,y_0)\in\mathbb{R}^2[/latex]. Trebaš naći [latex]x,y\in \mathbb{R}[/latex] td. je [latex]x+cy=x_0[/latex] i [latex]x+dy=y_0[/latex]. Oduzimanjem tih jednadžbi dolazimo do toga da mora vrijediti [latex](c-d)y=x_0-y_0[/latex].
Ako je c=d, onda je [latex]\psi(x,y)=(x+cy,x+cy)[/latex]. Odabremo li [latex](x_0,y_0)[/latex] da bude npr. (1,0), onda istovremeno mora biti x+cy=1 i x+cy=0, što nije moguće.
U preostalom slučaju eksplicitno se odrede x i y za koje je [latex]\psi(x,y)=(x_0,y_0)[/latex].
Odaberi 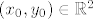 . Trebaš naći . Trebaš naći 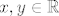 td. je td. je 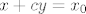 i i 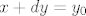 . Oduzimanjem tih jednadžbi dolazimo do toga da mora vrijediti . Oduzimanjem tih jednadžbi dolazimo do toga da mora vrijediti 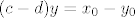 . .
Ako je c=d, onda je 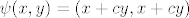 . Odabremo li . Odabremo li 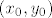 da bude npr. (1,0), onda istovremeno mora biti x+cy=1 i x+cy=0, što nije moguće. da bude npr. (1,0), onda istovremeno mora biti x+cy=1 i x+cy=0, što nije moguće.
U preostalom slučaju eksplicitno se odrede x i y za koje je 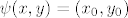 . .
_________________
The Dude Abides
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 11:25 pet, 23. 3. 2012 Naslov: Postano: 11:25 pet, 23. 3. 2012 Naslov: |
    |
|
|
[quote="Anonymous"]znači sad nam ostaje slučaj kad je c različito od d
i ako uzmemo (1,0) dobijemo y=1/(c-d) i x=-d/(c-d)
i sad pošto je to iz R2 vrijedi da je epimorfizam?[/quote]
Ne. Moraš provjeriti da [latex]\psi(x,y)=(x_0,y_0)[/latex] vrijedi za sve točke [latex](x_0,y_0)[/latex], ne samo za (1,0).
U prvom slučaju je bilo dovoljno naći samo jedan kontraprimjer, tj. jednu točku koju [latex]\psi[/latex] neće nikada pogoditi, a to je bila upravo (1,0) (iako se moglo na puno načina odabrati tu točku, npr. bilo koja točka (i,j), za i različito od j, bi bila dobar kontraprimjer).
Ako je c različito od d, onda je [latex]y=\frac{x_0-y_0}{c-d}[/latex] i [latex]x=y_0-d\cdot\frac{x_0-y_0}{c-d}[/latex]. Uvrsti to u funkciju i provjeri da vrijedi [latex]\psi(x,y)=(x_0,y_0)[/latex].
| Anonymous (napisa): | znači sad nam ostaje slučaj kad je c različito od d
i ako uzmemo (1,0) dobijemo y=1/(c-d) i x=-d/(c-d)
i sad pošto je to iz R2 vrijedi da je epimorfizam? |
Ne. Moraš provjeriti da 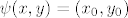 vrijedi za sve točke vrijedi za sve točke 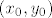 , ne samo za (1,0). , ne samo za (1,0).
U prvom slučaju je bilo dovoljno naći samo jedan kontraprimjer, tj. jednu točku koju 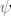 neće nikada pogoditi, a to je bila upravo (1,0) (iako se moglo na puno načina odabrati tu točku, npr. bilo koja točka (i,j), za i različito od j, bi bila dobar kontraprimjer). neće nikada pogoditi, a to je bila upravo (1,0) (iako se moglo na puno načina odabrati tu točku, npr. bilo koja točka (i,j), za i različito od j, bi bila dobar kontraprimjer).
Ako je c različito od d, onda je 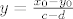 i i 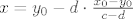 . Uvrsti to u funkciju i provjeri da vrijedi . Uvrsti to u funkciju i provjeri da vrijedi 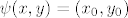 . .
_________________
The Dude Abides
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
blitzkrieg
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kslaven
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (18:07:06)
Postovi: (52)16
Spol: 
|
|
| [Vrh] |
|
blitzkrieg
Gost
|
|
| [Vrh] |
|
|











