| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 20:49 sri, 18. 4. 2012 Naslov: Postano: 20:49 sri, 18. 4. 2012 Naslov: |
    |
|
|
Ako su [tex]\left(\begin{matrix} a_1&b_1\\ 0&a_1^{-1} \end{matrix}\right)[/tex] i [tex]\left(\begin{matrix} a_2&b_2\\ 0&a_2^{-1} \end{matrix}\right)[/tex] dva predstavnika iste klase, onda je [tex]\left(\begin{matrix} a_1&b_1\\ 0&a_1^{-1} \end{matrix}\right) N=\left(\begin{matrix} a_2&b_2\\ 0&a_2^{-1} \end{matrix}\right) N[/tex] pa je [tex]\left(\begin{matrix} a_1^{-1}&-b_1\\ 0&a_1 \end{matrix}\right)\cdot\left(\begin{matrix} a_2&b_2\\ 0&a_2^{-1} \end{matrix}\right)\in N[/tex], odnosno [tex]a_1^{-1}a_2=1[/tex] i još je [tex]a_1a_2^{-1}=1[/tex] pa je [tex]a_1=a_2[/tex], tj. [tex]f\left(\left(\begin{matrix} a_1&b_1\\ 0&a_1^{-1} \end{matrix}\right) N\right)=f\left(\left(\begin{matrix} a_2&b_2\\ 0&a_2^{-1} \end{matrix}\right) N\right).[/tex] Dakle, funkcija f je dobro definirana.
Jer je [tex]\left(\begin{matrix} a_1&x\\ 0&a_1^{-1} \end{matrix}\right)\cdot\left(\begin{matrix} a_2&y\\ 0&a_2^{-1} \end{matrix}\right)=\left(\begin{matrix} a_1a_2&z\\ 0&(a_2a_1)^{-1} \end{matrix}\right)=\left(\begin{matrix} a_1a_2&z\\ 0&(a_1a_2)^{-1} \end{matrix}\right)[/tex] onda se lako provjeri da je f homomorfizam.
Očito je epimorfizam jer za [tex]a\in\mathbb{R}^\times[/tex] je [tex]f(mN)=a[/tex], pri čemu je [tex]m[/tex] matrica koja na mjestu (1,1) ima broj [tex]a[/tex], a biti će izomorfizam akko mu je jezgra trivijalna, tj. akko je ker f = N. To ostavljam vama da provjerite. :)
Ako su [tex]\left(\begin{matrix} a_1&b_1\\ 0&a_1^{-1} \end{matrix}\right)[/tex] i [tex]\left(\begin{matrix} a_2&b_2\\ 0&a_2^{-1} \end{matrix}\right)[/tex] dva predstavnika iste klase, onda je [tex]\left(\begin{matrix} a_1&b_1\\ 0&a_1^{-1} \end{matrix}\right) N=\left(\begin{matrix} a_2&b_2\\ 0&a_2^{-1} \end{matrix}\right) N[/tex] pa je [tex]\left(\begin{matrix} a_1^{-1}&-b_1\\ 0&a_1 \end{matrix}\right)\cdot\left(\begin{matrix} a_2&b_2\\ 0&a_2^{-1} \end{matrix}\right)\in N[/tex], odnosno [tex]a_1^{-1}a_2=1[/tex] i još je [tex]a_1a_2^{-1}=1[/tex] pa je [tex]a_1=a_2[/tex], tj. [tex]f\left(\left(\begin{matrix} a_1&b_1\\ 0&a_1^{-1} \end{matrix}\right) N\right)=f\left(\left(\begin{matrix} a_2&b_2\\ 0&a_2^{-1} \end{matrix}\right) N\right).[/tex] Dakle, funkcija f je dobro definirana.
Jer je [tex]\left(\begin{matrix} a_1&x\\ 0&a_1^{-1} \end{matrix}\right)\cdot\left(\begin{matrix} a_2&y\\ 0&a_2^{-1} \end{matrix}\right)=\left(\begin{matrix} a_1a_2&z\\ 0&(a_2a_1)^{-1} \end{matrix}\right)=\left(\begin{matrix} a_1a_2&z\\ 0&(a_1a_2)^{-1} \end{matrix}\right)[/tex] onda se lako provjeri da je f homomorfizam.
Očito je epimorfizam jer za [tex]a\in\mathbb{R}^\times[/tex] je [tex]f(mN)=a[/tex], pri čemu je [tex]m[/tex] matrica koja na mjestu (1,1) ima broj [tex]a[/tex], a biti će izomorfizam akko mu je jezgra trivijalna, tj. akko je ker f = N. To ostavljam vama da provjerite. 
_________________
The Dude Abides
Zadnja promjena: goranm; 22:07 sri, 18. 4. 2012; ukupno mijenjano 5 put/a.
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 21:44 sri, 18. 4. 2012 Naslov: Postano: 21:44 sri, 18. 4. 2012 Naslov: |
    |
|
|
[quote="Bug"]mozda ovako nesto:
[latex](g_1 H)( g_2 H)=(g_2 H)( g_1 H)[/latex]
[latex]g_1^{-1}g_2^{-1}/ g_1 g_2 H=g_2 g_1H[/latex]
[latex]g_1^{-1}g_2^{-1}g_1 g_2 H=H[/latex]
i sad pokazati da vrijedi [latex]g_1^{-1}g_2^{-1}g_1 g_2 \in H[/latex]
tako jel??[/quote]
Ne. Što je H, a što su g1 i g2? Zašto započinješ s [latex](g_1 H)( g_2 H)=(g_2 H)( g_1 H)[/latex]? To ne vrijedi općenito, to vrijedi samo ako je G/H komutativna grupa,a u ovom trenutku ne znam ni što ti je G, niti što ti je H.
Što znači [latex]g_1^{-1}g_2^{-1}/ g_1 g_2 H=g_2 g_1H[/latex]? Ovdje kvocijent [latex]g_1^{-1}g_2^{-1}/ g_1 g_2 H[/latex] nije dobro definiran.
| Bug (napisa): | mozda ovako nesto:
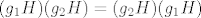
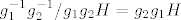
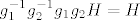
i sad pokazati da vrijedi 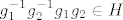
tako jel?? |
Ne. Što je H, a što su g1 i g2? Zašto započinješ s 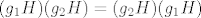 ? To ne vrijedi općenito, to vrijedi samo ako je G/H komutativna grupa,a u ovom trenutku ne znam ni što ti je G, niti što ti je H. ? To ne vrijedi općenito, to vrijedi samo ako je G/H komutativna grupa,a u ovom trenutku ne znam ni što ti je G, niti što ti je H.
Što znači 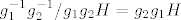 ? Ovdje kvocijent ? Ovdje kvocijent 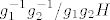 nije dobro definiran. nije dobro definiran.
_________________
The Dude Abides
Zadnja promjena: goranm; 21:50 sri, 18. 4. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
 Postano: 21:58 sri, 18. 4. 2012 Naslov: Postano: 21:58 sri, 18. 4. 2012 Naslov: |
    |
|
|
[quote="goranm"][quote="Bug"]mozda ovako nesto:
[latex](g_1 H)( g_2 H)=(g_2 H)( g_1 H)[/latex]
[latex]g_1^{-1}g_2^{-1}/ g_1 g_2 H=g_2 g_1H[/latex]
[latex]g_1^{-1}g_2^{-1}g_1 g_2 H=H[/latex]
i sad pokazati da vrijedi [latex]g_1^{-1}g_2^{-1}g_1 g_2 \in H[/latex]
tako jel??[/quote]
Ne. Što je H, a što su g1 i g2? Zašto započinješ s [latex](g_1 H)( g_2 H)=(g_2 H)( g_1 H)[/latex]? To ne vrijedi općenito, to vrijedi samo ako je G/H komutativna grupa,a u ovom trenutku ne znam ni što ti je G, niti što ti je H.
Što znači [latex]g_1^{-1}g_2^{-1}/ g_1 g_2 H=g_2 g_1H[/latex]? Ovdje kvocijent [latex]g_1^{-1}g_2^{-1}/ g_1 g_2 H[/latex] nije dobro definiran.[/quote]
Ma krivo sam stavio... umjesto H trebalo jhe pisati N, a [latex]g_1 i g_2 [/latex] su iz G
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
[quote="pravipurger"][quote="goranm"]
Što znači [latex]g_1^{-1}g_2^{-1}/ g_1 g_2 H=g_2 g_1H[/latex]? Ovdje kvocijent [latex]g_1^{-1}g_2^{-1}/ g_1 g_2 H[/latex] nije dobro definiran.[/quote]
Kolega je krenuo dokazivat komutativnost umjesto injektivnosti.
To, ako ja dobro shvaćam, nije kvocijent već prikaz kao da (g_1)^-1 i (g_2)^-1 dijeluju na g1g2[/quote]
da bas to :)
| goranm (napisa): | | Bug (napisa): | mozda ovako nesto:
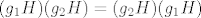
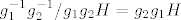
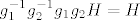
i sad pokazati da vrijedi 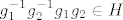
tako jel?? |
Ne. Što je H, a što su g1 i g2? Zašto započinješ s 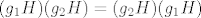 ? To ne vrijedi općenito, to vrijedi samo ako je G/H komutativna grupa,a u ovom trenutku ne znam ni što ti je G, niti što ti je H. ? To ne vrijedi općenito, to vrijedi samo ako je G/H komutativna grupa,a u ovom trenutku ne znam ni što ti je G, niti što ti je H.
Što znači 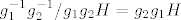 ? Ovdje kvocijent ? Ovdje kvocijent 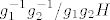 nije dobro definiran. nije dobro definiran. |
Ma krivo sam stavio... umjesto H trebalo jhe pisati N, a 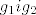 su iz G su iz G
Added after 2 minutes:
| pravipurger (napisa): | | goranm (napisa): |
Što znači 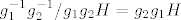 ? Ovdje kvocijent ? Ovdje kvocijent 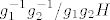 nije dobro definiran. nije dobro definiran. |
Kolega je krenuo dokazivat komutativnost umjesto injektivnosti.
To, ako ja dobro shvaćam, nije kvocijent već prikaz kao da (g_1)^-1 i (g_2)^-1 dijeluju na g1g2 |
da bas to 
_________________
Everybody Dies...
Nobody is perfect...
Non scholae, sed vitae discimus
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 10:17 čet, 19. 4. 2012 Naslov: Postano: 10:17 čet, 19. 4. 2012 Naslov: |
    |
|
|
[quote="Anonymous"]ja sam dobila da nije izomorfizam, jel to točno?[/quote]
Ja mislim da je suprotno...A evo zašto tako mislim:
ako uzmeš bilo koje dvije različite klase, sigurno će ih preslikati u različite elemente R-a pošto je već gore pokazano da bi dva elementa bila u istoj klasi mora bit x1=x2, onda ako su u različitim klasama onda x1!=x2, a onda ih preslikava u različite elemente. Pa po tome injektivnost vrijedi, a surjektivnost također jer koji god nenul broj uzmeš, recimo x, možeš ga preslikati nazad u matricu koja izgleda ovako
(x b)
(0 x)
pri cemu b može biti bilo što pošto je iz R. A ta matrica ponovo određuje točno jednu klasu, bez obzira na b.
Nisam siguran da je sve ovo što sam napisao točno, ali eto to je moje mišljenje...
| Anonymous (napisa): | | ja sam dobila da nije izomorfizam, jel to točno? |
Ja mislim da je suprotno...A evo zašto tako mislim:
ako uzmeš bilo koje dvije različite klase, sigurno će ih preslikati u različite elemente R-a pošto je već gore pokazano da bi dva elementa bila u istoj klasi mora bit x1=x2, onda ako su u različitim klasama onda x1!=x2, a onda ih preslikava u različite elemente. Pa po tome injektivnost vrijedi, a surjektivnost također jer koji god nenul broj uzmeš, recimo x, možeš ga preslikati nazad u matricu koja izgleda ovako
(x b)
(0 x)
pri cemu b može biti bilo što pošto je iz R. A ta matrica ponovo određuje točno jednu klasu, bez obzira na b.
Nisam siguran da je sve ovo što sam napisao točno, ali eto to je moje mišljenje...
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 16:07 čet, 19. 4. 2012 Naslov: Postano: 16:07 čet, 19. 4. 2012 Naslov: |
    |
|
|
[quote="Anonymous"]ja sam dobila da nije izomorfizam, jel to točno?[/quote]
Nije. Neka je [tex]\left(\begin{matrix}a&b\\0&a^{-1}\end{matrix}\right)N \in \ker f[/tex].
Onda je [tex]f\left(\left(\begin{matrix}a&b\\0&a^{-1}\end{matrix}\right)N\right)=1[/tex], pa je a=1 i još [tex]\left(\begin{matrix}a&b\\0&a^{-1}\end{matrix}\right)=\left(\begin{matrix}1&b\\0&1\end{matrix}\right)[/tex]. Jer je [tex]\left(\begin{matrix}1&b\\0&1\end{matrix}\right) \in N[/tex], onda je [tex]\left(\begin{matrix}1&b\\0&1\end{matrix}\right)N=N[/tex]. Dakle, [tex]\ker f \subseteq N[/tex].
Obratno, ako je [tex]\left(\begin{matrix}a&b\\0&a^{-1}\end{matrix}\right) \in N[/tex], onda je a=1 pa je [tex]f\left(\left(\begin{matrix}a&b\\0&a^{-1}\end{matrix}\right)N\right)=a=1[/tex], tj. [tex]\left(\begin{matrix}a&b\\0&a^{-1}\end{matrix}\right)N \in \ker f[/tex] pa je [tex]N\subseteq \ker f[/tex].
Dakle, ker f = N pa je homomorfizam f monomorfizam. Ranije je ustanovljeno da je epimorfizam pa je i izomorfizam
| Anonymous (napisa): | | ja sam dobila da nije izomorfizam, jel to točno? |
Nije. Neka je [tex]\left(\begin{matrix}a&b\\0&a^{-1}\end{matrix}\right)N \in \ker f[/tex].
Onda je [tex]f\left(\left(\begin{matrix}a&b\\0&a^{-1}\end{matrix}\right)N\right)=1[/tex], pa je a=1 i još [tex]\left(\begin{matrix}a&b\\0&a^{-1}\end{matrix}\right)=\left(\begin{matrix}1&b\\0&1\end{matrix}\right)[/tex]. Jer je [tex]\left(\begin{matrix}1&b\\0&1\end{matrix}\right) \in N[/tex], onda je [tex]\left(\begin{matrix}1&b\\0&1\end{matrix}\right)N=N[/tex]. Dakle, [tex]\ker f \subseteq N[/tex].
Obratno, ako je [tex]\left(\begin{matrix}a&b\\0&a^{-1}\end{matrix}\right) \in N[/tex], onda je a=1 pa je [tex]f\left(\left(\begin{matrix}a&b\\0&a^{-1}\end{matrix}\right)N\right)=a=1[/tex], tj. [tex]\left(\begin{matrix}a&b\\0&a^{-1}\end{matrix}\right)N \in \ker f[/tex] pa je [tex]N\subseteq \ker f[/tex].
Dakle, ker f = N pa je homomorfizam f monomorfizam. Ranije je ustanovljeno da je epimorfizam pa je i izomorfizam
_________________
The Dude Abides
|
|
| [Vrh] |
|
|












