| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
KG
Forumaš(ica)
Pridružen/a: 26. 01. 2011. (15:50:24)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 13:02 pet, 1. 6. 2012 Naslov: Postano: 13:02 pet, 1. 6. 2012 Naslov: |
    |
|
|
Jedan način je da integral po rubu parametriziraš u polarnim koordinatama, a po krugu (kao u dokazu Greenovog teorema za jedinični kvadrat) koristeći Fubinijev tm i Newton-Leibnizovu formulu integriraš u pravokutnim koordinatama i riješiš se parcijalnih derivacija. Zatim trigonometrijskim supstitucijama svedeš na ovaj po rubu. Morat ćeš jako paziti na predznake i da supstitucije budu injektivne (npr. sinus je injektivan na [latex][-\frac{\pi}{2}, \frac{\pi}{2}][/latex], ali ne na [latex][0, \pi][/latex]).
Sve u svemu, ima puno posla. :D Ako negdje zapneš, reci.
Jedan način je da integral po rubu parametriziraš u polarnim koordinatama, a po krugu (kao u dokazu Greenovog teorema za jedinični kvadrat) koristeći Fubinijev tm i Newton-Leibnizovu formulu integriraš u pravokutnim koordinatama i riješiš se parcijalnih derivacija. Zatim trigonometrijskim supstitucijama svedeš na ovaj po rubu. Morat ćeš jako paziti na predznake i da supstitucije budu injektivne (npr. sinus je injektivan na 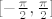 , ali ne na , ali ne na 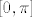 ). ).
Sve u svemu, ima puno posla.  Ako negdje zapneš, reci. Ako negdje zapneš, reci.
|
|
| [Vrh] |
|
KG
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (15:50:24)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
|
| [Vrh] |
|
KG
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (15:50:24)
Postovi: (30)16
Spol: 
|
 Postano: 19:22 sub, 2. 6. 2012 Naslov: Postano: 19:22 sub, 2. 6. 2012 Naslov: |
    |
|
|
E ovak... Imaš u skripti dokaz Greenovog teorema za jedinični kvadrat pa prvo to prođi da vidiš malo na jednostavnom primjeru kak se rade supstitucije, mijenjaju granice i slično. Radi se u 3 koraka: 1. raspišeš integral po području, 2. raspišeš integral po rubu područja i 3. radiš supstitucije dok ne dobiješ da su te dvije stvari iste :D Ugl, kad se raspiše dvostruki intgral po krugu dobiješ ukupno 4 jednostruka integrala svi u granicama od -r do r. Ovaj drugi dio "ovisi" o putu koji uzmeš da opišeš kružnicu...ja sam uzeo od -pi do pi (r*cost, r*sint) i tak dobiješ 2 jednostruka integrala od -pi do pi. Na kraju radiš supstitucije u ovom prvom izrazu oblika x=r*cost , y=r*sint i moraš dobit ovaj drugi izraz. Nisam baš vičan u latexu pa ti ne mogu izraze napisat preciznije.....valjda ti ovo pomaže, a imaš i tu na forumu raspisan Green za trapez: http://degiorgi.math.hr/forum/viewtopic.php?t=16799[/tt][/table]
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
Ups...krivi link..Tu je raspisano: http://degiorgi.math.hr/forum/viewtopic.php?t=13348
E ovak... Imaš u skripti dokaz Greenovog teorema za jedinični kvadrat pa prvo to prođi da vidiš malo na jednostavnom primjeru kak se rade supstitucije, mijenjaju granice i slično. Radi se u 3 koraka: 1. raspišeš integral po području, 2. raspišeš integral po rubu područja i 3. radiš supstitucije dok ne dobiješ da su te dvije stvari iste  Ugl, kad se raspiše dvostruki intgral po krugu dobiješ ukupno 4 jednostruka integrala svi u granicama od -r do r. Ovaj drugi dio "ovisi" o putu koji uzmeš da opišeš kružnicu...ja sam uzeo od -pi do pi (r*cost, r*sint) i tak dobiješ 2 jednostruka integrala od -pi do pi. Na kraju radiš supstitucije u ovom prvom izrazu oblika x=r*cost , y=r*sint i moraš dobit ovaj drugi izraz. Nisam baš vičan u latexu pa ti ne mogu izraze napisat preciznije.....valjda ti ovo pomaže, a imaš i tu na forumu raspisan Green za trapez: http://degiorgi.math.hr/forum/viewtopic.php?t=16799[/tt][/table] Ugl, kad se raspiše dvostruki intgral po krugu dobiješ ukupno 4 jednostruka integrala svi u granicama od -r do r. Ovaj drugi dio "ovisi" o putu koji uzmeš da opišeš kružnicu...ja sam uzeo od -pi do pi (r*cost, r*sint) i tak dobiješ 2 jednostruka integrala od -pi do pi. Na kraju radiš supstitucije u ovom prvom izrazu oblika x=r*cost , y=r*sint i moraš dobit ovaj drugi izraz. Nisam baš vičan u latexu pa ti ne mogu izraze napisat preciznije.....valjda ti ovo pomaže, a imaš i tu na forumu raspisan Green za trapez: http://degiorgi.math.hr/forum/viewtopic.php?t=16799[/tt][/table]
Added after 2 minutes:
Ups...krivi link..Tu je raspisano: http://degiorgi.math.hr/forum/viewtopic.php?t=13348
|
|
| [Vrh] |
|
|









