povezanost putevima (zadatak)

[Loo]

http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/DRFVVkol_1.pdf

može li netko pokazati 8.?
zapela sam pred kraj dokaza.
krenula sam ovako:
budući da je presjek neprazan, znamo da postoji neki [tex]c[/tex] u tom presjeku i taj [tex]c[/tex] je u svakom [tex]Ai[/tex]. za proizvoljne [tex]x, y[/tex] iz unije znamo da postoje [tex]i,j\in I[/tex] t.d je [tex]x\in Ai, y\in Aj[/tex]. ako je [tex]i=j[/tex], onda sigurno postoji put između [tex]x[/tex] i [tex]y[/tex] jer je [tex]Ai[/tex] povezan putevima. sad gledam za [tex]i\neq j[/tex].
budući da je [tex]c\in Ai, c\in Aj[/tex], a oni su povezani putevima sigurno postoji put, odnosno neprekidno preslikavanje [tex]\alpha:[a, b]\rightarrow R^n[/tex] t.d. [tex]\alpha(a)=x, \alpha(b)=c[/tex]. i isto tako postoji i drugo neprekidno preslikavanje [tex]\beta[/tex] u [tex]Aj[/tex] za [tex]c[/tex] i [tex]y[/tex]. mene muči kako ta dva puta povezati u jedan? ili je ovo dovoljna argumentacija?

[goranm]

Nije dovoljno jer jos trebas argumentirati zasto bi spoj puteva [tex]\alpha[/tex] i [tex]\beta[/tex] bio put, tj. zasto je taj spoj uopce dobro definirana funkcija i zasto je neprekidna. Ako je [tex]\beta\colon[b,d]\to A_j[/tex] td. [tex]\beta(b)=c[/tex] i [tex]\beta(d)=y[/tex], onda definiraj [tex]\gamma\colon [a,d]\to A_i\cup A_j[/tex] td. je

[tex]\gamma(t)=\left\{\begin{array}{rl}
\alpha(t), & t\in [a,b],\\
\beta(t), & t\in [b,d].
\end{array}\right.[/tex]

To je dobro definirana funkcija jer je [tex]\alpha(b)=\beta(b)[/tex], a neprekidna je jer su [tex]\alpha[/tex] i [tex]\beta[/tex] neprekidne i podudaraju se na presjeku njihovih domena. Prema tome, to je put u [tex]\cup_{i\in I}A_i[/tex] od x do y.

_________________
The Dude Abides

[Loo]

i mislila sam da treba, ali nisam bila sigurna smijem li staviti da [tex]\beta[/tex] preslikava baš segment koji počinje sa [tex]b[/tex], budući da [tex]\alpha [/tex] i [tex]\beta[/tex] mogu biti skroz drugačija preslikavanja.

hvala!

[goranm]

Btw. ako su skupovi [tex]A_i[/tex] povezani putevima u [tex]\mathbb{R}^n[/tex], onda [tex]\alpha \colon [a,b] \to \mathbb{R}^n[/tex] td. je [tex]\alpha(a)=x[/tex], [tex]\alpha(b)=c[/tex] nije nuzno put u [tex]A_i[/tex]. S obzirom da si za kodomenu stavila [tex]\mathbb{R}^n[/tex], to znaci da (bes)konacno mnogo tocaka tog puta moze ispasti izvan citave unije [tex]\cup A_i[/tex]. Prema tome, za tako definiranu funkciju [tex]\alpha[/tex], prethodna argumentacija da je unija [tex]\cup A_i[/tex] povezana putevima ne bi bila dobra.

To se lagano ispravi tako da za kodomenu funkcije [tex]\alpha[/tex] uzmes [tex]A_i[/tex].

_________________
The Dude Abides

[Loo]

aha, istina, zaboravila sam spomenuti [tex]\alpha([a,b])\subset Ai[/tex]

[goranm]

[Loo]

aha, a sad shvaćam! iako mi je bilo intuitivno jasno što je put, nisam znala da imamo toliku slobodu pri odabiru intervala. puno hvala, ovo bi moglo biti korisno

[nuclear]

Je li točno da ukoliko je funkcija neprekidna da preslikava svaka dva disjunktna skupa B i C iz u opet disjunktna skupa iz A? Nisam sigurna da mi je najjasnija ta povezanost putevima.

[Loo]

hoćeš reći da su praslike po [tex]f[/tex] dvaju disjunktnih skupova iz [tex]Rk[/tex], disjunktne u [tex]A[/tex]? pa to je osnovno funkcijsko pravilo, kada bi neki [tex]x[/tex] bio u presjeku te dvije praslike, to bi značilo da je [tex]f(x)\in B[/tex] i [tex]f(x)\in C[/tex], a budući da su [tex]B[/tex] i [tex]C[/tex] disjunktni ispalo bi da [tex]f[/tex] šalje [tex]x[/tex] u dvije različite vrijednosti.

[nuclear]

Zašto bi vrijedila "ako i samo ako" za tvrdnju: Otvoren skup u 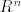je povezan akko je povezan putevima; ? Ako znamo da ako je skup povezan putevima onda je intuitivno i povezan. Vrijedi li ista relacija i za zatvoren skup?

[kikzmyster]

Evo, pogledaj ovo: http://degiorgi.math.hr/forum/viewtopic.php?t=17275

[goranm]