| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 20:44 ned, 11. 11. 2012 Naslov: Postano: 20:44 ned, 11. 11. 2012 Naslov: |
    |
|
|
[quote="Anonymous"][quote="Anonymous"]A jel bi netko mogao 3.2 ?[/quote]
Pridružio bih se gornjem pitanju.
3.2 Dokažite da je svojstveni polinom [latex]k_A (x)[/latex] operatora [latex]A \in L(V)[/latex] normirani polinom stupnja [latex]n = dim V[/latex].
Zar nije minimalan taj koji je normiran, a karakteristični ne mora nužno biti?
I kako pokazati da je karakteristični polinom baš stupnja n?
Hvala! :D[/quote]
Lakši način: Sve slične matrice imaju isti svojstveni polinom. Svaku matricu možemo dovesti u Jordanovu formu. Matrica u Jordanovoj formi je gornjetrokutasta, pa je njena determinanta umnožak elemenata na dijagonali. To je praktički to, samo treba malo formalizirati. :D
Teži način: Indukcijom, koristeći Laplaceov razvoj matrice.
Ako treba dodatno objasniti koji od ova dva načina, samo pitajte.
EDIT: Zapravo, ne bih rekao da je teži način teži, već samo malo nezgrapniji. :D
| Anonymous (napisa): | | Anonymous (napisa): | | A jel bi netko mogao 3.2 ? |
Pridružio bih se gornjem pitanju.
3.2 Dokažite da je svojstveni polinom 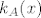 operatora operatora 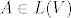 normirani polinom stupnja normirani polinom stupnja 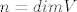 . .
Zar nije minimalan taj koji je normiran, a karakteristični ne mora nužno biti?
I kako pokazati da je karakteristični polinom baš stupnja n?
Hvala!  |
Lakši način: Sve slične matrice imaju isti svojstveni polinom. Svaku matricu možemo dovesti u Jordanovu formu. Matrica u Jordanovoj formi je gornjetrokutasta, pa je njena determinanta umnožak elemenata na dijagonali. To je praktički to, samo treba malo formalizirati. 
Teži način: Indukcijom, koristeći Laplaceov razvoj matrice.
Ako treba dodatno objasniti koji od ova dva načina, samo pitajte.
EDIT: Zapravo, ne bih rekao da je teži način teži, već samo malo nezgrapniji. 
|
|
| [Vrh] |
|
|





