| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Juraj Siftar
Gost
|
 Postano: 6:03 čet, 26. 1. 2012 Naslov: Zadaci s popravnog kolokvija 25. siječnja 2012. Postano: 6:03 čet, 26. 1. 2012 Naslov: Zadaci s popravnog kolokvija 25. siječnja 2012. |
    |
|
|
Popravni kolokvij:
1. Definirajte sljedeće pojmove: unitarni prostor
(što obuhvaća definiciju skalarnog produkta),
ortogonalna projekcija vektora na potprostor L unitarnog
prostora V, matrica linearnog operatora u odabranom paru
baza, matrica prijelaza između dvije baze vektorskog
prostora, sličnost dviju kvadratnih matrica (15 bodova).
2. Odredite neku bazu (a,b,c) prostora V3(O) tako da
a i b zatvaraju kut π/4, a c sa svakim od a i b kut π/3.
Izračunajte ortogonalnu projekciju c na potprostor [a,b]
te udaljenost c od tog potprostora. Napišite matricu tog
operatora projekcije, u bazi (i,j,k). (20 bodova)
3. Neka su K, L < M3(R) potprostori koje čine sve takve matrice
reda 3 da im je zbroj koeficijenata svakog retka jednak 0 (za K),
odnosno zbroj koeficijenata svakog stupca jednak 0 (za L).
Pokažite da su K i L izomorfni potprostori te zadajte neki
izomorfizam među njima.(10 bodova)
4. Ako je D operator deriviranja na prostoru P3 polinoma
stupnja najviše 3, pokažite da za linearni operator I+D postoji
inverzni operator (I je jedinični) te izračunajte (I+D)(-1)(f),
za f(x) = 1+x+x2+x3. (20 bodova)
5. Linearni operator A na prostoru R4 zadan je u kanonskoj
bazi matricom [aij] tako da je aij=(-1)i+j. Odredite svojstvene
potprostore operatora A. Ako se A može dijagonalizirati u nekoj ortonormiranoj bazi,
nađite takvu bazu i dijagonalni oblik. (20 bodova)
6. Neka su λ1,λ2 dvije različite svojetvene vrijednosti
linearnog operatora A, a v1 i v2 neki njima pridruženi
svojstveni vektori. Dokažite da je skup {v1,v2} linearno
nezavisan.
(15 bodova).
Napomene:
Zadatak gotovo identičan 4. zadatku bio je u obaveznoj domaćoj
zadaći, zadatak vrlo sličan 2. zadatku također,
a nitko nije riješio 5. zadatak, standardni zadatak
dijagonalizacije jednostavne matrice
ranga 1 čiji su koeficijenti naizmjence 1 i -1.
Samo troje studenata dobilo je neke značajnije bodove u 1. zadatku
gdje se traže definicije nekih od najvažnijih pojmova i koncepata
iz kolegija.
Neki još uvijek ne vide ništa sumnjivo u računu kojim za
svojstveni vektor dobivaju nulvektor.
Popravni kolokvij:
1. Definirajte sljedeće pojmove: unitarni prostor
(što obuhvaća definiciju skalarnog produkta),
ortogonalna projekcija vektora na potprostor L unitarnog
prostora V, matrica linearnog operatora u odabranom paru
baza, matrica prijelaza između dvije baze vektorskog
prostora, sličnost dviju kvadratnih matrica (15 bodova).
2. Odredite neku bazu (a,b,c) prostora V3(O) tako da
a i b zatvaraju kut π/4, a c sa svakim od a i b kut π/3.
Izračunajte ortogonalnu projekciju c na potprostor [a,b]
te udaljenost c od tog potprostora. Napišite matricu tog
operatora projekcije, u bazi (i,j,k). (20 bodova)
3. Neka su K, L < M3(R) potprostori koje čine sve takve matrice
reda 3 da im je zbroj koeficijenata svakog retka jednak 0 (za K),
odnosno zbroj koeficijenata svakog stupca jednak 0 (za L).
Pokažite da su K i L izomorfni potprostori te zadajte neki
izomorfizam među njima.(10 bodova)
4. Ako je D operator deriviranja na prostoru P3 polinoma
stupnja najviše 3, pokažite da za linearni operator I+D postoji
inverzni operator (I je jedinični) te izračunajte (I+D)(-1)(f),
za f(x) = 1+x+x2+x3. (20 bodova)
5. Linearni operator A na prostoru R4 zadan je u kanonskoj
bazi matricom [aij] tako da je aij=(-1)i+j. Odredite svojstvene
potprostore operatora A. Ako se A može dijagonalizirati u nekoj ortonormiranoj bazi,
nađite takvu bazu i dijagonalni oblik. (20 bodova)
6. Neka su λ1,λ2 dvije različite svojetvene vrijednosti
linearnog operatora A, a v1 i v2 neki njima pridruženi
svojstveni vektori. Dokažite da je skup {v1,v2} linearno
nezavisan.
(15 bodova).
Napomene:
Zadatak gotovo identičan 4. zadatku bio je u obaveznoj domaćoj
zadaći, zadatak vrlo sličan 2. zadatku također,
a nitko nije riješio 5. zadatak, standardni zadatak
dijagonalizacije jednostavne matrice
ranga 1 čiji su koeficijenti naizmjence 1 i -1.
Samo troje studenata dobilo je neke značajnije bodove u 1. zadatku
gdje se traže definicije nekih od najvažnijih pojmova i koncepata
iz kolegija.
Neki još uvijek ne vide ništa sumnjivo u računu kojim za
svojstveni vektor dobivaju nulvektor.
|
|
| [Vrh] |
|
sstudentica
Forumaš(ica)
Pridružen/a: 30. 11. 2010. (13:18:02)
Postovi: (3A)16
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
|
| [Vrh] |
|
sstudentica
Forumaš(ica)
Pridružen/a: 30. 11. 2010. (13:18:02)
Postovi: (3A)16
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
|
| [Vrh] |
|
sstudentica
Forumaš(ica)
Pridružen/a: 30. 11. 2010. (13:18:02)
Postovi: (3A)16
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
 Postano: 1:29 sri, 23. 1. 2013 Naslov: Postano: 1:29 sri, 23. 1. 2013 Naslov: |
    |
|
|
Neka je [latex]\{ p_1, p_2, p_3, p_4 \}[/latex] kanonska baza prostora [latex]\mathcal{P}_3[/latex], tj [latex]p_1(t)=1[/latex], [latex]p_2(t)=t[/latex], [latex]p_3(t)=t^2[/latex] i [latex]p_4(t)=t^3[/latex].
Lako (deriviranjem) dobijete
[latex]p_1'(t)=0[/latex], dakle [latex]D(p_1)=\bf{0} [/latex] [latex]\cdot p_1+ [/latex] [latex]\bf{0} [/latex] [latex]\cdot p_2 + [/latex] [latex]\bf{0} [/latex] [latex]\cdot p_3+[/latex] [latex]\bf{0}[/latex] [latex] \cdot p_4[/latex] , te isto i
[latex]p_2'(t)=1[/latex], dakle [latex]D(p_1)=\bf{1} [/latex] [latex]\cdot p_1+ [/latex] [latex]\bf{0} [/latex] [latex]\cdot p_2 + [/latex] [latex]\bf{0} [/latex] [latex]\cdot p_3+[/latex] [latex]\bf{0}[/latex] [latex] \cdot p_4[/latex].
Za [latex]p_3[/latex] i [latex]p_4[/latex] analogno. Boldane brojke stavite u stupce matrice, i eto vam prikaza. Nadam se da je jasnije. Laku noc :)
P.S. Pripazite na eventualne tipfelere, jer je kasno, a nisam provjeravao.
Neka je 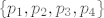 kanonska baza prostora kanonska baza prostora 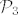 , tj , tj 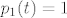 , , 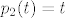 , , 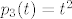 i i 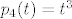 . .
Lako (deriviranjem) dobijete
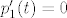 , dakle , dakle 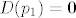 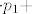 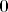 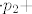 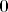 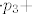 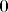 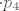 , te isto i , te isto i
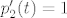 , dakle , dakle 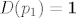 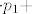 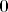 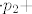 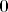 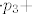 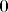 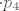 . .
Za 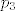 i i 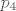 analogno. Boldane brojke stavite u stupce matrice, i eto vam prikaza. Nadam se da je jasnije. Laku noc analogno. Boldane brojke stavite u stupce matrice, i eto vam prikaza. Nadam se da je jasnije. Laku noc 
P.S. Pripazite na eventualne tipfelere, jer je kasno, a nisam provjeravao.
_________________
Luka Zunic
|
|
| [Vrh] |
|
sstudentica
Forumaš(ica)
Pridružen/a: 30. 11. 2010. (13:18:02)
Postovi: (3A)16
|
|
| [Vrh] |
|
|







