| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ivanaaaa
Forumaš(ica)
Pridružen/a: 24. 10. 2011. (19:36:26)
Postovi: (31)16
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
ivanaaaa
Forumaš(ica)
Pridružen/a: 24. 10. 2011. (19:36:26)
Postovi: (31)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 18:27 sri, 10. 4. 2013 Naslov: Postano: 18:27 sri, 10. 4. 2013 Naslov: |
    |
|
|
[quote="goranm"][quote="Nightrider"][quote="goranm"]Kada se pravilno ogranici domena i kodomena pridruzivanja [tex]z\mapsto\sqrt{z}[/tex], onda [tex]\sqrt{zw}=\sqrt z \sqrt w[/tex] ima smisla.[/quote]
Mislim da je maksimalna domena na kojoj ta jednakost vrijedi zapravo nenegativni dio x-osi, svi pozitivni realni brojevi i nula, ispravi me ako sam u krivu.[/quote]
Ako za kodomenu uzmem samo desnu poluravninu bez imaginarne osi (nula ostaje ukljucena), onda je npr. [tex]\sqrt{1\cdot e^{i\pi/4}}=e^{i\pi/8}=\sqrt{1}\cdot\sqrt{e^{i\pi/4}}[/tex].[/quote]
Ja govorim o maksimalnoj domeni, a ne kodomeni, no dobro, uzmi slobodno desnu poluravninu za kodomenu, ali nadji onda domenu(vecu od moje) koja se preslikava u desnu poluravninu, jer bez domene nemas uopce definiranu funkciju.
| goranm (napisa): | | Nightrider (napisa): | | goranm (napisa): | | Kada se pravilno ogranici domena i kodomena pridruzivanja [tex]z\mapsto\sqrt{z}[/tex], onda [tex]\sqrt{zw}=\sqrt z \sqrt w[/tex] ima smisla. |
Mislim da je maksimalna domena na kojoj ta jednakost vrijedi zapravo nenegativni dio x-osi, svi pozitivni realni brojevi i nula, ispravi me ako sam u krivu. |
Ako za kodomenu uzmem samo desnu poluravninu bez imaginarne osi (nula ostaje ukljucena), onda je npr. [tex]\sqrt{1\cdot e^{i\pi/4}}=e^{i\pi/8}=\sqrt{1}\cdot\sqrt{e^{i\pi/4}}[/tex]. |
Ja govorim o maksimalnoj domeni, a ne kodomeni, no dobro, uzmi slobodno desnu poluravninu za kodomenu, ali nadji onda domenu(vecu od moje) koja se preslikava u desnu poluravninu, jer bez domene nemas uopce definiranu funkciju.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 21:23 sri, 10. 4. 2013 Naslov: Postano: 21:23 sri, 10. 4. 2013 Naslov: |
    |
|
|
[quote="Nightrider"][quote="goranm"][quote="Nightrider"][quote="goranm"]Kada se pravilno ogranici domena i kodomena pridruzivanja [tex]z\mapsto\sqrt{z}[/tex], onda [tex]\sqrt{zw}=\sqrt z \sqrt w[/tex] ima smisla.[/quote]
Mislim da je maksimalna domena na kojoj ta jednakost vrijedi zapravo nenegativni dio x-osi, svi pozitivni realni brojevi i nula, ispravi me ako sam u krivu.[/quote]
Ako za kodomenu uzmem samo desnu poluravninu bez imaginarne osi (nula ostaje ukljucena), onda je npr. [tex]\sqrt{1\cdot e^{i\pi/4}}=e^{i\pi/8}=\sqrt{1}\cdot\sqrt{e^{i\pi/4}}[/tex].[/quote]
Ja govorim o maksimalnoj domeni, a ne kodomeni, no dobro, uzmi slobodno desnu poluravninu za kodomenu, ali nadji onda domenu(vecu od moje) koja se preslikava u desnu poluravninu, jer bez domene nemas uopce definiranu funkciju.[/quote]
Pa moja domena je u najmanju ruku isti skup kao i tvoja + jos jedan element, npr. [tex]e^{i \pi/4}[/tex].
Inace, moj komentar koji si citirao glasi "Kada se pravilno ogranici [b]domena i kodomena[/b]", a ne "Kada se uzme maksimalna domena".
| Nightrider (napisa): | | goranm (napisa): | | Nightrider (napisa): | | goranm (napisa): | | Kada se pravilno ogranici domena i kodomena pridruzivanja [tex]z\mapsto\sqrt{z}[/tex], onda [tex]\sqrt{zw}=\sqrt z \sqrt w[/tex] ima smisla. |
Mislim da je maksimalna domena na kojoj ta jednakost vrijedi zapravo nenegativni dio x-osi, svi pozitivni realni brojevi i nula, ispravi me ako sam u krivu. |
Ako za kodomenu uzmem samo desnu poluravninu bez imaginarne osi (nula ostaje ukljucena), onda je npr. [tex]\sqrt{1\cdot e^{i\pi/4}}=e^{i\pi/8}=\sqrt{1}\cdot\sqrt{e^{i\pi/4}}[/tex]. |
Ja govorim o maksimalnoj domeni, a ne kodomeni, no dobro, uzmi slobodno desnu poluravninu za kodomenu, ali nadji onda domenu(vecu od moje) koja se preslikava u desnu poluravninu, jer bez domene nemas uopce definiranu funkciju. |
Pa moja domena je u najmanju ruku isti skup kao i tvoja + jos jedan element, npr. [tex]e^{i \pi/4}[/tex].
Inace, moj komentar koji si citirao glasi "Kada se pravilno ogranici domena i kodomena", a ne "Kada se uzme maksimalna domena".
_________________
The Dude Abides
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 22:34 sri, 10. 4. 2013 Naslov: Postano: 22:34 sri, 10. 4. 2013 Naslov: |
    |
|
|
[quote="Nightrider"]Ovo je pozadina problema: Uzmi kao sto kazes da je tvoja domena moja domena + [latex]e^{i \pi/4}[/latex]. Onda imas: [latex]e^{i \pi/4}[/latex] je u tvojoj domeni, npr. [latex]3[/latex] je u tvojoj domeni(bilo koji realni broj osim 0 i 1 ce radit za ovaj kontraprimjer. I onda imas [latex]\sqrt {2\cdot e^{i \pi/4}}[/latex] nije definirano jer [latex]2\cdot e^{i \pi/4}[/latex] nije u tvojoj domeni.
Shvacas li sad o cemu se radi?[/quote]
Razumio sam i prije o cemu se radi.
[quote] Uzmi kao sto kazes da je tvoja domena moja domena + [latex]e^{i \pi/4}[/latex].[/quote]
Nisam to rekao. Rekao sam "u najmanju ruku", sto je sleng za sadrzi sve te elemente i mozda jos neke (tebi ostavljam da razmislis koji je, uz pripadnu kodomenu, maksimalan podskup ravnine na koji se funkcija moze prosiriti tako da spomenuta jednakost ima smisla). Ali recimo da je to tocno ta domena i neka je A oznaka za nju.
[quote] npr. [latex]3[/latex] je u tvojoj domeni(bilo koji realni broj osim 0 i 1 ce radit za ovaj kontraprimjer. I onda imas [latex]\sqrt {2\cdot e^{i \pi/4}}[/latex] nije definirano jer [latex]2\cdot e^{i \pi/4}[/latex] nije u tvojoj domeni.[/quote]
Zasto bih morao uopce promatrati [latex]2\cdot e^{i \pi/4}[/latex]? Moja funkcija je oblika [tex]A\to B[/tex], ne [tex]A\times A\to B[/tex] i na citavoj domeni spomenuta jedakost ima smisla. Dakle, moram promatrati samo brojeve zw koji su u A, a ne zw td. je (z,w) u AxA. A svaki element iz A mogu rastaviti na produkt elemenata iz A.
| Nightrider (napisa): | Ovo je pozadina problema: Uzmi kao sto kazes da je tvoja domena moja domena + 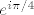 . Onda imas: . Onda imas: 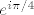 je u tvojoj domeni, npr. je u tvojoj domeni, npr. 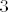 je u tvojoj domeni(bilo koji realni broj osim 0 i 1 ce radit za ovaj kontraprimjer. I onda imas je u tvojoj domeni(bilo koji realni broj osim 0 i 1 ce radit za ovaj kontraprimjer. I onda imas 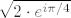 nije definirano jer nije definirano jer 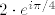 nije u tvojoj domeni. nije u tvojoj domeni.
Shvacas li sad o cemu se radi? |
Razumio sam i prije o cemu se radi.
| Citat: | Uzmi kao sto kazes da je tvoja domena moja domena + 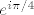 . . |
Nisam to rekao. Rekao sam "u najmanju ruku", sto je sleng za sadrzi sve te elemente i mozda jos neke (tebi ostavljam da razmislis koji je, uz pripadnu kodomenu, maksimalan podskup ravnine na koji se funkcija moze prosiriti tako da spomenuta jednakost ima smisla). Ali recimo da je to tocno ta domena i neka je A oznaka za nju.
| Citat: | npr. 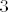 je u tvojoj domeni(bilo koji realni broj osim 0 i 1 ce radit za ovaj kontraprimjer. I onda imas je u tvojoj domeni(bilo koji realni broj osim 0 i 1 ce radit za ovaj kontraprimjer. I onda imas 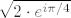 nije definirano jer nije definirano jer 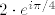 nije u tvojoj domeni. nije u tvojoj domeni. |
Zasto bih morao uopce promatrati 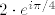 ? Moja funkcija je oblika [tex]A\to B[/tex], ne [tex]A\times A\to B[/tex] i na citavoj domeni spomenuta jedakost ima smisla. Dakle, moram promatrati samo brojeve zw koji su u A, a ne zw td. je (z,w) u AxA. A svaki element iz A mogu rastaviti na produkt elemenata iz A. ? Moja funkcija je oblika [tex]A\to B[/tex], ne [tex]A\times A\to B[/tex] i na citavoj domeni spomenuta jedakost ima smisla. Dakle, moram promatrati samo brojeve zw koji su u A, a ne zw td. je (z,w) u AxA. A svaki element iz A mogu rastaviti na produkt elemenata iz A.
_________________
The Dude Abides
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 22:48 sri, 10. 4. 2013 Naslov: Postano: 22:48 sri, 10. 4. 2013 Naslov: |
    |
|
|
[quote="goranm"]Zasto bih morao uopce promatrati [latex]2\cdot e^{i \pi/4}[/latex]? Moja funkcija je oblika [tex]A\to B[/tex], ne [tex]A\times A\to B[/tex] i na citavoj domeni spomenuta jedakost ima smisla. Dakle, moram promatrati samo brojeve zw koji su u A, a ne u AxA. A svaki element iz A mogu rastaviti na produkt elemenata iz A.[/quote]
Tu se razilazimo u misljenjima, funkcija "drugi korijen" stvarno djeluje sa nekog A na neki B ([tex]A\to B[/tex]) no ja smatram da moras promatrat upravo podskupove od [tex]\mathbb C \times \mathbb C[/tex] da bi dosao do podrucja vrijednosti na kojem je izraz [tex]f(z,w)={\sqrt{z \cdot w}}={\sqrt{z}} \cdot {\sqrt{w}}[/tex] valjan jer lijeva strana uzima dva kompleksna broja.
EDIT: Moguce je da ces svaki element iz A moci rastavit na produkt elemenata iz A no tesko da ce produkt svaka dva elementa iz A lezat u A. U tome je bit.
| goranm (napisa): | Zasto bih morao uopce promatrati 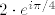 ? Moja funkcija je oblika [tex]A\to B[/tex], ne [tex]A\times A\to B[/tex] i na citavoj domeni spomenuta jedakost ima smisla. Dakle, moram promatrati samo brojeve zw koji su u A, a ne u AxA. A svaki element iz A mogu rastaviti na produkt elemenata iz A. ? Moja funkcija je oblika [tex]A\to B[/tex], ne [tex]A\times A\to B[/tex] i na citavoj domeni spomenuta jedakost ima smisla. Dakle, moram promatrati samo brojeve zw koji su u A, a ne u AxA. A svaki element iz A mogu rastaviti na produkt elemenata iz A. |
Tu se razilazimo u misljenjima, funkcija "drugi korijen" stvarno djeluje sa nekog A na neki B ([tex]A\to B[/tex]) no ja smatram da moras promatrat upravo podskupove od [tex]\mathbb C \times \mathbb C[/tex] da bi dosao do podrucja vrijednosti na kojem je izraz [tex]f(z,w)={\sqrt{z \cdot w}}={\sqrt{z}} \cdot {\sqrt{w}}[/tex] valjan jer lijeva strana uzima dva kompleksna broja.
EDIT: Moguce je da ces svaki element iz A moci rastavit na produkt elemenata iz A no tesko da ce produkt svaka dva elementa iz A lezat u A. U tome je bit.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 23:04 sri, 10. 4. 2013 Naslov: Postano: 23:04 sri, 10. 4. 2013 Naslov: |
    |
|
|
[quote="Nightrider"]
Tu se razilazimo u misljenjima, funkcija "drugi korijen" stvarno djeluje sa nekog A na neki B ([tex]A\to B[/tex]) no ja smatram da moras promatrat upravo podskupove od [tex]\mathbb C \times \mathbb C[/tex] da bi dosao do podrucja vrijednosti na kojem je izraz [tex]f(z,w)={\sqrt{z \cdot w}}={\sqrt{z}} \cdot {\sqrt{w}}[/tex] valjan jer lijeva strana uzima dva kompleksna broja.[/quote]
Nije to stvar misljenja. Ako je pitanje "da li svojstvo S vrijedi za funkciju [tex]f\colon X\to Y[/tex]", onda odgovor "ne, jer svojstvo S ne vrijedi za funkciju [tex]g\colon X\times X\to Y[/tex]" u ovom slucaju nije valjan argument.
[quote]EDIT: Moguce je da ces svaki element iz A moci rastavit na produkt elemenata iz A no tesko da ce produkt svaka dva elementa iz A lezat u A. U tome je bit.[/quote]
Nije. Bit je da prosirenje postoji. Mene ne zanima algebarska struktura koju mogu dobiti iz skupa A, nego da li za funkciju [tex]\sqrt{\hspace{.2cm}} \colon A\to B[/tex] vrijedi [tex]\sqrt{zw}=\sqrt z \sqrt w[/tex].
| Nightrider (napisa): |
Tu se razilazimo u misljenjima, funkcija "drugi korijen" stvarno djeluje sa nekog A na neki B ([tex]A\to B[/tex]) no ja smatram da moras promatrat upravo podskupove od [tex]\mathbb C \times \mathbb C[/tex] da bi dosao do podrucja vrijednosti na kojem je izraz [tex]f(z,w)={\sqrt{z \cdot w}}={\sqrt{z}} \cdot {\sqrt{w}}[/tex] valjan jer lijeva strana uzima dva kompleksna broja. |
Nije to stvar misljenja. Ako je pitanje "da li svojstvo S vrijedi za funkciju [tex]f\colon X\to Y[/tex]", onda odgovor "ne, jer svojstvo S ne vrijedi za funkciju [tex]g\colon X\times X\to Y[/tex]" u ovom slucaju nije valjan argument.
| Citat: | | EDIT: Moguce je da ces svaki element iz A moci rastavit na produkt elemenata iz A no tesko da ce produkt svaka dva elementa iz A lezat u A. U tome je bit. |
Nije. Bit je da prosirenje postoji. Mene ne zanima algebarska struktura koju mogu dobiti iz skupa A, nego da li za funkciju [tex]\sqrt{\hspace{.2cm}} \colon A\to B[/tex] vrijedi [tex]\sqrt{zw}=\sqrt z \sqrt w[/tex].
_________________
The Dude Abides
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 23:19 sri, 10. 4. 2013 Naslov: Postano: 23:19 sri, 10. 4. 2013 Naslov: |
    |
|
|
[quote="goranm"]Nije to stvar misljenja. Ako je pitanje "da li svojstvo S vrijedi za funkciju [tex]f\colon X\to Y[/tex]", onda odgovor "ne, jer svojstvo S ne vrijedi za funkciju [tex]g\colon X\times X\to Y[/tex]" u ovom slucaju nije valjan argument.[/quote]
Nije to ni bio moj argument.
[quote="goranm"]Nije. Bit je da prosirenje postoji. Mene ne zanima algebarska struktura koju mogu dobiti iz skupa A, nego da li za funkciju [tex]\sqrt{\hspace{.2cm}} \colon A\to B[/tex] vrijedi [tex]\sqrt{zw}=\sqrt z \sqrt w[/tex].[/quote]
Meni izgleda da prosirenje, u smislu da ono sadrzi cijeli nenegativni dio x-osi i jos dodatne elemente, ne postoji. Svaki skup koji ja uzmem za prosirenje nije zatvoren s obzirom na mnozenje kompleksnih brojeva, mozda si ciljao na krug radijusa 1 no ni on u uniji sa nenegativnim dijelom x-osi nije zatvoren s obzirom na mnozenje( a mnozenje je s lijeve strane pod znakom korijena):
| goranm (napisa): | | Nije to stvar misljenja. Ako je pitanje "da li svojstvo S vrijedi za funkciju [tex]f\colon X\to Y[/tex]", onda odgovor "ne, jer svojstvo S ne vrijedi za funkciju [tex]g\colon X\times X\to Y[/tex]" u ovom slucaju nije valjan argument. |
Nije to ni bio moj argument.
| goranm (napisa): | | Nije. Bit je da prosirenje postoji. Mene ne zanima algebarska struktura koju mogu dobiti iz skupa A, nego da li za funkciju [tex]\sqrt{\hspace{.2cm}} \colon A\to B[/tex] vrijedi [tex]\sqrt{zw}=\sqrt z \sqrt w[/tex]. |
Meni izgleda da prosirenje, u smislu da ono sadrzi cijeli nenegativni dio x-osi i jos dodatne elemente, ne postoji. Svaki skup koji ja uzmem za prosirenje nije zatvoren s obzirom na mnozenje kompleksnih brojeva, mozda si ciljao na krug radijusa 1 no ni on u uniji sa nenegativnim dijelom x-osi nije zatvoren s obzirom na mnozenje( a mnozenje je s lijeve strane pod znakom korijena):
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 23:30 sri, 10. 4. 2013 Naslov: Postano: 23:30 sri, 10. 4. 2013 Naslov: |
    |
|
|
[quote="Nightrider"]Nije to ni bio moj argument.[/quote]
Kako nije kada si malo prije upravo to napisao.
[quote]
Meni izgleda da prosirenje, u smislu da ono sadrzi cijeli nenegativni dio x-osi i jos dodatne elemente, ne postoji.[/quote]
Ako ogranicis kodomenu, onda prosirenje postoji, sto sam i demonstrirao maloprije.
[quote]Svaki skup koji ja uzmem za prosirenje nije zatvoren s obzirom na mnozenje kompleksnih brojeva, mozda si ciljao na krug radijusa 1 no ni on u uniji sa nenegativnim dijelom x-osi nije zatvoren s obzirom na mnozenje( a mnozenje je s lijeve strane pod znakom korijena):[/quote]
Zasto bi trebalo biti zatvoreno na mnozenje? Ne interesira me da li je [tex](A,\cdot)[/tex] magma (grupoid), nego da li jednakost vrijedi na A.
| Nightrider (napisa): | | Nije to ni bio moj argument. |
Kako nije kada si malo prije upravo to napisao.
| Citat: |
Meni izgleda da prosirenje, u smislu da ono sadrzi cijeli nenegativni dio x-osi i jos dodatne elemente, ne postoji. |
Ako ogranicis kodomenu, onda prosirenje postoji, sto sam i demonstrirao maloprije.
| Citat: | | Svaki skup koji ja uzmem za prosirenje nije zatvoren s obzirom na mnozenje kompleksnih brojeva, mozda si ciljao na krug radijusa 1 no ni on u uniji sa nenegativnim dijelom x-osi nije zatvoren s obzirom na mnozenje( a mnozenje je s lijeve strane pod znakom korijena): |
Zasto bi trebalo biti zatvoreno na mnozenje? Ne interesira me da li je [tex](A,\cdot)[/tex] magma (grupoid), nego da li jednakost vrijedi na A.
_________________
The Dude Abides
|
|
| [Vrh] |
|
|















