| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 20:55 ned, 7. 4. 2013 Naslov: U potrazi za kombinatornim objasnjenjem Postano: 20:55 ned, 7. 4. 2013 Naslov: U potrazi za kombinatornim objasnjenjem |
    |
|
|
Pretpostavljam da ovo nikoga ne zanima, no nije steta postavit jos jedno pitanje.
Imamo ovu "igru". U kutiji su dvi kuglice, jedna zelena i jedna zuta. Vjerojatnost da izvucemo zutu je [latex]1/2[/latex], i vjerojatnost da izvucemo zelenu je isto [latex]1/2[/latex]. Ako nakon prvog izvlacenja izvucemo zelenu igra je gotova, ako izvucemo zutu vracamo ju u kutiju i stavljamo jos jednu zutu kuglicu u kutiju,. Izvlacimo drugi put. Sada je vjerojatnost da izvucemo zelenu [latex]1/3[/latex] a da izvucemo zutu [latex]2/3[/latex]. Opet, ako se izvuce zelena igra je gotova, ako izvucemo zutu vracamo ju u kutiju i dodajemo jos jednu zutu kuglicu u kutiju, nastavljajuci na ovaj nacin, kad izvlacimo [latex]n[/latex]-ti put imamo [latex](n+1)[/latex]-u kuglicu u kutiji, [latex]n[/latex] zutih i jednu zelenu, s vjerojatnoscu [latex]\frac {1}{n+1}[/latex] da ce izvucena kuglica biti zelena i vjerojatnoscu [latex]\frac {n}{n+1}[/latex] da ce izvucena kuglica biti zuta.
Ako se sad zapitamo kolika je vjerojatnost da [b]do[/b] [latex]k[/latex]-tog izvlacenja zavrsi igra (ukljucujuci [latex]k[/latex]-to u ovome "[b]do[/b]") to se lako moze odgovorit:
Oznacimo sa [latex]P(A=k)[/latex] dogadjaj "[b]u[/b] [latex]k[/latex]-tom izvlacenju izvucena je zelena kuglica". Pitanje je dakle, vrijednost od [latex]P(A\leq k)[/latex]. Prvo imamo [latex]P(A\leq k)=\sum_{i=1}^k P(A=i)[/latex]. Pa se problem svodi na nalazenje vrijednosti od [latex]P(A=i)[/latex], sto je vjerojatnost da je [b]u[/b] [latex]i[/latex]-tom izvlacenju izvucena zelena kuglica, no [b]u[/b] [latex]i[/latex]-tom izvlacenju izvucena je zelena kuglica ako i samo ako je u prvih [latex](i-1)[/latex] izvlacenja izvucena zuta i [b]u[/b] [latex]i[/latex]-tom izvlacenju je izvucena zelena. Zbog nezavisnosti dogadjaja imamo [latex]P(A=i)={\frac {1}{2}}\cdot {\frac {2}{3}}\cdot {\frac {3}{4}}\cdot ... \cdot {\frac {i-1}{i}\cdot {\frac {1}{i+1}={\frac {1}{i(i+1)}}[/latex]. Time se dobije [latex]P(A\leq k)=\sum_{i=1}^k P(A=i)=\sum_{i=1}^k {\frac {1}{i(i+1)}=\sum_{i=1}^k ({\frac {1}{i}}-{\frac {1}{i+1}})=1-{\frac {1}{k+1}}={\frac {k}{k+1}}[/latex].
Sad se vidi da je vjerojatnost da [b]do[/b] [latex]k[/latex]-tog izvlacenja izvucemo zelenu kuglicu (tojest da ju izvucemo ili u prvom ili u drugom ili...ili u [latex]k[/latex]-tom izvlacenju) zapravo jednaka vjerojatnosti da [b]u[/b] [latex]k[/latex]-tom izvlacenju izvucemo zutu kuglicu, i to je na neki sebi svojstven nacin zanimljiv rezultat.
Pa se nekako samo po sebi namece pitanje, kako cisto kombinatornim argumentima opravdati ovaj rezultat?
Ako netko ima ideju kako bi se ovo moglo kombinatorno interpretirat nek se osjeca slobodno da mi napise ovdje.
Ako nema ideju neka mi smanji sarmu da me obeshrabri u postavljanju ovakvih pitanja.
Pretpostavljam da ovo nikoga ne zanima, no nije steta postavit jos jedno pitanje.
Imamo ovu "igru". U kutiji su dvi kuglice, jedna zelena i jedna zuta. Vjerojatnost da izvucemo zutu je 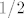 , i vjerojatnost da izvucemo zelenu je isto , i vjerojatnost da izvucemo zelenu je isto 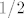 . Ako nakon prvog izvlacenja izvucemo zelenu igra je gotova, ako izvucemo zutu vracamo ju u kutiju i stavljamo jos jednu zutu kuglicu u kutiju,. Izvlacimo drugi put. Sada je vjerojatnost da izvucemo zelenu . Ako nakon prvog izvlacenja izvucemo zelenu igra je gotova, ako izvucemo zutu vracamo ju u kutiju i stavljamo jos jednu zutu kuglicu u kutiju,. Izvlacimo drugi put. Sada je vjerojatnost da izvucemo zelenu 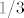 a da izvucemo zutu a da izvucemo zutu 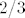 . Opet, ako se izvuce zelena igra je gotova, ako izvucemo zutu vracamo ju u kutiju i dodajemo jos jednu zutu kuglicu u kutiju, nastavljajuci na ovaj nacin, kad izvlacimo . Opet, ako se izvuce zelena igra je gotova, ako izvucemo zutu vracamo ju u kutiju i dodajemo jos jednu zutu kuglicu u kutiju, nastavljajuci na ovaj nacin, kad izvlacimo  -ti put imamo -ti put imamo  -u kuglicu u kutiji, -u kuglicu u kutiji,  zutih i jednu zelenu, s vjerojatnoscu zutih i jednu zelenu, s vjerojatnoscu 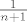 da ce izvucena kuglica biti zelena i vjerojatnoscu da ce izvucena kuglica biti zelena i vjerojatnoscu 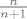 da ce izvucena kuglica biti zuta. da ce izvucena kuglica biti zuta.
Ako se sad zapitamo kolika je vjerojatnost da do  -tog izvlacenja zavrsi igra (ukljucujuci -tog izvlacenja zavrsi igra (ukljucujuci  -to u ovome "do") to se lako moze odgovorit: -to u ovome "do") to se lako moze odgovorit:
Oznacimo sa 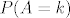 dogadjaj "u dogadjaj "u  -tom izvlacenju izvucena je zelena kuglica". Pitanje je dakle, vrijednost od -tom izvlacenju izvucena je zelena kuglica". Pitanje je dakle, vrijednost od  . Prvo imamo . Prvo imamo 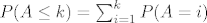 . Pa se problem svodi na nalazenje vrijednosti od . Pa se problem svodi na nalazenje vrijednosti od 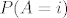 , sto je vjerojatnost da je u , sto je vjerojatnost da je u  -tom izvlacenju izvucena zelena kuglica, no u -tom izvlacenju izvucena zelena kuglica, no u  -tom izvlacenju izvucena je zelena kuglica ako i samo ako je u prvih -tom izvlacenju izvucena je zelena kuglica ako i samo ako je u prvih  izvlacenja izvucena zuta i u izvlacenja izvucena zuta i u  -tom izvlacenju je izvucena zelena. Zbog nezavisnosti dogadjaja imamo -tom izvlacenju je izvucena zelena. Zbog nezavisnosti dogadjaja imamo 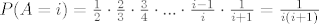 . Time se dobije . Time se dobije 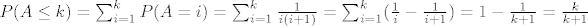 . .
Sad se vidi da je vjerojatnost da do  -tog izvlacenja izvucemo zelenu kuglicu (tojest da ju izvucemo ili u prvom ili u drugom ili...ili u -tog izvlacenja izvucemo zelenu kuglicu (tojest da ju izvucemo ili u prvom ili u drugom ili...ili u  -tom izvlacenju) zapravo jednaka vjerojatnosti da u -tom izvlacenju) zapravo jednaka vjerojatnosti da u  -tom izvlacenju izvucemo zutu kuglicu, i to je na neki sebi svojstven nacin zanimljiv rezultat. -tom izvlacenju izvucemo zutu kuglicu, i to je na neki sebi svojstven nacin zanimljiv rezultat.
Pa se nekako samo po sebi namece pitanje, kako cisto kombinatornim argumentima opravdati ovaj rezultat?
Ako netko ima ideju kako bi se ovo moglo kombinatorno interpretirat nek se osjeca slobodno da mi napise ovdje.
Ako nema ideju neka mi smanji sarmu da me obeshrabri u postavljanju ovakvih pitanja.
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 11:23 sri, 10. 4. 2013 Naslov: Postano: 11:23 sri, 10. 4. 2013 Naslov: |
    |
|
|
[quote="nana"]Nisi bas to dobro skombinirao.
Vjerojatnost da je izvucena zelena kuglica u k-tom izvacenju podrazumjeva da nije izvucena u prethodnih k-1 izvlacenja
inace A=k je podskup od A<=k
a iz jednakosti vjerojatnosti(koje si zakljucio) to bi impliciralo da je P(A<=k-1)=0
p.s. A je slucajna varijabla pa je uobicajeno oznacit sa slovom X,Y,Z itd (s kraja abecede)[/quote]
Bacio sam jos jednom pogled i sve mi izgleda dobro, jedino sta sam se zabunio kad sam napisao "oznacimo sa[latex]P(A=k)[/latex] dogadjaj "u k-tom izvlacenju izvucena je zelena kuglica"" dok sam zapravo mislio (a to je kasnije sasvim jasno iz racuna) napisat "oznacimo sa "[latex]P(A=k)[/latex] vjerojatnost dogadjaja "u k-tom izvlacenju izvucena je zelena kuglica"". Isto se vidi da sam sa [latex]P(A\leq k)[/latex] oznacio dogadjaj "ili u prvom ili u drugom ili... ili u k-tom izvlacenju izvucena je zelena kuglica"(pa je princip zbrajanja vjerojatnosti dopusten jer se radi o disjunktnim dogadjajima).
[color=violet]Duso[/color], nije mi jasno to sta kazes: "a iz jednakosti vjerojatnosti(koje si zakljucio) to bi impliciralo da je [latex]P(A\leq k-1)=0[/latex]".
Nebi. Zasto? Zato sta je dobiven rezultat da je vjerojatnost da je ili u prvom ili u drugom ili... ili u k-tom izvlacenju izvucena [color=green]zelena[/color] kuglica jednaka vjerojatnosti da je u k-tom izvlacenju izvucena [color=yellow]zuta[/color] kuglica.
Tako da, ako si mislila sa izjavom [latex]P(A\leq k-1)=0[/latex] oznacit ovaj proces [latex]P(A\leq k)-P(A=k)[/latex] onda si pobrkala vjerojatnost da je izvucena zuta kuglica u k-tom izvlacenju sa vjerojatnoscu da je izvucena zelena kuglica u k-tom izvlacenju.
Zasto? Zato sta bi ovo [latex]P(A\leq k)-P(A=k)[/latex] (u tvojoj opaski, ako sam razumio sta mi zelis kazat) znacilo oduzimanje vjerojatnosti vezane uz zelenu kuglicu koja ukljucuje k-to izvlacenje od vjerojatnosti vezane uz zutu kuglicu koja ukljucuje k-to izvlacenje, a to je nedopustivo jer bi u istom trenu u ovom procesu ukljucila dogadjaj "izvucena je zuta kuglica" i "izvucena je zelena kuglica" a oni su, gledajuci jedno te isto, fiksno izvlacenje, prvo, uzajamno iskljucivi, drugo, nemogu se dogodit u istom izvlacenju.
Ajmo oznacit(premda nema potrebe) sa [latex]P(B=k)[/latex] vjerojatnost da je u k-tom izvlacenju izvucena zuta kuglica. Onda ovaj rezultat govori da je [latex]P(A\leq k)=P(B=k)[/latex] a ne da je [latex]P(A\leq k)=P(A=k)[/latex].
Jel sad jasnije?
| nana (napisa): | Nisi bas to dobro skombinirao.
Vjerojatnost da je izvucena zelena kuglica u k-tom izvacenju podrazumjeva da nije izvucena u prethodnih k-1 izvlacenja
inace A=k je podskup od A⇐k
a iz jednakosti vjerojatnosti(koje si zakljucio) to bi impliciralo da je P(A⇐k-1)=0
p.s. A je slucajna varijabla pa je uobicajeno oznacit sa slovom X,Y,Z itd (s kraja abecede) |
Bacio sam jos jednom pogled i sve mi izgleda dobro, jedino sta sam se zabunio kad sam napisao "oznacimo sa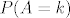 dogadjaj "u k-tom izvlacenju izvucena je zelena kuglica"" dok sam zapravo mislio (a to je kasnije sasvim jasno iz racuna) napisat "oznacimo sa " dogadjaj "u k-tom izvlacenju izvucena je zelena kuglica"" dok sam zapravo mislio (a to je kasnije sasvim jasno iz racuna) napisat "oznacimo sa "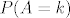 vjerojatnost dogadjaja "u k-tom izvlacenju izvucena je zelena kuglica"". Isto se vidi da sam sa vjerojatnost dogadjaja "u k-tom izvlacenju izvucena je zelena kuglica"". Isto se vidi da sam sa  oznacio dogadjaj "ili u prvom ili u drugom ili... ili u k-tom izvlacenju izvucena je zelena kuglica"(pa je princip zbrajanja vjerojatnosti dopusten jer se radi o disjunktnim dogadjajima). oznacio dogadjaj "ili u prvom ili u drugom ili... ili u k-tom izvlacenju izvucena je zelena kuglica"(pa je princip zbrajanja vjerojatnosti dopusten jer se radi o disjunktnim dogadjajima).
Duso, nije mi jasno to sta kazes: "a iz jednakosti vjerojatnosti(koje si zakljucio) to bi impliciralo da je 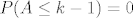 ". ".
Nebi. Zasto? Zato sta je dobiven rezultat da je vjerojatnost da je ili u prvom ili u drugom ili... ili u k-tom izvlacenju izvucena zelena kuglica jednaka vjerojatnosti da je u k-tom izvlacenju izvucena zuta kuglica.
Tako da, ako si mislila sa izjavom 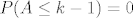 oznacit ovaj proces oznacit ovaj proces  onda si pobrkala vjerojatnost da je izvucena zuta kuglica u k-tom izvlacenju sa vjerojatnoscu da je izvucena zelena kuglica u k-tom izvlacenju. onda si pobrkala vjerojatnost da je izvucena zuta kuglica u k-tom izvlacenju sa vjerojatnoscu da je izvucena zelena kuglica u k-tom izvlacenju.
Zasto? Zato sta bi ovo  (u tvojoj opaski, ako sam razumio sta mi zelis kazat) znacilo oduzimanje vjerojatnosti vezane uz zelenu kuglicu koja ukljucuje k-to izvlacenje od vjerojatnosti vezane uz zutu kuglicu koja ukljucuje k-to izvlacenje, a to je nedopustivo jer bi u istom trenu u ovom procesu ukljucila dogadjaj "izvucena je zuta kuglica" i "izvucena je zelena kuglica" a oni su, gledajuci jedno te isto, fiksno izvlacenje, prvo, uzajamno iskljucivi, drugo, nemogu se dogodit u istom izvlacenju. (u tvojoj opaski, ako sam razumio sta mi zelis kazat) znacilo oduzimanje vjerojatnosti vezane uz zelenu kuglicu koja ukljucuje k-to izvlacenje od vjerojatnosti vezane uz zutu kuglicu koja ukljucuje k-to izvlacenje, a to je nedopustivo jer bi u istom trenu u ovom procesu ukljucila dogadjaj "izvucena je zuta kuglica" i "izvucena je zelena kuglica" a oni su, gledajuci jedno te isto, fiksno izvlacenje, prvo, uzajamno iskljucivi, drugo, nemogu se dogodit u istom izvlacenju.
Ajmo oznacit(premda nema potrebe) sa 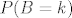 vjerojatnost da je u k-tom izvlacenju izvucena zuta kuglica. Onda ovaj rezultat govori da je vjerojatnost da je u k-tom izvlacenju izvucena zuta kuglica. Onda ovaj rezultat govori da je 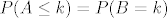 a ne da je a ne da je 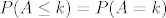 . .
Jel sad jasnije?
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 15:16 sri, 10. 4. 2013 Naslov: Postano: 15:16 sri, 10. 4. 2013 Naslov: |
    |
|
|
[quote="nana"]zutozeleno pocinje na z. isprika :D[/quote]
[b]Z[/b]asto ja ne vidim zgodno kombinatorno objasnjenje pocinje sa [b]z[/b]. Kako god okrenes recenicu.
[quote="nana"]al opet mi se cini da vjerojatnost n/(n+1) je zapravo P(izabrana je ZUTA| u prethodnih n je izabrana ZUTA)[/quote]
Samo ti se cini da je nesto neispravno, sve je u redu. Razumijem i tu primjedbu, ti gledas na to kao ako u n-tom izvlacenju izvucemo zutu onda smo morali izvuci zutu i u prvih (n-1) izvlacenja jer bi u protivnom igra zavrsila pa bi vjerojatnost izvlacenja zute trebala biti manja a ja na n-to izvlacenje gledam kao na izolirano izvlacenje u smislu, kao: Gle, dosli smo do n-tog izvlacenja, sad mozemo izvlacit kuglice, vjerojatnost da izvucemo zutu je n/(n+1). Tako da mozda ali samo mozda treba unijeti jos dodatne preciznosti u problem ali svakako, primjedba ti je veoma dobra i konstruktivna.
[quote="nana"]Sretno s kombinatornim objasnjenjem 8)[/quote]
Oh, well, thank you! Ne brigaj se, kad sam bio mali zvali su me Pascalov Trokut. 8)
DODATAK: Taj tvoj nacin gledanja na problem, kad malo promotrim, je jednako dobar, no on takodjer sa sobom povlaci potrebu za kombinatornim objasnjenjem jer on daje rezultat da je vjerojatnost da je zuta kuglica izvucena u k-tom izvlacenju(uz pretpostavku ovisnosti o prethodnim izvlacenjima) jednaka vjerojatnosti da je zelena kuglica izvucena u k-tom izvlacenju. Tako da imamo ovo:
Moja verzija(promatram k-to izvlacenje kao izolirano(neovisno) od ostalih): Objasni kombinatorno da je vjerojatnost da je zelena kuglica izvucena ili u prvom ili u drugom ili...ili u k-tom izvlacenju jednaka vjerojatnosti da je zuta kuglica izvucena u k-tom izvlacenju.
Tvoja verzija(promatras k-to izvlacenje kao ovisno o ostalim): Objasni kombinatorno da je vjerojatnost izvlacenja zute kuglice u k-tom izvlacenju jednaka vjerojatnosti izvlacenja zelene kuglice u k-tom izvlacenju.
Dobro, u svakom slucaju, dala si novu dimenziju problemu tako da u ovisnosti o nacinu gledanja na k-to izvlacenje zute kuglice imamo dva problema, oba nas mole da ih kombinatorno objasnimo.
| nana (napisa): | zutozeleno pocinje na z. isprika  |
Zasto ja ne vidim zgodno kombinatorno objasnjenje pocinje sa z. Kako god okrenes recenicu.
| nana (napisa): | | al opet mi se cini da vjerojatnost n/(n+1) je zapravo P(izabrana je ZUTA| u prethodnih n je izabrana ZUTA) |
Samo ti se cini da je nesto neispravno, sve je u redu. Razumijem i tu primjedbu, ti gledas na to kao ako u n-tom izvlacenju izvucemo zutu onda smo morali izvuci zutu i u prvih (n-1) izvlacenja jer bi u protivnom igra zavrsila pa bi vjerojatnost izvlacenja zute trebala biti manja a ja na n-to izvlacenje gledam kao na izolirano izvlacenje u smislu, kao: Gle, dosli smo do n-tog izvlacenja, sad mozemo izvlacit kuglice, vjerojatnost da izvucemo zutu je n/(n+1). Tako da mozda ali samo mozda treba unijeti jos dodatne preciznosti u problem ali svakako, primjedba ti je veoma dobra i konstruktivna.
| nana (napisa): | Sretno s kombinatornim objasnjenjem  |
Oh, well, thank you! Ne brigaj se, kad sam bio mali zvali su me Pascalov Trokut. 
DODATAK: Taj tvoj nacin gledanja na problem, kad malo promotrim, je jednako dobar, no on takodjer sa sobom povlaci potrebu za kombinatornim objasnjenjem jer on daje rezultat da je vjerojatnost da je zuta kuglica izvucena u k-tom izvlacenju(uz pretpostavku ovisnosti o prethodnim izvlacenjima) jednaka vjerojatnosti da je zelena kuglica izvucena u k-tom izvlacenju. Tako da imamo ovo:
Moja verzija(promatram k-to izvlacenje kao izolirano(neovisno) od ostalih): Objasni kombinatorno da je vjerojatnost da je zelena kuglica izvucena ili u prvom ili u drugom ili...ili u k-tom izvlacenju jednaka vjerojatnosti da je zuta kuglica izvucena u k-tom izvlacenju.
Tvoja verzija(promatras k-to izvlacenje kao ovisno o ostalim): Objasni kombinatorno da je vjerojatnost izvlacenja zute kuglice u k-tom izvlacenju jednaka vjerojatnosti izvlacenja zelene kuglice u k-tom izvlacenju.
Dobro, u svakom slucaju, dala si novu dimenziju problemu tako da u ovisnosti o nacinu gledanja na k-to izvlacenje zute kuglice imamo dva problema, oba nas mole da ih kombinatorno objasnimo.
|
|
| [Vrh] |
|
|








