| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)

Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
 Postano: 13:12 čet, 21. 3. 2013 Naslov: Re: Vježba za 1 kolokvij Postano: 13:12 čet, 21. 3. 2013 Naslov: Re: Vježba za 1 kolokvij |
    |
|
|
[quote="pedro"]http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij1.pdf
može 1. zad pod a)
nacrtala sam sliku i sad me dalje muči kako bih odredila granice integriranja[/quote]
Rješavanjem jednadžbe [tex]a(1+cos\phi) = a[/tex] dobiješ da se kružnica i kardioida sjeku u samo dvije točke, za [tex]\phi = 0[/tex] te za [tex]\phi = \pi[/tex]. To znači da je kružnica u potpunosti sadržana unutar kardioide.
Dakle, za riješiti zadatak je dosta izračunati površinu unutar kardioide i oduzeti površinu kružnice. Površinu kružnice znaš, iznosi [tex]a^2\pi[/tex], jedino trebaš izračunati površinu unutar kardioide. Za to je najprirodnije okružje polarne koordinate, treba integrirati Jacobijan polarnih koordinata, tj. r, u granicama zadanima u zadatku.
Granice za polarne koordinate dolaze posve prirodno, [tex]\phi[/tex] se kreće od [tex]0[/tex] do [tex]2\pi[/tex], dok se [tex]r[/tex] kreće od [tex]0[/tex] do kardioide, dakle do [tex]1+cos\phi[/tex].
| pedro (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij1.pdf
može 1. zad pod a)
nacrtala sam sliku i sad me dalje muči kako bih odredila granice integriranja |
Rješavanjem jednadžbe [tex]a(1+cos\phi) = a[/tex] dobiješ da se kružnica i kardioida sjeku u samo dvije točke, za [tex]\phi = 0[/tex] te za [tex]\phi = \pi[/tex]. To znači da je kružnica u potpunosti sadržana unutar kardioide.
Dakle, za riješiti zadatak je dosta izračunati površinu unutar kardioide i oduzeti površinu kružnice. Površinu kružnice znaš, iznosi [tex]a^2\pi[/tex], jedino trebaš izračunati površinu unutar kardioide. Za to je najprirodnije okružje polarne koordinate, treba integrirati Jacobijan polarnih koordinata, tj. r, u granicama zadanima u zadatku.
Granice za polarne koordinate dolaze posve prirodno, [tex]\phi[/tex] se kreće od [tex]0[/tex] do [tex]2\pi[/tex], dok se [tex]r[/tex] kreće od [tex]0[/tex] do kardioide, dakle do [tex]1+cos\phi[/tex].
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)

Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
 Postano: 13:56 čet, 21. 3. 2013 Naslov: Postano: 13:56 čet, 21. 3. 2013 Naslov: |
    |
|
|
Jer imaju samo dvije dodirne točke. Sa skice je jasno da te dvije dodirne točke postoje svakako. A sad, da kružnica i izlazi iz kardioide, morale bi postojati dodatne točke presjeka, i to barem još četiri zbog simetrije krivulja s obzirom na x-os.
Drugim riječima, da bi kružnica ulazila i izlazila iz kardioide, dosta su dvije točke presjeka. Međutim, sa skice je jasno da je nemoguće da kružnica izlazi na tim mjestima, dakle trebaju nam neke druge točke presjeka.
I da, druga granica integracije je [tex]a(1+cos\phi)[/tex]
Jer imaju samo dvije dodirne točke. Sa skice je jasno da te dvije dodirne točke postoje svakako. A sad, da kružnica i izlazi iz kardioide, morale bi postojati dodatne točke presjeka, i to barem još četiri zbog simetrije krivulja s obzirom na x-os.
Drugim riječima, da bi kružnica ulazila i izlazila iz kardioide, dosta su dvije točke presjeka. Međutim, sa skice je jasno da je nemoguće da kružnica izlazi na tim mjestima, dakle trebaju nam neke druge točke presjeka.
I da, druga granica integracije je [tex]a(1+cos\phi)[/tex]
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 14:29 čet, 21. 3. 2013 Naslov: Postano: 14:29 čet, 21. 3. 2013 Naslov: |
    |
|
|
Hvala!
[size=9][color=#999999]Added after 24 seconds:[/color][/size]
[quote="pedro"]http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij1.pdf
može 6 zad[/quote]
može i 4??
[size=9][color=#999999]Added after 26 minutes:[/color][/size]
[quote="fkirsek"]Jer imaju samo dvije dodirne točke. Sa skice je jasno da te dvije dodirne točke postoje svakako. A sad, da kružnica i izlazi iz kardioide, morale bi postojati dodatne točke presjeka, i to barem još četiri zbog simetrije krivulja s obzirom na x-os.
Drugim riječima, da bi kružnica ulazila i izlazila iz kardioide, dosta su dvije točke presjeka. Međutim, sa skice je jasno da je nemoguće da kružnica izlazi na tim mjestima, dakle trebaju nam neke druge točke presjeka.
I da, druga granica integracije je [tex]a(1+cos\phi)[/tex][/quote]
dobila sam rješenje a^2PI
Hvala!
Added after 24 seconds:
| pedro (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij1.pdf
može 6 zad |
može i 4??
Added after 26 minutes:
| fkirsek (napisa): | Jer imaju samo dvije dodirne točke. Sa skice je jasno da te dvije dodirne točke postoje svakako. A sad, da kružnica i izlazi iz kardioide, morale bi postojati dodatne točke presjeka, i to barem još četiri zbog simetrije krivulja s obzirom na x-os.
Drugim riječima, da bi kružnica ulazila i izlazila iz kardioide, dosta su dvije točke presjeka. Međutim, sa skice je jasno da je nemoguće da kružnica izlazi na tim mjestima, dakle trebaju nam neke druge točke presjeka.
I da, druga granica integracije je [tex]a(1+cos\phi)[/tex] |
dobila sam rješenje a^2PI
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 14:33 čet, 21. 3. 2013 Naslov: Re: Vježba za 1 kolokvij Postano: 14:33 čet, 21. 3. 2013 Naslov: Re: Vježba za 1 kolokvij |
    |
|
|
[quote="fkirsek"]
Rješavanjem jednadžbe [tex]a(1+cos\phi) = a[/tex] dobiješ da se kružnica i kardioida sjeku u samo dvije točke, za [tex]\phi = 0[/tex] te za [tex]\phi = \pi[/tex].[/quote]
[strike]sijeku se u 4 tocke, i krivu si jednadzbu postavio.[/strike]
[quote="fkirsek"]To znači da je kružnica u potpunosti sadržana unutar kardioide.[/quote]
[strike], ima dijelova gdje je kardioida izvan kruznice i dijelova gdje je kruznica izvan kardioide.[/strike]
[quote="fkirsek"] za polarne koordinate dolaze posve prirodno, [tex]\phi[/tex] se kreće od [tex]0[/tex] do [tex]2\pi[/tex][/quote],
[strike], zasto bi granice uvijek isle od [latex]0[/latex] do [latex]2\pi[/latex]?[/strike]
[quote="fkirsek"] se [tex]r[/tex] kreće od [tex]0[/tex] do kardioide, dakle do [tex]1+cos\phi[/tex].[/quote]
[strike] prvo u problemu uopce nisu potrebne vrijednosti od
[latex]r[/latex] u kojima se sijeku kruznica i kardioida jer je [latex]r[/latex] funkcija od [latex]\phi[/latex] pa u integraciju ne ulazi [latex]r[/latex] a i da ulazi granica mu ne bi bila [latex]1+cos\phi[/latex] [/strike]
| fkirsek (napisa): |
Rješavanjem jednadžbe [tex]a(1+cos\phi) = a[/tex] dobiješ da se kružnica i kardioida sjeku u samo dvije točke, za [tex]\phi = 0[/tex] te za [tex]\phi = \pi[/tex]. |
sijeku se u 4 tocke, i krivu si jednadzbu postavio.
| fkirsek (napisa): | | To znači da je kružnica u potpunosti sadržana unutar kardioide. |
, ima dijelova gdje je kardioida izvan kruznice i dijelova gdje je kruznica izvan kardioide.
| fkirsek (napisa): | | za polarne koordinate dolaze posve prirodno, [tex]\phi[/tex] se kreće od [tex]0[/tex] do [tex]2\pi[/tex] |
,
, zasto bi granice uvijek isle od  do do 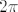 ? ?
| fkirsek (napisa): | | se [tex]r[/tex] kreće od [tex]0[/tex] do kardioide, dakle do [tex]1+cos\phi[/tex]. |
prvo u problemu uopce nisu potrebne vrijednosti od
 u kojima se sijeku kruznica i kardioida jer je u kojima se sijeku kruznica i kardioida jer je  funkcija od funkcija od 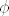 pa u integraciju ne ulazi pa u integraciju ne ulazi  a i da ulazi granica mu ne bi bila a i da ulazi granica mu ne bi bila 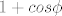
Zadnja promjena: Nightrider; 18:37 sub, 30. 3. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)

Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
 Postano: 15:57 čet, 21. 3. 2013 Naslov: Re: Vježba za 1 kolokvij Postano: 15:57 čet, 21. 3. 2013 Naslov: Re: Vježba za 1 kolokvij |
    |
|
|
[quote="Nightrider"]
Krivo, sijeku se u 4 tocke, i krivu si jednadzbu postavio.
[/quote]
Greškom sam postavio krivu jednadžbu, ali se ipak sjeku samo u dvije točke.
[quote="Nightrider"]
Krivo, zasto bi granice uvijek isle od [latex]0[/latex] do [latex]2\pi[/latex]?
[/quote]
Nisam nigdje rekao da su uvijek te granice, ali u ovom zadatku nam baš te trebaju.
[quote="Nightrider"]
Krivo, prvo u problemu uopce nisu potrebne vrijednosti od
[latex]r[/latex] u kojima se sijeku kruznica i kardioida jer je [latex]r[/latex] funkcija od [latex]\phi[/latex] pa u integraciju ne ulazi [latex]r[/latex] a i da ulazi granica mu ne bi bila [latex]1+cos\phi[/latex][/quote]
A inače nikad uvrštavamo funkcije od [tex]\phi[/tex]-ja kao granice integracije? :?
Svakako ćeš morati koristiti granice kardioide i već sam se ispravio da nisu [tex]1+cos\phi[/tex] već [latex]a(1+cos\phi)[/latex]
Ispričavam se, zbog brzine pišem gluposti.
Dakle, ovaj put nadam se ispravno rješenje :oops:
Parametrizacija kardioide:
[tex]
x = r cos \phi = acos\phi(1+cos\phi)\\
y = r sin \phi = asin\phi(1+cos\phi)
[/tex]
[tex]
(x-a)^2 + y^2 = a^2\\
(r cos\phi - a)^2 + (r sin\phi)^2 = a^2\\
r^2 cos^2\phi - 2arcos\phi + a^2 + r^2 sin^2 \phi = a^2\\
r^2 - 2arcos\phi = 0\\
r(r - 2acos\phi = 0
[/tex]
1. slučaj
[tex]
r = 0
[/tex]
iz jednadžbe kardioide uvrstimo r
[tex]
a(1+cos\phi)=0\\
a + acos\phi = 0\\
acos\phi = -a\\
cos\phi = -1\\
\phi = \pi\\
[/tex]
2. slučaj
[tex]
r - 2acos\phi = 0\\
r = 2acos\phi
[/tex]
iz jednadžbe kardioide uvrstimo r
[tex]
a+acos\phi = 2acos\phi\\
cos\phi = 1\\
\phi = 0
[/tex]
Dakle kružnica je zaista sadržana u kardioidi i ostatak rješenja je točno. Meni integral ispada [tex]\frac{3}{2}a^2\pi[/tex], dakle to umanjeno za površinu kruga je [tex]\frac{1}{2}a^2\pi[/tex]
| Nightrider (napisa): |
Krivo, sijeku se u 4 tocke, i krivu si jednadzbu postavio.
|
Greškom sam postavio krivu jednadžbu, ali se ipak sjeku samo u dvije točke.
| Nightrider (napisa): |
Krivo, zasto bi granice uvijek isle od  do do 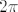 ? ?
|
Nisam nigdje rekao da su uvijek te granice, ali u ovom zadatku nam baš te trebaju.
| Nightrider (napisa): |
Krivo, prvo u problemu uopce nisu potrebne vrijednosti od
 u kojima se sijeku kruznica i kardioida jer je u kojima se sijeku kruznica i kardioida jer je  funkcija od funkcija od 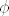 pa u integraciju ne ulazi pa u integraciju ne ulazi  a i da ulazi granica mu ne bi bila a i da ulazi granica mu ne bi bila 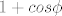 |
A inače nikad uvrštavamo funkcije od [tex]\phi[/tex]-ja kao granice integracije? 
Svakako ćeš morati koristiti granice kardioide i već sam se ispravio da nisu [tex]1+cos\phi[/tex] već 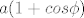
Ispričavam se, zbog brzine pišem gluposti.
Dakle, ovaj put nadam se ispravno rješenje 
Parametrizacija kardioide:
[tex]
x = r cos \phi = acos\phi(1+cos\phi)\\
y = r sin \phi = asin\phi(1+cos\phi)
[/tex]
[tex]
(x-a)^2 + y^2 = a^2\\
(r cos\phi - a)^2 + (r sin\phi)^2 = a^2\\
r^2 cos^2\phi - 2arcos\phi + a^2 + r^2 sin^2 \phi = a^2\\
r^2 - 2arcos\phi = 0\\
r(r - 2acos\phi = 0
[/tex]
1. slučaj
[tex]
r = 0
[/tex]
iz jednadžbe kardioide uvrstimo r
[tex]
a(1+cos\phi)=0\\
a + acos\phi = 0\\
acos\phi = -a\\
cos\phi = -1\\
\phi = \pi\\
[/tex]
2. slučaj
[tex]
r - 2acos\phi = 0\\
r = 2acos\phi
[/tex]
iz jednadžbe kardioide uvrstimo r
[tex]
a+acos\phi = 2acos\phi\\
cos\phi = 1\\
\phi = 0
[/tex]
Dakle kružnica je zaista sadržana u kardioidi i ostatak rješenja je točno. Meni integral ispada [tex]\frac{3}{2}a^2\pi[/tex], dakle to umanjeno za površinu kruga je [tex]\frac{1}{2}a^2\pi[/tex]
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 16:19 čet, 21. 3. 2013 Naslov: Re: Vježba za 1 kolokvij Postano: 16:19 čet, 21. 3. 2013 Naslov: Re: Vježba za 1 kolokvij |
    |
|
|
[quote="fkirsek"][quote="Nightrider"]
Krivo, sijeku se u 4 tocke, i krivu si jednadzbu postavio.[/quote]
Greškom sam postavio krivu jednadžbu, ali se ipak sjeku samo u dvije točke.
[/quote]
Cini mi se da si ipak u pravu, sad kad plottam i meni izgleda tako, neznam sto sam iscrtao prvi put kad sam tvrdio da se sijeku u 4, no slika sad i mene uvjerava da su 2. ovo je graf za a=2.
http://www.wolframalpha.com/input/?i=polar+plot+r%3D2%281%2Bcos+theta%29+and+r%3D4cos+theta
[quote="fkirsek"]
Ispričavam se, zbog brzine pišem gluposti.[/quote]
Takodjer, ja pisem jos vece gluposti.
| fkirsek (napisa): | | Nightrider (napisa): |
Krivo, sijeku se u 4 tocke, i krivu si jednadzbu postavio. |
Greškom sam postavio krivu jednadžbu, ali se ipak sjeku samo u dvije točke.
|
Cini mi se da si ipak u pravu, sad kad plottam i meni izgleda tako, neznam sto sam iscrtao prvi put kad sam tvrdio da se sijeku u 4, no slika sad i mene uvjerava da su 2. ovo je graf za a=2.
http://www.wolframalpha.com/input/?i=polar+plot+r%3D2%281%2Bcos+theta%29+and+r%3D4cos+theta
| fkirsek (napisa): |
Ispričavam se, zbog brzine pišem gluposti. |
Takodjer, ja pisem jos vece gluposti.
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)

Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
 Postano: 17:54 čet, 21. 3. 2013 Naslov: Postano: 17:54 čet, 21. 3. 2013 Naslov: |
    |
|
|
[quote="pedro"]2 zadatak:
zanima me jesi li dobre granice??
[latex]\int_{0}^{2\pi }\int_{0}^{\pi -\frac{1}{2}x} (x-2y)^{2}sin(x+2y)dy dx[/latex]
i zna netko to sad rješit?[/quote]
Dobre su granice integracije.
Najlakše je integral riješiti zamjenom varijabli, i to najprirodnijom:
[tex]
u = x+2y\\
v = x-2y\\
[/tex]
iz čega se dobije
[tex]
x = \frac{1}{2}(u+v)\\
y = \frac{1}{4}(u-v)\\
[/tex]
Jacobijan tog preslikavanja je [tex]\frac{1}{4}[/tex], a integral postaje
[tex]\int v^2 sin (u) du dv[/tex]. Jedino je pitanje koje su granice integracije. Pravac [tex]y = \pi - \frac{1}{2}x[/tex] se može napisati kao [tex]x+y = 2\pi[/tex] što je upravo [tex]u = 2\pi[/tex]. Dakle [tex]u[/tex] možemo staviti da ide od [tex]0[/tex] do [tex]2\pi[/tex].
Sada treba koordinatne osi prikazati u ovim koordinatama. Pošto smo u uzeli za slobodnu, v trebamo prikazati koristeći u.
x-os je pravac [tex]y = 0[/tex], uvrštavajući to u jednadžbe za u i v dobijamo
[tex]
u = x\\
v = x\\
[/tex], dakle x-os je pravac [tex]v=u[/tex]. Slično se dobije da je y-os pravac [tex]v = -u[/tex]. Dakle granice integracije za v su [tex]-u[/tex] do [tex]u[/tex].
Sve ukupno se dobije
[tex]
\frac{1}{4}\int_0^{2\pi} ( \int_{-u}^{u} v^2 sin(u) dv) du
[/tex]
[size=9][color=#999999]Added after 38 minutes:[/color][/size]
4. zadatak od iste godine:
Dakle, pitanje je ima li skup [tex]L(C )[/tex] površinu. Koristit ćemo teorem o zamjeni varijabli (iako možemo koristiti i Korolar 9.5 koji će isti rezultat dati izravno). Prvo, primjetimo da je L regularna matrica, tj. da će determinanta preslikavanja L(x,y) biti različita od nule. Prema teoremu o zamjeni varijabli (ili Korolaru 9.5) dobijamo da, ako [tex]C[/tex] ima površinu, onda i [tex]L(C)[/tex] ima površinu i ta površina je upravo [tex] |det L|\nu(C) [/tex].
Štoviše, pošto je [tex]L[/tex] regularan, postoji inverzno preslikavanje [tex]L^{-1}[/tex], pa vrijedi i obrnuto, ako skup [tex]L(C)[/tex] ima površinu, onda ju ima i skup [tex]C[/tex]. Obratom po kontrapoziciji dobijemo: ako skup [tex]C[/tex] nema površinu, nema je ni skup [tex]L(C)[/tex].
Ukratko, vrijedi:
[tex]L(C)[/tex] ima površinu ako i samo ako skup [tex]C[/tex] ima površinu.
Dakle, trebamo to provjeriti samo za skup [tex]C[/tex]. Skup [tex]C[/tex]. će imati površinu ako je ograničen i ako mu je rub skup mjere nula.
Je li skup [tex]C[/tex] ograničen? Da! Lako se pokaže (vidi sa grafa, ako ništa drugo) da je taj skup sadržan u pravokutniku čiji su rubovi točke [tex](0,0), (0,3), (1,0), (1,3)[/tex], dakle ograničen je.
Je li rub skupa mjere nula?
Također je jasno da je rub skupa unija tri dužine (koje su mjere nula) i grafa funkcije [tex]f(x) = \frac{1}{1+x}[/tex] na segmentu [tex][0,3][/tex].
Znamo da vrijedi da je graf neprekidne funkcije na segmentu mjere nula. Gornja funkcija je zaista takva pa je njen graf mjere nula. Dakle rub skupa [tex]C[/tex] je konačna unija skupova mjere nula, pa je i sam mjere nula.
Dakle [tex]C[/tex] ima površinu, pa površinu ima i [tex]L(C)[/tex].
[size=9][color=#999999]Added after 28 minutes:[/color][/size]
6. zadatak od iste godine:
a)
Intuitivno gledano, oscilacija funkcije je najveći mogući "skok" funkcije u toj točki. Za funkciju
[tex]\frac{xy}{x^2+y^2}[/tex] vjerojatno nije jasno u ovom obliku koliki je taj najveći skok, no jasno je da postoji pošto funkcija nije neprekidna u [tex]0[/tex]. Naime, ako se nuli približavamo po x-osi ili y-osi, limes je 0, dok ako se krećemo po pravcima x = y ili x = -y, limes ispada [tex]\frac{1}{2}[/tex] tj. [tex]\frac{-1}{2}[/tex]. Ovdje se već da naslutiti da je oscilacija barem 1.
Formalnije, lakše je funkciju promatrati u polarnim koordinatama. Poznatom supstitucijom
[tex]
x = r cos \phi\\
y = r sin \phi\\
[/tex]
naša funkcija poprima oblik
[tex]
f(x,y) = f(r cos \phi ,r sin \phi) = \frac{rcos\phi rsin\phi}{r^2cos^2\phi + r^2 sin^2 \phi}\\
= \frac{r^2sin\phi cos\phi}{r^2} = sin\phi cos\phi = \frac{1}{2}sin(2\phi)[/tex]
Iz ovoga je jasno da funkcija f ne ovisi o radijusu r, dakle u bilo kojoj okolini ishodišta je moguće pronaći sve vrijednosti funkcije f.
Također slijedi da je, pošto je funkcija f zapravo [tex] \frac{1}{2}sin(2\phi)[/tex] tj. u osnovi sinus, jnjen maksimum [tex] \frac{1}{2}[/tex], a minimum [tex] \frac{-1}{2}[/tex].
Taj maksimum i minimum je moguće postići na bilo kojoj otvorenoj okolini ishodišta, dakle na svakoj okolini [tex]U[/tex] je
[tex]sup_{x_1,x_2 \in U \cap \mathbb{R}^2} |f(x_1) - f(x_2)| = 1[/tex], pošto je to razlika maksimuma i minimuma. Iz toga slijedi da je oscilacija infimum jednočlanog skupa [tex]\{1\}[/tex], pa je oscilacija tog skupa upravo 1.
b)
f je ovdje karakteristična funkcija skupa, dakle poprima vrijednost 1 ako se točka nalazi na kružnici, a 0 ako se ne nalazi. Pošto ta kružnica prolazi kroz ishodište te pošto je kružnica skup mjere nula, a nijedan neprazan otvoren skup nije mjere 0, svaka otvorena okolina ishodišta mora sadržavati i točke iz kružnice, i točke izvan kružnice.
Trivijalno je da je maksimum funkcije upravo 1, a minimum 0.
Iz svega toga slijedi da se maksimum i minimum postižu na svakoj okolini ishodišta, pa je opet njihova razlika upravo oscilacija.
Dakle, oscilacija je 1.
| pedro (napisa): | 2 zadatak:
zanima me jesi li dobre granice??
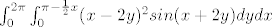
i zna netko to sad rješit? |
Dobre su granice integracije.
Najlakše je integral riješiti zamjenom varijabli, i to najprirodnijom:
[tex]
u = x+2y\\
v = x-2y\\
[/tex]
iz čega se dobije
[tex]
x = \frac{1}{2}(u+v)\\
y = \frac{1}{4}(u-v)\\
[/tex]
Jacobijan tog preslikavanja je [tex]\frac{1}{4}[/tex], a integral postaje
[tex]\int v^2 sin (u) du dv[/tex]. Jedino je pitanje koje su granice integracije. Pravac [tex]y = \pi - \frac{1}{2}x[/tex] se može napisati kao [tex]x+y = 2\pi[/tex] što je upravo [tex]u = 2\pi[/tex]. Dakle [tex]u[/tex] možemo staviti da ide od [tex]0[/tex] do [tex]2\pi[/tex].
Sada treba koordinatne osi prikazati u ovim koordinatama. Pošto smo u uzeli za slobodnu, v trebamo prikazati koristeći u.
x-os je pravac [tex]y = 0[/tex], uvrštavajući to u jednadžbe za u i v dobijamo
[tex]
u = x\\
v = x\\
[/tex], dakle x-os je pravac [tex]v=u[/tex]. Slično se dobije da je y-os pravac [tex]v = -u[/tex]. Dakle granice integracije za v su [tex]-u[/tex] do [tex]u[/tex].
Sve ukupno se dobije
[tex]
\frac{1}{4}\int_0^{2\pi} ( \int_{-u}^{u} v^2 sin(u) dv) du
[/tex]
Added after 38 minutes:
4. zadatak od iste godine:
Dakle, pitanje je ima li skup [tex]L(C )[/tex] površinu. Koristit ćemo teorem o zamjeni varijabli (iako možemo koristiti i Korolar 9.5 koji će isti rezultat dati izravno). Prvo, primjetimo da je L regularna matrica, tj. da će determinanta preslikavanja L(x,y) biti različita od nule. Prema teoremu o zamjeni varijabli (ili Korolaru 9.5) dobijamo da, ako [tex]C[/tex] ima površinu, onda i [tex]L(C)[/tex] ima površinu i ta površina je upravo [tex] |det L|\nu(C) [/tex].
Štoviše, pošto je [tex]L[/tex] regularan, postoji inverzno preslikavanje [tex]L^{-1}[/tex], pa vrijedi i obrnuto, ako skup [tex]L(C)[/tex] ima površinu, onda ju ima i skup [tex]C[/tex]. Obratom po kontrapoziciji dobijemo: ako skup [tex]C[/tex] nema površinu, nema je ni skup [tex]L(C)[/tex].
Ukratko, vrijedi:
[tex]L(C)[/tex] ima površinu ako i samo ako skup [tex]C[/tex] ima površinu.
Dakle, trebamo to provjeriti samo za skup [tex]C[/tex]. Skup [tex]C[/tex]. će imati površinu ako je ograničen i ako mu je rub skup mjere nula.
Je li skup [tex]C[/tex] ograničen? Da! Lako se pokaže (vidi sa grafa, ako ništa drugo) da je taj skup sadržan u pravokutniku čiji su rubovi točke [tex](0,0), (0,3), (1,0), (1,3)[/tex], dakle ograničen je.
Je li rub skupa mjere nula?
Također je jasno da je rub skupa unija tri dužine (koje su mjere nula) i grafa funkcije [tex]f(x) = \frac{1}{1+x}[/tex] na segmentu [tex][0,3][/tex].
Znamo da vrijedi da je graf neprekidne funkcije na segmentu mjere nula. Gornja funkcija je zaista takva pa je njen graf mjere nula. Dakle rub skupa [tex]C[/tex] je konačna unija skupova mjere nula, pa je i sam mjere nula.
Dakle [tex]C[/tex] ima površinu, pa površinu ima i [tex]L(C)[/tex].
Added after 28 minutes:
6. zadatak od iste godine:
a)
Intuitivno gledano, oscilacija funkcije je najveći mogući "skok" funkcije u toj točki. Za funkciju
[tex]\frac{xy}{x^2+y^2}[/tex] vjerojatno nije jasno u ovom obliku koliki je taj najveći skok, no jasno je da postoji pošto funkcija nije neprekidna u [tex]0[/tex]. Naime, ako se nuli približavamo po x-osi ili y-osi, limes je 0, dok ako se krećemo po pravcima x = y ili x = -y, limes ispada [tex]\frac{1}{2}[/tex] tj. [tex]\frac{-1}{2}[/tex]. Ovdje se već da naslutiti da je oscilacija barem 1.
Formalnije, lakše je funkciju promatrati u polarnim koordinatama. Poznatom supstitucijom
[tex]
x = r cos \phi\\
y = r sin \phi\\
[/tex]
naša funkcija poprima oblik
[tex]
f(x,y) = f(r cos \phi ,r sin \phi) = \frac{rcos\phi rsin\phi}{r^2cos^2\phi + r^2 sin^2 \phi}\\
= \frac{r^2sin\phi cos\phi}{r^2} = sin\phi cos\phi = \frac{1}{2}sin(2\phi)[/tex]
Iz ovoga je jasno da funkcija f ne ovisi o radijusu r, dakle u bilo kojoj okolini ishodišta je moguće pronaći sve vrijednosti funkcije f.
Također slijedi da je, pošto je funkcija f zapravo [tex] \frac{1}{2}sin(2\phi)[/tex] tj. u osnovi sinus, jnjen maksimum [tex] \frac{1}{2}[/tex], a minimum [tex] \frac{-1}{2}[/tex].
Taj maksimum i minimum je moguće postići na bilo kojoj otvorenoj okolini ishodišta, dakle na svakoj okolini [tex]U[/tex] je
[tex]sup_{x_1,x_2 \in U \cap \mathbb{R}^2} |f(x_1) - f(x_2)| = 1[/tex], pošto je to razlika maksimuma i minimuma. Iz toga slijedi da je oscilacija infimum jednočlanog skupa [tex]\{1\}[/tex], pa je oscilacija tog skupa upravo 1.
b)
f je ovdje karakteristična funkcija skupa, dakle poprima vrijednost 1 ako se točka nalazi na kružnici, a 0 ako se ne nalazi. Pošto ta kružnica prolazi kroz ishodište te pošto je kružnica skup mjere nula, a nijedan neprazan otvoren skup nije mjere 0, svaka otvorena okolina ishodišta mora sadržavati i točke iz kružnice, i točke izvan kružnice.
Trivijalno je da je maksimum funkcije upravo 1, a minimum 0.
Iz svega toga slijedi da se maksimum i minimum postižu na svakoj okolini ishodišta, pa je opet njihova razlika upravo oscilacija.
Dakle, oscilacija je 1.
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)

Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
 Postano: 18:18 čet, 21. 3. 2013 Naslov: Postano: 18:18 čet, 21. 3. 2013 Naslov: |
    |
|
|
Mali dodatak na prošli post, na 6. zadatak
Tek sam sad shvatio da se pitaju oscilacije u SVAKOJ točki :D
Pa, za a) dio zadatka nije problem, trivijalno se pokaže da je funkcija neprekidna u svakoj točki osim u 0, pa je u svim drugim točkama oscilacija 0.
U b) dijelu su prekidi u svim točkama kružnice i za sve te točke vrijedi ista analiza koju sam napravio za ishodište - dakle oscilacija je 1 na toj kružnici, a 0 van te kružnice.
[size=9][color=#999999]Added after 16 minutes:[/color][/size]
5. zadatak dakle.
a) Odgovor je DA! Naime, [tex]\bar{C}=C \cup \partial C[/tex]. Tj. rub skupa [tex]\bar{C}[/tex] je upravo [tex]\partial C[/tex].
Jednostavna posljedica Lebesguevogo teorema (navedena u Napomeni 6.8 ) je da ograničen skup ima površinu akko njegov rub ima površinu nula.
Pošto [tex]C[/tex] ima površinu, njegov rub je površine nula, dakle i rub od [tex]\bar{C}[/tex] ima površinu nula. Nadalje, [tex]\bar{C}[/tex] je unija dvaju ograničenih skupova, pa je i sam ograničen skup. Dakle [tex]\bar{C}[/tex] ima površinu.
b) Da. Iz gornje analize slijedi da skup [tex]\bar{C}[/tex] ima površinu. Nadalje, njegova površina je ograničena zbrojom površina od [tex]C[/tex] i [tex]\partial C[/tex], pošto je taj skup jednak [tex]\bar{C}=C \cup \partial C[/tex] (jednakost bi vrijedila kad bi znali da su skupovi [tex]C[/tex] i [tex]\partial C[/tex] disjunktni).
No, kao i gore, rub od [tex]C[/tex] je površine nula, iz uvjeta je i [tex]C[/tex] površine nula, pa je i [tex]\bar{C}[/tex] površine nula.
c) Da. Najjednostavniji primjer skupa koji nema površinu, a mjere je nula, je [tex]\mathbb{Q^2}\cap [0,1]\times[0,1]\subset \mathbb{R}^2[/tex]. Pokazali ste, a i prilično je intuitivno, zašto taj skup nema površinu. Također, trivijalno je da je taj skup ograničen.
No, zatvarač tog skupa je upravo [tex][0,1]^2[/tex], tj. jedinični kvadrat, a taj skup ima površinu (cijela ideja površine bi bila vrlo čudna da nema :D)
Mali dodatak na prošli post, na 6. zadatak
Tek sam sad shvatio da se pitaju oscilacije u SVAKOJ točki 
Pa, za a) dio zadatka nije problem, trivijalno se pokaže da je funkcija neprekidna u svakoj točki osim u 0, pa je u svim drugim točkama oscilacija 0.
U b) dijelu su prekidi u svim točkama kružnice i za sve te točke vrijedi ista analiza koju sam napravio za ishodište - dakle oscilacija je 1 na toj kružnici, a 0 van te kružnice.
Added after 16 minutes:
5. zadatak dakle.
a) Odgovor je DA! Naime, [tex]\bar{C}=C \cup \partial C[/tex]. Tj. rub skupa [tex]\bar{C}[/tex] je upravo [tex]\partial C[/tex].
Jednostavna posljedica Lebesguevogo teorema (navedena u Napomeni 6.8 ) je da ograničen skup ima površinu akko njegov rub ima površinu nula.
Pošto [tex]C[/tex] ima površinu, njegov rub je površine nula, dakle i rub od [tex]\bar{C}[/tex] ima površinu nula. Nadalje, [tex]\bar{C}[/tex] je unija dvaju ograničenih skupova, pa je i sam ograničen skup. Dakle [tex]\bar{C}[/tex] ima površinu.
b) Da. Iz gornje analize slijedi da skup [tex]\bar{C}[/tex] ima površinu. Nadalje, njegova površina je ograničena zbrojom površina od [tex]C[/tex] i [tex]\partial C[/tex], pošto je taj skup jednak [tex]\bar{C}=C \cup \partial C[/tex] (jednakost bi vrijedila kad bi znali da su skupovi [tex]C[/tex] i [tex]\partial C[/tex] disjunktni).
No, kao i gore, rub od [tex]C[/tex] je površine nula, iz uvjeta je i [tex]C[/tex] površine nula, pa je i [tex]\bar{C}[/tex] površine nula.
c) Da. Najjednostavniji primjer skupa koji nema površinu, a mjere je nula, je [tex]\mathbb{Q^2}\cap [0,1]\times[0,1]\subset \mathbb{R}^2[/tex]. Pokazali ste, a i prilično je intuitivno, zašto taj skup nema površinu. Također, trivijalno je da je taj skup ograničen.
No, zatvarač tog skupa je upravo [tex][0,1]^2[/tex], tj. jedinični kvadrat, a taj skup ima površinu (cijela ideja površine bi bila vrlo čudna da nema  ) )
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)

Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)

Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
 Postano: 18:48 čet, 21. 3. 2013 Naslov: Postano: 18:48 čet, 21. 3. 2013 Naslov: |
    |
|
|
Za pravce x = 0 i y = 0:
jer su oni rub tog skupa. I u tvom integralu su se pojavili x = 0 i y = 0 kao granice integracije.
Za 1. b)
Pošto smo u 3D, radi se o volumenu tetraedra. Tetraedar je piramida, a volumen piramide je [tex]\frac{1}{3} * P(baza) * visina[/tex]. Baza je pravokutnik, visina je upravo jedna stranica (pošto je kut između te stranice i baze 90°. Dakle volumen je 6.
Nadalje, za granicu z-a moraš uzeti funkciju koja opisuje gornju ravninu. Ta ravnina će ovisiti o x i o y. Postoji više načina za pronalaženje jednadžbe ravnine, najlakše je segmentnim oblikom
[tex] \frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1[/tex]
Dakle, granica za z je [tex]0[/tex] do [tex]3 - 3x -\frac{3y}{2} [/tex], a granica za y ti NIJE
[tex]\frac{-x}{2} + 2[/tex] već [tex]-2x + 2[/tex]. To najlakše vidiš ako promatraš samo xy ravninu, dakle zanemariš ovisnost o z-u.
[size=9][color=#999999]Added after 7 minutes:[/color][/size]
[quote="pedro"]
jesi rješio možda integral? dobila sam 5pi/3[/quote]
Koji točno integral?
Najlbrže provjeriš integrale na WA.
[url=http://www.wolframalpha.com/input/?i=double+integrate&f1=%28x-2y%29%5E2sin%28x%2B2y%29&f=DoubleIntegral.integrand_%28x-2y%29%5E2sin%28x%2B2y%29&f2=x&f=DoubleIntegral.intvariable1_x&f3=0&f=DoubleIntegral.rangestart1_0&f4=2pi&f=DoubleIntegral.rangeend1_2pi&f5=y&f=DoubleIntegral.intvariable2_y&f6=0&f=DoubleIntegral.rangestart2_0&f7=pi+-+1%2F2x&f=DoubleIntegral.rangeend2_pi+-+1%2F2x]npr. ovako[/url] ili
[url=http://www.wolframalpha.com/input/?i=double+integrate&f1=v%5E2+sin%28u%29&f=DoubleIntegral.integrand_v%5E2+sin%28u%29&f2=u&f=DoubleIntegral.intvariable1_u&f3=0&f=DoubleIntegral.rangestart1_0&f4=2pi&f=DoubleIntegral.rangeend1_2pi&f5=v&f=DoubleIntegral.intvariable2_v&f6=-u&f=DoubleIntegral.rangestart2_-u&f7=u&f=DoubleIntegral.rangeend2_u] ovako [/url]
Za pravce x = 0 i y = 0:
jer su oni rub tog skupa. I u tvom integralu su se pojavili x = 0 i y = 0 kao granice integracije.
Za 1. b)
Pošto smo u 3D, radi se o volumenu tetraedra. Tetraedar je piramida, a volumen piramide je [tex]\frac{1}{3} * P(baza) * visina[/tex]. Baza je pravokutnik, visina je upravo jedna stranica (pošto je kut između te stranice i baze 90°. Dakle volumen je 6.
Nadalje, za granicu z-a moraš uzeti funkciju koja opisuje gornju ravninu. Ta ravnina će ovisiti o x i o y. Postoji više načina za pronalaženje jednadžbe ravnine, najlakše je segmentnim oblikom
[tex] \frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1[/tex]
Dakle, granica za z je [tex]0[/tex] do [tex]3 - 3x -\frac{3y}{2} [/tex], a granica za y ti NIJE
[tex]\frac{-x}{2} + 2[/tex] već [tex]-2x + 2[/tex]. To najlakše vidiš ako promatraš samo xy ravninu, dakle zanemariš ovisnost o z-u.
Added after 7 minutes:
| pedro (napisa): |
jesi rješio možda integral? dobila sam 5pi/3 |
Koji točno integral?
Najlbrže provjeriš integrale na WA.
npr. ovako ili
ovako
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)

Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
|






