|
3.15 d)
Ovaj kosinus u brojniku poprima samo konačno mnogo vijednosti: i to samo -1, 1 i 0. Kada si raspišemo prvih par članova dobijemo:
[latex] \frac{1}{\sqrt{2}} \cdot ( \frac{-1}{\sqrt{1}} + \frac{1}{\sqrt{2}} + \frac{-1}{\sqrt{3}} + \frac{1}{\sqrt{4}} + ... ) [/latex]
Ovaj red unutar zagrada po leibnitzu konvergira, ali po integralnom apsolutno ne konvergira.
A grupa:
Primijetimo da je [latex] \sqrt{n^3+1} - \sqrt{n^3} =\frac{1}{\sqrt{n^3+1} + \sqrt{n^3}} [/latex], što teži u nulu kad n ide u beskonačnost.
Zato po usporednom kriteriju (smijemo ga lupati jer su sigurno svi članovi pozitivni), početni red konvergira ako i samo ako konvergira red kojemu su članovi [latex] \sqrt{n^3+1} - \sqrt{n^3} =\frac{1}{\sqrt{n^3+1} + \sqrt{n^3}} [/latex], a to opet po usporednom kriteriju konvergira ako i samo ako konvergira red kojemu su članovi [latex] \frac{1}{\sqrt{n^3}} [/latex]. Ovaj zadnji red znamo da konvergira, integralni kriterij (eksponent mu je 1.5).
B grupa (a slično ide u i D):
Da bi dokazali konvergenciju, lupit ćemo leibnitzov kriterij, no zato trebamo pokazati da su svi izrazi [latex] \frac{1}{\sqrt{n}} \cdot sin (\frac{1}{1+\sqrt{n}}) [/latex] pozitivni i da su padajući. Očito su pozitivni (jer su argumenti sinusa u intervalu 0 do pipola). Padajućost ćemo dokazati deriviranjem: definiramo si funkciju [latex] f(x) = \frac{1}{x} \cdot sin (\frac{1}{1+x}) [/latex]. Njena derivacija je negativna, pa je funkcija padajuća, pa je i niz padajuć. Joj, da, trebamo pokazati i da niz teži u nulu, no to je također očito.
D: grupa:
Opet si definiramo funkciju, [latex] f(x)= x * sin^2 (\frac{1}{x}) [/latex]. Njena derivacija je [latex] sin (\frac{1}{x}) \cdot ( sin (\frac{1}{x}) - \frac{ 2 cos (\frac{1}{x})}{x}) [/latex]. Za nju nije tako očito da je manja od nule, pa ću malo više argumentirati. Naime, za [latex] x>3/\pi [/latex] vrijedi da je [latex]cos(\frac{1}{x}) > \frac{1}{2}[/latex], pa je za takve ikseve [latex] sin (\frac{1}{x}) - \frac{ 2 cos (\frac{1}{x})}{x} < sin (\frac{1}{x}) - \frac{1}{x} <0 [/latex] (zadnja nejednakost slijedi iz sinx<x za x iz [0, pipola]). Stoga je na domeni [latex] [3/pi, + \infty> [/latex] funkcija padajuća. I to je to.
3.15 d)
Ovaj kosinus u brojniku poprima samo konačno mnogo vijednosti: i to samo -1, 1 i 0. Kada si raspišemo prvih par članova dobijemo:
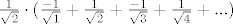
Ovaj red unutar zagrada po leibnitzu konvergira, ali po integralnom apsolutno ne konvergira.
A grupa:
Primijetimo da je 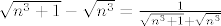 , što teži u nulu kad n ide u beskonačnost. , što teži u nulu kad n ide u beskonačnost.
Zato po usporednom kriteriju (smijemo ga lupati jer su sigurno svi članovi pozitivni), početni red konvergira ako i samo ako konvergira red kojemu su članovi 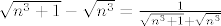 , a to opet po usporednom kriteriju konvergira ako i samo ako konvergira red kojemu su članovi , a to opet po usporednom kriteriju konvergira ako i samo ako konvergira red kojemu su članovi 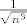 . Ovaj zadnji red znamo da konvergira, integralni kriterij (eksponent mu je 1.5). . Ovaj zadnji red znamo da konvergira, integralni kriterij (eksponent mu je 1.5).
B grupa (a slično ide u i D):
Da bi dokazali konvergenciju, lupit ćemo leibnitzov kriterij, no zato trebamo pokazati da su svi izrazi 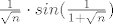 pozitivni i da su padajući. Očito su pozitivni (jer su argumenti sinusa u intervalu 0 do pipola). Padajućost ćemo dokazati deriviranjem: definiramo si funkciju pozitivni i da su padajući. Očito su pozitivni (jer su argumenti sinusa u intervalu 0 do pipola). Padajućost ćemo dokazati deriviranjem: definiramo si funkciju 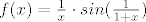 . Njena derivacija je negativna, pa je funkcija padajuća, pa je i niz padajuć. Joj, da, trebamo pokazati i da niz teži u nulu, no to je također očito. . Njena derivacija je negativna, pa je funkcija padajuća, pa je i niz padajuć. Joj, da, trebamo pokazati i da niz teži u nulu, no to je također očito.
D: grupa:
Opet si definiramo funkciju, 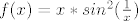 . Njena derivacija je . Njena derivacija je 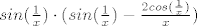 . Za nju nije tako očito da je manja od nule, pa ću malo više argumentirati. Naime, za . Za nju nije tako očito da je manja od nule, pa ću malo više argumentirati. Naime, za 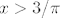 vrijedi da je vrijedi da je 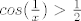 , pa je za takve ikseve , pa je za takve ikseve 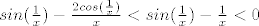 (zadnja nejednakost slijedi iz sinx<x za x iz [0, pipola]). Stoga je na domeni (zadnja nejednakost slijedi iz sinx<x za x iz [0, pipola]). Stoga je na domeni 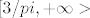 funkcija padajuća. I to je to. funkcija padajuća. I to je to.
|




