| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
rat in a cage
Forumaš(ica)


Pridružen/a: 25. 11. 2004. (21:45:48)
Postovi: (22C)16
Lokacija: Zg
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 15:18 pet, 17. 4. 2009 Naslov: Postano: 15:18 pet, 17. 4. 2009 Naslov: |
    |
|
|
C je poliedarski skup, dakle [latex]C = \{x \in \mathbb{R}^n \colon Ax \leq b} \}[/latex] za neki [latex]b[/latex].
Pretpostavimo da je [latex]b_i < 0[/latex], za neki [latex]i[/latex]. Tada [latex]0 \notin C[/latex], ali C je konus pa je to nemoguce.
Pretpostavimo sad da [latex]b_i > 0[/latex] i [latex]\exists x \in C[/latex] t.d. [latex]a^i x = M > 0[/latex] (ako takav ne postoji, onda za komponentu [latex]b_i[/latex] mozemo odabrati vrijednost 0).
No, kako je C konus, tada [latex](\forall t \geq 0)tx \in C[/latex]. No onda uzmemo [latex]t = 2 \frac{b_i}{M}[/latex], pa je [latex]a^i tx = 2 \frac{b_i}{M} M = 2 b_i[/latex], pa slijedi da [latex]tx \notin C[/latex] sto je kontradikcija.
Dakle vrijedi [latex]C = \{x \in \mathbb{R}^n \colon Ax \leq 0} \}[/latex].
C je poliedarski skup, dakle 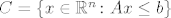 za neki za neki 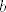 . .
Pretpostavimo da je 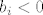 , za neki , za neki  . Tada . Tada 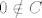 , ali C je konus pa je to nemoguce. , ali C je konus pa je to nemoguce.
Pretpostavimo sad da 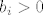 i i  t.d. t.d. 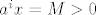 (ako takav ne postoji, onda za komponentu (ako takav ne postoji, onda za komponentu 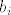 mozemo odabrati vrijednost 0). mozemo odabrati vrijednost 0).
No, kako je C konus, tada 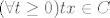 . No onda uzmemo . No onda uzmemo 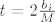 , pa je , pa je 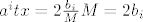 , pa slijedi da , pa slijedi da 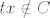 sto je kontradikcija. sto je kontradikcija.
Dakle vrijedi 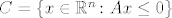 . .
_________________
Bri
|
|
| [Vrh] |
|
rat in a cage
Forumaš(ica)


Pridružen/a: 25. 11. 2004. (21:45:48)
Postovi: (22C)16
Lokacija: Zg
|
|
| [Vrh] |
|
anatomik
Forumaš(ica)
Pridružen/a: 03. 05. 2012. (10:32:11)
Postovi: (20)16
|
|
| [Vrh] |
|
|





