| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 19:38 pet, 9. 12. 2005 Naslov: Zadaci vezani uz infimum i supremum Postano: 19:38 pet, 9. 12. 2005 Naslov: Zadaci vezani uz infimum i supremum |
    |
|
|
Na stranicama Metematičke Analize 1&2, pd linkom "dodatni materijali" možete naći zadatke vezane uz gradivo infimuma i supremuma. Ili jednostavnije, skinete ih s:
http://web.math.hr/nastava/analiza/files/infsup.pdf
To je [b]neobavezno[/b], tj. nije zadaca, vec zadaci za vjezbu.
Neki zadaci jesu tezi, no predstavljaju dobru vjezbu pred 3. zadacu, odnosno "daleki" 2. kolokvij.
Nadam se da ce se naci odaziva. :)
Također, mada sad baš i nije aktualno, na istoj stranici možete naći zadatke vezane uz kvadratnu funkciju, pa ak je nekom dosadno... :D
Na stranicama Metematičke Analize 1&2, pd linkom "dodatni materijali" možete naći zadatke vezane uz gradivo infimuma i supremuma. Ili jednostavnije, skinete ih s:
http://web.math.hr/nastava/analiza/files/infsup.pdf
To je neobavezno, tj. nije zadaca, vec zadaci za vjezbu.
Neki zadaci jesu tezi, no predstavljaju dobru vjezbu pred 3. zadacu, odnosno "daleki" 2. kolokvij.
Nadam se da ce se naci odaziva. 
Također, mada sad baš i nije aktualno, na istoj stranici možete naći zadatke vezane uz kvadratnu funkciju, pa ak je nekom dosadno... 
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 20:58 pet, 9. 12. 2005 Naslov: Postano: 20:58 pet, 9. 12. 2005 Naslov: |
    |
|
|
[quote="mladac"]jel postoje negdje i rješenja?[/quote]
Ideja tih zadataka nije da vam ih damo rjesene, nego da sami probate rješiti, pa ako ne ide, tj. ako negdje zapnete onda pitate, tako se najbolje nauci 8)
| mladac (napisa): | | jel postoje negdje i rješenja? |
Ideja tih zadataka nije da vam ih damo rjesene, nego da sami probate rješiti, pa ako ne ide, tj. ako negdje zapnete onda pitate, tako se najbolje nauci 
Zadnja promjena: Ilja; 21:10 pet, 9. 12. 2005; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
fireball
Forumaš(ica)


Pridružen/a: 07. 10. 2005. (18:49:17)
Postovi: (4AB)16
Spol: 
Lokacija: s rukom u vatri i nogom u grobu
|
|
| [Vrh] |
|
mladac
Forumaš(ica)


Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol: 
Lokacija: zg
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
fireball
Forumaš(ica)


Pridružen/a: 07. 10. 2005. (18:49:17)
Postovi: (4AB)16
Spol: 
Lokacija: s rukom u vatri i nogom u grobu
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 1:26 ned, 11. 12. 2005 Naslov: rješenja zadataka Postano: 1:26 ned, 11. 12. 2005 Naslov: rješenja zadataka |
    |
|
|
Evo provjerio i mislim da ne bi trebalo biti grešaka. Rješenja zadataka su redom:
[b]1. zad[/b]
inf S = -1/4
sup S = 12
[b]2. zad[/b]
inf S = 1/2
sup S = 11/6
[b]3. zad[/b]
S nije omeđen odozdo
sup S = 1
[b]4. zad[/b]
inf S = 0
sup S = 1
[b]5. zad[/b]
inf S = 1/4
sup S = 3
[b]6. zad[/b]
inf S = 1
S nije omeđen odozgo
[b]7. zad[/b]
inf S = -6
sup S = 6
Sretno!
P.S. također zahvalite i našem vjekovcu, koji čim je spazio zadatke naprosto nije mogao odoliti, a da ih odmah prije svih vas ne riješi i začudo, dečec je dobro rješio, [b]bravo vjekovac[/b], no moraš malo i čorit, a ne tu samo računat :wink:
Evo provjerio i mislim da ne bi trebalo biti grešaka. Rješenja zadataka su redom:
1. zad
inf S = -1/4
sup S = 12
2. zad
inf S = 1/2
sup S = 11/6
3. zad
S nije omeđen odozdo
sup S = 1
4. zad
inf S = 0
sup S = 1
5. zad
inf S = 1/4
sup S = 3
6. zad
inf S = 1
S nije omeđen odozgo
7. zad
inf S = -6
sup S = 6
Sretno!
P.S. također zahvalite i našem vjekovcu, koji čim je spazio zadatke naprosto nije mogao odoliti, a da ih odmah prije svih vas ne riješi i začudo, dečec je dobro rješio, bravo vjekovac, no moraš malo i čorit, a ne tu samo računat 
|
|
| [Vrh] |
|
fireball
Forumaš(ica)


Pridružen/a: 07. 10. 2005. (18:49:17)
Postovi: (4AB)16
Spol: 
Lokacija: s rukom u vatri i nogom u grobu
|
|
| [Vrh] |
|
aska
Forumaš(ica)
Pridružen/a: 02. 11. 2005. (20:01:50)
Postovi: (5B)16
|
 Postano: 12:06 ned, 11. 12. 2005 Naslov: Postano: 12:06 ned, 11. 12. 2005 Naslov: |
    |
|
|
Oke,ja imam jedno vezano za prvi zadatak. Nisam sigurna jel dobro radim..
Daklem,svedem to na uniju dva slucaja : q^2-3q+2 i q^2+3q+2. q je iz Q+,iz intervala (0,2].
Iz grafova vidim sta su sup i inf,i cak uspijem dokazat da je -1/4 inf za prvi slucaj.
Al sad nisam sigurna jel ovo dalje dobro. Mislila sam svaki slucaj rastavit na uniju dva slucaja,kad je fja rastuca i kad je padajuca (to isto moram dokazat?). I onda to dokazujem implikacijama koje vrijede za rastucu/padajucu fju? (A onda ide propozicija za sup/inf unije skupova)
Dobijem dobar rezultat al nisam sigurna a)jel to dobar postupak;zapravo jel se to opcenito radi tako s kvadratnim funkcijama i b)jel postoji nesto jednostavnije?
:thankyou:
Oke,ja imam jedno vezano za prvi zadatak. Nisam sigurna jel dobro radim..
Daklem,svedem to na uniju dva slucaja : q^2-3q+2 i q^2+3q+2. q je iz Q+,iz intervala (0,2].
Iz grafova vidim sta su sup i inf,i cak uspijem dokazat da je -1/4 inf za prvi slucaj.
Al sad nisam sigurna jel ovo dalje dobro. Mislila sam svaki slucaj rastavit na uniju dva slucaja,kad je fja rastuca i kad je padajuca (to isto moram dokazat?). I onda to dokazujem implikacijama koje vrijede za rastucu/padajucu fju? (A onda ide propozicija za sup/inf unije skupova)
Dobijem dobar rezultat al nisam sigurna a)jel to dobar postupak;zapravo jel se to opcenito radi tako s kvadratnim funkcijama i b)jel postoji nesto jednostavnije?

_________________  |
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
 Postano: 13:44 ned, 11. 12. 2005 Naslov: Postano: 13:44 ned, 11. 12. 2005 Naslov: |
    |
|
|
[quote="aska"]Oke,ja imam jedno vezano za prvi zadatak. Nisam sigurna jel dobro radim..
Daklem,svedem to na uniju dva slucaja : q^2-3q+2 i q^2+3q+2. q je iz Q+,iz intervala (0,2].
Iz grafova vidim sta su sup i inf,i cak uspijem dokazat da je -1/4 inf za prvi slucaj.
Al sad nisam sigurna jel ovo dalje dobro. Mislila sam svaki slucaj rastavit na uniju dva slucaja,kad je fja rastuca i kad je padajuca (to isto moram dokazat?). I onda to dokazujem implikacijama koje vrijede za rastucu/padajucu fju? (A onda ide propozicija za sup/inf unije skupova)
Dobijem dobar rezultat al nisam sigurna a)jel to dobar postupak;zapravo jel se to opcenito radi tako s kvadratnim funkcijama i b)jel postoji nesto jednostavnije?
:thankyou:[/quote]
To je to, znači [latex]S[/latex] prikažeš kao uniju dva podskupa [latex]S_1[/latex] i [latex] S_2[/latex], ovisno o kosinunsu. Znači [latex]\cos(mn\pi)=1[/latex] točno onda kada je barem jedan od [latex]m,n[/latex] paran i budući se svaki pozitivni racionalni broj [latex]q=\frac{m}{n} \in \mathbb{Q}_+[/latex] može prikazati kao kvocijent dva parna prirodna broja
([latex]q=\frac{m}{n}=\frac{2m}{2n}[/latex]), to je prvi skup
zapravo [latex]S_1= f(\langle 0, 2] \cap \mathbb{Q})[/latex], gdje je [latex]f(x):=x^2+3x+2[/latex]. Kako je [latex]f[/latex] strogo rastuća na [latex][-\frac{3}{2}, +\infty \rangle[/latex] to je i restrikcija od [latex]f[/latex]
na [latex]\langle 0, 2] \cap \mathbb{Q}[/latex] strogo rastuća, pa je [latex]\sup S_1 = \max S_1 =f(2)=12[/latex] (bitna primjedba je to što je ovdje([latex] 2 \in \langle 0, 2] \cap \mathbb{Q}[/latex]).
Vjerojatno si i ti tako išla, no napisao sam za svaki slučaj jer drugi podskup ipak nije "tako lijep", jer je oblika
[latex]S_2=\bigg\{ \bigg(\frac{2n-1}{2m-1}\bigg)^2 -3\frac{2n-1}{2m-1} +2 : \ m,n \in \mathbb{N}, \frac{2n-1}{2m-1} \leq 2\bigg\}[/latex]. Ako definiraš funkciju [latex]g(x):=x^2-3x+2[/latex], tada je, slično kao i u prvom slučaju [latex]S_2=g(S'_2)[/latex], gdje je [latex]S'_2:=\{\frac{2n-1}{2m-1}: \ m,n \in \mathbb{N}, \frac{2n-1}{2m-1} \leq 2\}[/latex] pa je [latex]S_2[/latex] omeđen odozdo s [latex]-\frac{1}{4}=g(\frac{3}{2})[/latex]. No tu je problem što [latex]-\frac{1}{4}[/latex] nije element od [latex]S_2[/latex] (jer [latex]\frac{3}{2}[/latex] nije element od [latex]S'_2[/latex]), no koristeći Arhimedov aksiom, možeš dokazati da je [latex]\inf S_2 =-\frac{1}{4}[/latex], samo trebaš elemente iz [latex]S_2[/latex] prikazati u "pogodnijoj formi". (uputa: [latex]g(x)=(x-\frac{3}{2})^2 - \frac{1}{4}[/latex])
Na kraju treba još primijetiti da ne treba uopće tražiti [latex]\sup S_2[/latex] i [latex]\inf S_1[/latex] jer je u svakom slučaju [latex]\sup S_1 \geq \sup S_2[/latex] i [latex]\inf S_1 \geq \inf S_2[/latex].
Znači, prema onoj propoziciji s vježbi je
[latex]\sup S = \max \{ \sup S_1, \sup S_2 \}= \sup S_1 = 12
= \max S[/latex] i
[latex]\inf S = \min \{ \inf S_1, \inf S_2 \}= \inf S_2 = - \frac{1}{4}[/latex].
| aska (napisa): | Oke,ja imam jedno vezano za prvi zadatak. Nisam sigurna jel dobro radim..
Daklem,svedem to na uniju dva slucaja : q^2-3q+2 i q^2+3q+2. q je iz Q+,iz intervala (0,2].
Iz grafova vidim sta su sup i inf,i cak uspijem dokazat da je -1/4 inf za prvi slucaj.
Al sad nisam sigurna jel ovo dalje dobro. Mislila sam svaki slucaj rastavit na uniju dva slucaja,kad je fja rastuca i kad je padajuca (to isto moram dokazat?). I onda to dokazujem implikacijama koje vrijede za rastucu/padajucu fju? (A onda ide propozicija za sup/inf unije skupova)
Dobijem dobar rezultat al nisam sigurna a)jel to dobar postupak;zapravo jel se to opcenito radi tako s kvadratnim funkcijama i b)jel postoji nesto jednostavnije?
 |
To je to, znači  prikažeš kao uniju dva podskupa prikažeš kao uniju dva podskupa 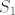 i i 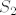 , ovisno o kosinunsu. Znači , ovisno o kosinunsu. Znači 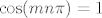 točno onda kada je barem jedan od točno onda kada je barem jedan od 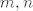 paran i budući se svaki pozitivni racionalni broj paran i budući se svaki pozitivni racionalni broj 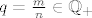 može prikazati kao kvocijent dva parna prirodna broja može prikazati kao kvocijent dva parna prirodna broja
(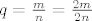 ), to je prvi skup ), to je prvi skup
zapravo 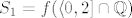 , gdje je , gdje je 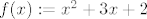 . Kako je . Kako je  strogo rastuća na strogo rastuća na 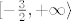 to je i restrikcija od to je i restrikcija od 
na 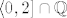 strogo rastuća, pa je strogo rastuća, pa je 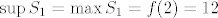 (bitna primjedba je to što je ovdje( (bitna primjedba je to što je ovdje(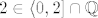 ). ).
Vjerojatno si i ti tako išla, no napisao sam za svaki slučaj jer drugi podskup ipak nije "tako lijep", jer je oblika
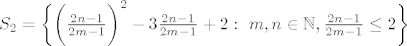 . Ako definiraš funkciju . Ako definiraš funkciju 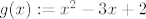 , tada je, slično kao i u prvom slučaju , tada je, slično kao i u prvom slučaju 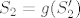 , gdje je , gdje je 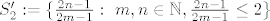 pa je pa je 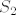 omeđen odozdo s omeđen odozdo s 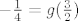 . No tu je problem što . No tu je problem što 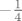 nije element od nije element od 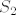 (jer (jer 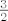 nije element od nije element od 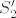 ), no koristeći Arhimedov aksiom, možeš dokazati da je ), no koristeći Arhimedov aksiom, možeš dokazati da je 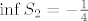 , samo trebaš elemente iz , samo trebaš elemente iz 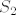 prikazati u "pogodnijoj formi". (uputa: prikazati u "pogodnijoj formi". (uputa: 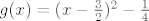 ) )
Na kraju treba još primijetiti da ne treba uopće tražiti 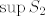 i i 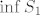 jer je u svakom slučaju jer je u svakom slučaju 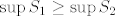 i i 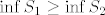 . .
Znači, prema onoj propoziciji s vježbi je
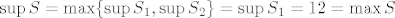 i i
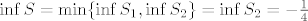 . .
Zadnja promjena: Ilja; 23:49 ned, 11. 12. 2005; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
aska
Forumaš(ica)
Pridružen/a: 02. 11. 2005. (20:01:50)
Postovi: (5B)16
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
Gost
|
 Postano: 21:20 uto, 3. 1. 2006 Naslov: Postano: 21:20 uto, 3. 1. 2006 Naslov: |
    |
|
|
vezano uz prvi zadatak 3. zadace i opcenito:zasto smo na vjezbama prvo pisali:infS=min(infs1,infs2) a kasnije je to bilo min(infs1infs2,sups1sups2,...)? I ako S rasatvimo na umnožak 3 skupa je li onda njegov infS=min(infs1infs2infs3,sups1sups2sups3,infs1infs2sups3,....)?
vezano uz prvi zadatak 3. zadace i opcenito:zasto smo na vjezbama prvo pisali:infS=min(infs1,infs2) a kasnije je to bilo min(infs1infs2,sups1sups2,...)? I ako S rasatvimo na umnožak 3 skupa je li onda njegov infS=min(infs1infs2infs3,sups1sups2sups3,infs1infs2sups3,....)?
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 22:11 uto, 3. 1. 2006 Naslov: Postano: 22:11 uto, 3. 1. 2006 Naslov: |
    |
|
|
[quote="Anonymous"]vezano uz prvi zadatak 3. zadace i opcenito:zasto smo na vjezbama prvo pisali:infS=min(infs1,infs2) a kasnije je to bilo min(infs1infs2,sups1sups2,...)? I ako S rasatvimo na umnožak 3 skupa je li onda njegov infS=min(infs1infs2infs3,sups1sups2sups3,infs1infs2sups3,....)?[/quote]
opcenito ti je super u tim zadacima to kaj nemas puno mogucnosti jer su obicno samo dva skupa, pa pogledas sve kombinacije umnozaka i odaberes najmanji i najveci i to je to...
isto radis ak imas 3 skupa sam kaj onda ima mrvicu vise kombinacija :D
a ne kuzim tocno kaj pitas ovo sa vjezbi... :grebgreb:
| Anonymous (napisa): | | vezano uz prvi zadatak 3. zadace i opcenito:zasto smo na vjezbama prvo pisali:infS=min(infs1,infs2) a kasnije je to bilo min(infs1infs2,sups1sups2,...)? I ako S rasatvimo na umnožak 3 skupa je li onda njegov infS=min(infs1infs2infs3,sups1sups2sups3,infs1infs2sups3,....)? |
opcenito ti je super u tim zadacima to kaj nemas puno mogucnosti jer su obicno samo dva skupa, pa pogledas sve kombinacije umnozaka i odaberes najmanji i najveci i to je to...
isto radis ak imas 3 skupa sam kaj onda ima mrvicu vise kombinacija 
a ne kuzim tocno kaj pitas ovo sa vjezbi... 
|
|
| [Vrh] |
|
ivanam
Forumaš s poteškoćama u pisanju

Pridružen/a: 21. 12. 2005. (16:25:02)
Postovi: (14)16
|
 Postano: 0:26 sri, 4. 1. 2006 Naslov: Postano: 0:26 sri, 4. 1. 2006 Naslov: |
    |
|
|
[quote="Ignavia"][quote="Anonymous"]vezano uz prvi zadatak 3. zadace i opcenito:zasto smo na vjezbama prvo pisali:infS=min(infs1,infs2) a kasnije je to bilo min(infs1infs2,sups1sups2,...)? I[/quote]
a ne kuzim tocno kaj pitas ovo sa vjezbi... :grebgreb:[/quote]
ja nisam bila taj dan na vježbama, ali mi intucija govori da je to možda zato što je prva tvrdnje iskazana kada su S1 i S2 podskupovi od R+, a onda je napisana kuharica kak se postupa u općem slučaju (ako vam se ne da misliti) i to točno onako kako je drugarica Ignavia rekla. :D
| Ignavia (napisa): | | Anonymous (napisa): | | vezano uz prvi zadatak 3. zadace i opcenito:zasto smo na vjezbama prvo pisali:infS=min(infs1,infs2) a kasnije je to bilo min(infs1infs2,sups1sups2,...)? I |
a ne kuzim tocno kaj pitas ovo sa vjezbi...  |
ja nisam bila taj dan na vježbama, ali mi intucija govori da je to možda zato što je prva tvrdnje iskazana kada su S1 i S2 podskupovi od R+, a onda je napisana kuharica kak se postupa u općem slučaju (ako vam se ne da misliti) i to točno onako kako je drugarica Ignavia rekla. 
|
|
| [Vrh] |
|
Drvena Matrija
Forumaš s poteškoćama u pisanju


Pridružen/a: 21. 12. 2005. (00:11:50)
Postovi: (11)16
Lokacija: u trajnoj odsutnosti (dok me ne zbrišu)
|
|
| [Vrh] |
|
ivanam
Forumaš s poteškoćama u pisanju


Pridružen/a: 21. 12. 2005. (16:25:02)
Postovi: (14)16
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)


Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
|
| [Vrh] |
|
mare
Gost
|
 Postano: 14:35 čet, 5. 1. 2006 Naslov: Postano: 14:35 čet, 5. 1. 2006 Naslov: |
    |
|
|
Helou,dragi matematičari, molila bih da se nađe neka dobra duša da mi pomogne riješiti 3. zadatak sa infimumima i supremumima šta je Mr. Ilja stavija na net. Mislim, jasno mi je da je supremum 1 zato što je cijeli ovaj razlomak sigurno veći od 0, i isto tako da skup nije ograničen odozdo jer kad npr. pustin n da ide u beskonačnost tada i cijeli skup ode u beskonačnost...sad mi se u svemu tome čini da sam to malo onako zdravo seljački riješila, tj. ne znam dokazat :cry:
pliz helpajte
:thankyou:
Helou,dragi matematičari, molila bih da se nađe neka dobra duša da mi pomogne riješiti 3. zadatak sa infimumima i supremumima šta je Mr. Ilja stavija na net. Mislim, jasno mi je da je supremum 1 zato što je cijeli ovaj razlomak sigurno veći od 0, i isto tako da skup nije ograničen odozdo jer kad npr. pustin n da ide u beskonačnost tada i cijeli skup ode u beskonačnost...sad mi se u svemu tome čini da sam to malo onako zdravo seljački riješila, tj. ne znam dokazat 
pliz helpajte

|
|
| [Vrh] |
|
|











