zadatak s kolokvija 2002.

[Gost]

Zadatak:
Neka je A iz M_2(R), A=A^t (transponirano). Neka je detA>0 i a_22<0. Dokažite da su tada obje svojstvene vrijednosti <0.

E sad, ja krenem ovak:
det A=x_1*x_2 (x_1 i x_2 su svojstvene vrijednosti)
Da bi detA>0 mora i a_11 biti <0 (raspišem detA pa se to lako vidi)
kako je detA>0 onda mora biti x_1 i x_2 oba >0 ili oba <0
kak se sad dokaže da su oba manji od 0?
Please help, sutra je kolokvij!

[ahri]

oke, dakle ovako si isao:
matrica je simetricna pa je a_12=a_21 = b

det(A)= a_11*a_22 - b^2 >0
slijedi a_11 <0, jer a_22 <0, a lijevi umnozak je veci od desnog, koji je uvijek pozitivan.

racunamo svojstvene vrijednosti (k1 i k2 ce biti svojstvene vrijednosti):
det(A-kI) = 0
I je naravno identiteta.

(a_11 - k)(a_22-k) - b^2 = 0

k^2 - k(a_11 + a_22) + a_11*a_22 - b^2 = 0

znamo da je a_11 + a_22 sigurno manji od nule, jer su oba manja od nule. oznacimo to sa -B radi lakseg uvidjanja rjesenja.

k^2 + Bk + det(A) = 0

dakle, B je pozitivan, det(A) je pozitivna, k^2 je pozitivan.

dakle, jedino kada ova jednakost moze biti jednaka nuli je kada su svi nula (a nisu) ili kada je k<0.

dakle, svojstvene vrijednosti su manje od nule :)

_________________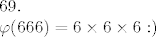