Preminuo je prof. Singer (informacija)

[vsego]

Sinoć je preminuo prof. Saša Singer.



Bio je jedan od pionira numeričke matematike u Hrvatskoj, poznat i cijenjen među najboljim svjetskim grupama. Nastavno, studenti ga desetljećima znaju kao vrhunskog i zabavnog predavača, te oštrog i pravednog ispitivača. Većini nas je nezamislivo završiti fax, a ne proći Singera barem na Programiranjima i Numeričkoj matematici.

Osobno, imao sam čast raditi sa Sašom nekoliko godina, u nastavi i na doktoratu, i ta iskustva su mi među najdražim uspomenama koje imam. Bio mi je formalno nadređeni nastavnik i mentor na doktoratu, no zapravo izuzetan prijatelj od kojeg sam mnogo naučio, kako profesionalno tako i osobno.

Detalje ispraćaja ću objaviti kad ih saznam.

[Melkor]

Tragičan gubitak.

Saša mi je predavao Složenost algoritama i Aritmetičke i algebarske algoritme, te mi je bio u komisiji za diplomski ispit. Kad sam se prijavljivao na doktorske studije, pomogao mi je napisavši pismo preporuke.

Sa Složenosti se i nakon 13 godina još dobro sjećam analize Kruskalovog algoritma za minimalno razapinjuće stablo u kojem ključnu ulogu igra union-find struktura podataka. U optimalnoj izvedbi, operacije union i find nad elemenata imaju amortiziranu složenost 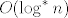, pri čemu je 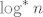iterirani logaritam. Sjećam se kako je Saša entuzijastično objašnjavao da iterirani logaritam nevjerojatno sporo raste – za sve praktične potrebe je konstantan. Otada ne mogu pomisliti na Kruskalov algoritam i union-find strukturu, a da se ne sjetim i Saše.

_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.

[vsego]

Posljednji ispraćaj prof. Singera bit će u srijedu, 23.9., u 13:20 na Mirogoju.

_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.