|
[quote="fizičar_u_problemima"]Ovaj post sam postao na raspravama na fizici, ali kako stvari stoje fizičari se baš ne trgaju da odgovore, pa se nadam da su vas tu nešto više naučili nego nas tamo. :lol: [/quote]
Mi ti ovdje zapravo ništa ne znamo, evo ja ću ti odgovoriti po prilici. :lol:
[quote="fizičar_u_problemima"]Moze li netko pojasniti vezu između Lagrangeovog teorema i Taylorovog teorema srednje vrijednosti (mozda sa primjerom neke funkcije)? [/quote]
[b]Taylorov teorem:[/b]
Pretpostavimo da je f:[a,b]->R klase C^n na [a,b] i ima (n+1)-vu derivaciju na <a,b>. Tada za svake [latex]x,x_0[/latex] iz I postoji [latex]c_x[/latex] između [latex]x_0[/latex] i [latex]x[/latex] takav da vrijedi
[latex]f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+\ldots+\\
+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n+
\frac{f^{(n+1)}(c_x)}{(n+1)!}(x-x_0)^{n+1}[/latex].
[b]Lagrangeov teorem[/b] je specijalni slučaj Taylorovog za n=0:
Pretpostavimo da je f:[a,b]->R neprekidna (=klase C^0) na [a,b] i ima derivaciju na <a,b>. Tada za svake [latex]x,x_0[/latex] iz I postoji [latex]c_x[/latex] između [latex]x_0[/latex] i [latex]x[/latex] takav da vrijedi
[latex]f(x)=f(x_0)+f'(c_x)(x-x_0)[/latex].
Prividna razlika je što se kod formulacije Lagrangeovog teorema često uzima specijalno x_0=a, x=b, ali to ne smanjuje općenitost (naprosto gledamo segment [latex][x_0,x][/latex] ili [latex][x,x_0][/latex] umjesto [a,b]). U toj formulaciji formulu onda pišemo:
[latex]f(b)=f(a)+f'(c_x)(b-a)[/latex]
ili možda ljepše
[latex]f'(c_x)=\frac{f(b)-f(a)}{b-a}[/latex].
[quote="fizičar_u_problemima"]A i uopce mi nije jasno sto predstavlja onaj [latex]c_x[/latex] i sto treba znaciti to sto se on nalazi između [latex]x_0[/latex] i [latex]x[/latex].[/quote]
To znači:
ako je [latex]x_0<x[/latex], onda je [latex]x_0<c_x<x[/latex],
ako je [latex]x<x_0[/latex], onda je [latex]x<c_x<x_0[/latex].
Ako je pak [latex]x=x_0[/latex], onda je sasvim svejedno koji [latex]c_x[/latex] uzmemo, npr. [latex]c_x=x_0=x[/latex].
[quote="fizičar_u_problemima"]Kako bismo si mogli taj ostatak prilikom razvoja funkcije u red vizualizirati? u smislu mozemo li mozda taj ostatak prikazati grafom pa onda iz slike vidjeti 'koliko nam fali do prave funkcije'?[/quote]
Za n=1 skiciraj si graf od f i tangentu na njega u točki [latex](x_0,f(x_0))[/latex], to je graf afine funkcije [latex]T_1(x)=f(x_0)+f'(x_0)(x-x_0)[/latex]. Razlika [latex]f(x)-T_1(x)[/latex] je ostatak Taylorovog reda.
Za n=2, pokušaj si (umjesto pravca) zamisliti parabolu koja najbolje priliježe uz graf od f u točki [latex](x_0,f(x_0))[/latex], a ostatak reda je tada razlika f(x) i pripadne kvadratne funkcije [latex]T_2(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{1}{2}f''(x_0)(x-x_0)^2[/latex].
Itd.
[quote="fizičar_u_problemima"]Hoću reći je li to baš neka zasebna funkcija koju trebamo zbrojiti sa Taylorovim polinomom da bismo dobili originalnu f(x)? [/quote]
To je upravo definicija "ostatka" Taylorovog reda: ono s čime moraš zbrojiti Taylorov polinom da dobiješ polaznu funkciju. (Naravno, pretpostavljamo da se polazna funkcija uopće može razviti u Taylorov red.)
[quote="fizičar_u_problemima"]Ako jest, zašto je bitno da je (n+1)-va derivacija baš u toj nekoj Cx koja je između C i X?[/quote]
Pa nije baš uvijek jako bitno, nego je korisno za ocjenjivanje. Npr. ako ništa drugo, barem znamo da kada je [latex]x[/latex] blizu [latex]x_0[/latex], onda ostatak [latex]\frac{f^{(n+1)}(c_x)}{(n+1)!}(x-x_0)^{n+1}[/latex]
ovisi o ponašanju funkcije (zapravo njene (n+1)-ve derivacije) blizu [latex]x_0[/latex] (jer je [latex]c_x[/latex] između [latex]x_0[/latex] i [latex]x[/latex] pa je isto "blizu" [latex]x_0[/latex]).
[quote="fizičar_u_problemima"]I kakve veze ima dakle taj Taylorov tm srednje vrijednosti s time da "paralelno sa sekantom koja prolazi nekim tockama (a,f(a)) i (b,f(b)) postoji tangenta s diralistem (c,f(c)) na grafu iste te funkcije paralelna sa onom sekantom" sto bi trebao biti Lagrangeov teorem."[/quote]
To je geometrijska interpretacija Lagrangeovog teorema. Taylorov teorem nema takvu lijepu geometrijsku interpretaciju.
| fizičar_u_problemima (napisa): | Ovaj post sam postao na raspravama na fizici, ali kako stvari stoje fizičari se baš ne trgaju da odgovore, pa se nadam da su vas tu nešto više naučili nego nas tamo.  |
Mi ti ovdje zapravo ništa ne znamo, evo ja ću ti odgovoriti po prilici. 
| fizičar_u_problemima (napisa): | | Moze li netko pojasniti vezu između Lagrangeovog teorema i Taylorovog teorema srednje vrijednosti (mozda sa primjerom neke funkcije)? |
Taylorov teorem:
Pretpostavimo da je f:[a,b]→R klase C^n na [a,b] i ima (n+1)-vu derivaciju na <a,b>. Tada za svake 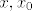 iz I postoji iz I postoji 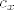 između između  i i  takav da vrijedi takav da vrijedi
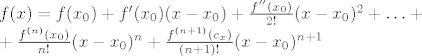 . .
Lagrangeov teorem je specijalni slučaj Taylorovog za n=0:
Pretpostavimo da je f:[a,b]→R neprekidna (=klase C^0) na [a,b] i ima derivaciju na <a,b>. Tada za svake 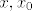 iz I postoji iz I postoji 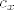 između između  i i  takav da vrijedi takav da vrijedi
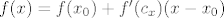 . .
Prividna razlika je što se kod formulacije Lagrangeovog teorema često uzima specijalno x_0=a, x=b, ali to ne smanjuje općenitost (naprosto gledamo segment 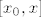 ili ili 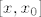 umjesto [a,b]). U toj formulaciji formulu onda pišemo: umjesto [a,b]). U toj formulaciji formulu onda pišemo:

ili možda ljepše
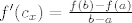 . .
| fizičar_u_problemima (napisa): | A i uopce mi nije jasno sto predstavlja onaj 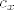 i sto treba znaciti to sto se on nalazi između i sto treba znaciti to sto se on nalazi između  i i  . . |
To znači:
ako je 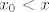 , onda je , onda je 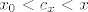 , ,
ako je 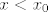 , onda je , onda je 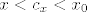 . .
Ako je pak 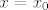 , onda je sasvim svejedno koji , onda je sasvim svejedno koji 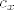 uzmemo, npr. uzmemo, npr. 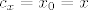 . .
| fizičar_u_problemima (napisa): | | Kako bismo si mogli taj ostatak prilikom razvoja funkcije u red vizualizirati? u smislu mozemo li mozda taj ostatak prikazati grafom pa onda iz slike vidjeti 'koliko nam fali do prave funkcije'? |
Za n=1 skiciraj si graf od f i tangentu na njega u točki 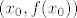 , to je graf afine funkcije , to je graf afine funkcije  . Razlika . Razlika 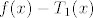 je ostatak Taylorovog reda. je ostatak Taylorovog reda.
Za n=2, pokušaj si (umjesto pravca) zamisliti parabolu koja najbolje priliježe uz graf od f u točki 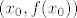 , a ostatak reda je tada razlika f(x) i pripadne kvadratne funkcije , a ostatak reda je tada razlika f(x) i pripadne kvadratne funkcije 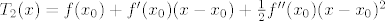 . .
Itd.
| fizičar_u_problemima (napisa): | | Hoću reći je li to baš neka zasebna funkcija koju trebamo zbrojiti sa Taylorovim polinomom da bismo dobili originalnu f(x)? |
To je upravo definicija "ostatka" Taylorovog reda: ono s čime moraš zbrojiti Taylorov polinom da dobiješ polaznu funkciju. (Naravno, pretpostavljamo da se polazna funkcija uopće može razviti u Taylorov red.)
| fizičar_u_problemima (napisa): | | Ako jest, zašto je bitno da je (n+1)-va derivacija baš u toj nekoj Cx koja je između C i X? |
Pa nije baš uvijek jako bitno, nego je korisno za ocjenjivanje. Npr. ako ništa drugo, barem znamo da kada je  blizu blizu  , onda ostatak , onda ostatak 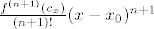
ovisi o ponašanju funkcije (zapravo njene (n+1)-ve derivacije) blizu  (jer je (jer je 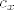 između između  i i  pa je isto "blizu" pa je isto "blizu"  ). ).
| fizičar_u_problemima (napisa): | | I kakve veze ima dakle taj Taylorov tm srednje vrijednosti s time da "paralelno sa sekantom koja prolazi nekim tockama (a,f(a)) i (b,f(b)) postoji tangenta s diralistem (c,f(c)) na grafu iste te funkcije paralelna sa onom sekantom" sto bi trebao biti Lagrangeov teorem." |
To je geometrijska interpretacija Lagrangeovog teorema. Taylorov teorem nema takvu lijepu geometrijsku interpretaciju.
|






