| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 11:38 čet, 19. 8. 2004 Naslov: Integrali-teorem Postano: 11:38 čet, 19. 8. 2004 Naslov: Integrali-teorem |
    |
|
|
[color=green]Teorem kaže:
f:[a,b] -> IR neprekidna => f uniformno(jednoliko) neprekidna[/color]
Dokaz:
[color=darkblue]Pretpostavimo suprotno,dakle negirajmo izjavu koja opisuje definiciju uniformno neprekidne funkcije :[/color]
(postoji eps>0)takav da(Ad>0)(postoje x'_d,x''_d @[a,b])takvi da(|x'_d-x''_d|<d,|f(x'_d)-f(x''_d|>=eps)
[color=darkblue]ova ''nova'' izjava dopušta slobodni odabir strogo pozitivnog broja-d.
Naravno mi želimo srušiti ovu novu konkluziju implikacije iz teorema,a profesor zna kako pa ga poslušajmo i uzmimo delte oblika :[/color]
d=1/n,An@IN
[color=darkblue]čitajući gornju izjavu to znači da će za svaki n@IN postojati _barem dva_ broja x'_n i x''_n(naravno u donje indekse tih brojeva sam mogao staviti 1/n ali ovako je jednostavnije za pisati) iz segmenta [a,b] sa svojstvom da vrijedi :[/color]
|x'_n-x''_n|<1/n (*)
i
|f(x'_n)-f(x''_n)|>=eps
[color=darkblue]Ako malo bolje razmislimo mi _za svaki_ prirodni broj imamo dvije realne vrijednosti(x'_n i x'_n) što će reći da imamo dvije funkcije sa skupa prirodnih brojeva u skup IR,što će opet implicirati da takve funkcije zovemo nizovima u IR.
Dakle imamo dva niza :[/color]
{x'_n} i {x''_n} iz [a,b]
[color=darkblue]Realni brojevi x'_n i x''_n su iz segmenta što znači da su uzeti iz omeđenog(ograničenog) skupa.To implicira da mi imamo zapravo ograničene nizove.
Imamo zeleno svjetlo za korištenje doprinosa Bolzano-Weirerstrass-ovog teorema koji kaže:
Svaki ograničen niz realnih brojeva ima konvergentan podniz.
Pa ''iščupajmo'' podniz iz (recimo)niza {x'_n} :[/color]
{x'_p_n}
[color=darkblue]Kako je podniz konvergentan on mora težiti nekome broju,a kako podniz ''živi'' u segmentu [a,b] on mora težiti nekom broju iz toga segmenta.
Označimo takav broj sa c,vrijedi :[/color]
c=lim_{n->oo}x'_p_n
|x''_p_n – c|<=|x''_p_n – x'_p_n| + |x'_p_n –c |
[color=darkblue]MOJE PITANJE:Iz čega je dobivena ova relacija nejednakosti trokuta ?[/color]
[color=darkblue]Ocijenimo tu relaciju :
|x''_p_n – x'_p_n| ovaj broj ide u nulu zbog (*) iz koje se vidi da udaljenost članova niza za svaku deltu sve manja i manja kako ''odmiču'' članovi niza.
S druge strane i broj |x'_p_n –c | također ide u nulu jer je c limes podniza x'_p_n
Iz toga zaključujemo da i broj |x''_p_n – c| ide u nulu što će reći da članovi niza x''_p_n konvergiraju prema c jer je njihova udaljenost od fiksne točke c sve manja.
MOJE PITANJE:u relaciji piše ' <= ' i jednakost će biti postignuta ako imamo stacionaran niz jeli tako ?
Jer recimo da je stac.niz ima sve članove dvojke pa je dvojka i dvojka(limes tog stac.niza) jednako nula.[/color]
=>c=lim_{n->oo}x''_p_n
f je neprekidna=>neprekidna u c=>[color=darkblue]normalno je za zaključiti ako točke domene(članovi podniza) idu prema fiksnoj točki domene da će onda funkcijske vrijednosti tih točaka ići u f(c) pa jezikom limesa pišemo :[/color]
lim_{n->oo}f(x'_p_n)=f(c)=lim_{n->oo}f(x''_p_n)
=> lim_{n->oo}f(x'_p_n) - lim_{n->oo}f(x''_p_n} = 0
[color=darkblue]iskoristimo teorem o limesu razlike i imamo :[/color]
lim_{n->oo} ( f(x'_p_n) - f(x''_p_n) ) = 0
odnosno
lim_{n->oo} | f(x'_p_n) - f(x''_p_n) |=0
[color=darkblue]MOJE PITANJE:iz čega zaključim da smijem gore staviti apsolutne zagrade ?
to znači da imamo prebrojivo mnogo delti(jer delti oblika 1/n imamo prebrojivo mnogo s obzirom da je n@IN,a kako sa n idemu u oo tako udaljenost funkcijskih vrijednosti ide u nulu,što će reći da koji god pozitivan broj eps uzmem imat ću deltu za koju će udaljenost f.vrijednosti ići ispod eps-a) za koje ne vrijedi |f(x'_n)-f(x''_n)|>=eps[/color]
=>f je uniformno neprekidna
QED
PS:sve poplavljeno je moje shvaćanje pa stoga oprez.
:D
Teorem kaže:
f:[a,b] → IR neprekidna ⇒ f uniformno(jednoliko) neprekidna
Dokaz:
Pretpostavimo suprotno,dakle negirajmo izjavu koja opisuje definiciju uniformno neprekidne funkcije :
(postoji eps>0)takav da(Ad>0)(postoje x'_d,x''_d @[a,b])takvi da(|x'_d-x''_d|<d,|f(x'_d)-f(x''_d|>=eps)
ova ''nova'' izjava dopušta slobodni odabir strogo pozitivnog broja-d.
Naravno mi želimo srušiti ovu novu konkluziju implikacije iz teorema,a profesor zna kako pa ga poslušajmo i uzmimo delte oblika :
d=1/n,An@IN
čitajući gornju izjavu to znači da će za svaki n@IN postojati _barem dva_ broja x'_n i x''_n(naravno u donje indekse tih brojeva sam mogao staviti 1/n ali ovako je jednostavnije za pisati) iz segmenta [a,b] sa svojstvom da vrijedi :
|x'_n-x''_n|<1/n (*)
i
|f(x'_n)-f(x''_n)|>=eps
Ako malo bolje razmislimo mi _za svaki_ prirodni broj imamo dvije realne vrijednosti(x'_n i x'_n) što će reći da imamo dvije funkcije sa skupa prirodnih brojeva u skup IR,što će opet implicirati da takve funkcije zovemo nizovima u IR.
Dakle imamo dva niza :
{x'_n} i {x''_n} iz [a,b]
Realni brojevi x'_n i x''_n su iz segmenta što znači da su uzeti iz omeđenog(ograničenog) skupa.To implicira da mi imamo zapravo ograničene nizove.
Imamo zeleno svjetlo za korištenje doprinosa Bolzano-Weirerstrass-ovog teorema koji kaže:
Svaki ograničen niz realnih brojeva ima konvergentan podniz.
Pa ''iščupajmo'' podniz iz (recimo)niza {x'_n} :
{x'_p_n}
Kako je podniz konvergentan on mora težiti nekome broju,a kako podniz ''živi'' u segmentu [a,b] on mora težiti nekom broju iz toga segmenta.
Označimo takav broj sa c,vrijedi :
c=lim_{n→oo}x'_p_n
|x''_p_n – c|⇐|x''_p_n – x'_p_n| + |x'_p_n –c |
MOJE PITANJE:Iz čega je dobivena ova relacija nejednakosti trokuta ?
Ocijenimo tu relaciju :
|x''_p_n – x'_p_n| ovaj broj ide u nulu zbog (*) iz koje se vidi da udaljenost članova niza za svaku deltu sve manja i manja kako ''odmiču'' članovi niza.
S druge strane i broj |x'_p_n –c | također ide u nulu jer je c limes podniza x'_p_n
Iz toga zaključujemo da i broj |x''_p_n – c| ide u nulu što će reći da članovi niza x''_p_n konvergiraju prema c jer je njihova udaljenost od fiksne točke c sve manja.
MOJE PITANJE:u relaciji piše ' ⇐ ' i jednakost će biti postignuta ako imamo stacionaran niz jeli tako ?
Jer recimo da je stac.niz ima sve članove dvojke pa je dvojka i dvojka(limes tog stac.niza) jednako nula.
⇒c=lim_{n→oo}x''_p_n
f je neprekidna⇒neprekidna u c⇒normalno je za zaključiti ako točke domene(članovi podniza) idu prema fiksnoj točki domene da će onda funkcijske vrijednosti tih točaka ići u f(c) pa jezikom limesa pišemo :
lim_{n→oo}f(x'_p_n)=f(c)=lim_{n→oo}f(x''_p_n)
⇒ lim_{n→oo}f(x'_p_n) - lim_{n→oo}f(x''_p_n} = 0
iskoristimo teorem o limesu razlike i imamo :
lim_{n→oo} ( f(x'_p_n) - f(x''_p_n) ) = 0
odnosno
lim_{n→oo} | f(x'_p_n) - f(x''_p_n) |=0
MOJE PITANJE:iz čega zaključim da smijem gore staviti apsolutne zagrade ?
to znači da imamo prebrojivo mnogo delti(jer delti oblika 1/n imamo prebrojivo mnogo s obzirom da je n@IN,a kako sa n idemu u oo tako udaljenost funkcijskih vrijednosti ide u nulu,što će reći da koji god pozitivan broj eps uzmem imat ću deltu za koju će udaljenost f.vrijednosti ići ispod eps-a) za koje ne vrijedi |f(x'_n)-f(x''_n)|>=eps
⇒f je uniformno neprekidna
QED
PS:sve poplavljeno je moje shvaćanje pa stoga oprez.

_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 5:05 pet, 20. 8. 2004 Naslov: Re: Integrali-teorem Postano: 5:05 pet, 20. 8. 2004 Naslov: Re: Integrali-teorem |
    |
|
|
[quote="Vincent Van Ear"][color=green]Teorem kaže:
f:[a,b] -> IR neprekidna => f uniformno(jednoliko) neprekidna[/color]
Dokaz:
Pretpostavimo suprotno,dakle negirajmo izjavu koja opisuje definiciju uniformno neprekidne funkcije :[/quote]
[quote="Vincent Van Ear"][code:1](postoji eps>0)takav da(Ad>0)(postoje x'_d,x''_d @[a,b])takvi da(|x'_d-x''_d|<d,|f(x'_d)-f(x''_d|>=eps)[/code:1]
ova ''nova'' izjava dopušta slobodni odabir strogo pozitivnog broja-d.[/quote]
Khm :) buduci da vekya nema u blizini, proci cemo preko ove izjave ;)
[quote="Vincent Van Ear"]Naravno mi želimo srušiti ovu novu konkluziju implikacije iz teorema,a profesor zna kako pa ga poslušajmo i uzmimo delte oblika :
d=1/n,An@IN[/quote]
ok.. promatramo uredne, male delte..... tj. vaznije, definirali smo subdiviziju od n elemenata i iz proizvoljne subdivizije uzeli proizvoljne x' i x''....
[quote="Vincent Van Ear"]čitajući gornju izjavu to znači da će za svaki n@IN postojati _barem dva_ broja x'_n i x''_n(naravno u donje indekse tih brojeva sam mogao staviti 1/n ali ovako je jednostavnije za pisati) iz segmenta [a,b] sa svojstvom da vrijedi :
...dakle, prepisujemo pocetnu negaciju preko subdivizija:
[code:1]|x'_n-x''_n|<1/n (*)
i
|f(x'_n)-f(x''_n)|>=eps[/code:1]
Ako malo bolje razmislimo mi _za svaki_ prirodni broj imamo dvije realne vrijednosti(x'_n i x'[color=red]'[/color]_n) što će reći da imamo dvije funkcije sa skupa prirodnih brojeva u skup IR,što će opet implicirati da takve funkcije zovemo nizovima u IR.[/quote]
To jesu nizovi, tako smo ih definirali :)
[quote="Vincent Van Ear"]Dakle imamo dva niza :
[code:1]{x'_n} i {x''_n} iz [a,b][/code:1]
Realni brojevi x'_n i x''_n su iz segmenta što znači da su uzeti iz omeđenog(ograničenog) skupa.To implicira da mi imamo zapravo ograničene nizove.
Imamo zeleno svjetlo za korištenje doprinosa Bolzano-Weirerstrass-ovog teorema koji kaže:
Svaki ograničen niz realnih brojeva ima konvergentan podniz.
Pa ''iščupajmo'' podniz iz (recimo)niza {x'_n} :
[code:1]{x'_p_n}[/code:1]
Kako je podniz konvergentan on mora težiti nekome broju,a kako podniz ''živi'' u segmentu [a,b] on mora težiti nekom broju iz toga segmenta.
Označimo takav broj sa c,vrijedi :[/quote]
Preciznije :): omedjen niz [latex](x`_n)_n[/latex] ima konvergentan podniz i on _ _ tezi nekom broju iz svoje kodomene, koja je u nasem slucaju segment [a,b]
ps ne jednom sam dobio jezikovu juhu zbog [i]"mora"[/i] na usmenom :)
[quote="Vincent Van Ear"][code:1]c=lim_{n->oo}x'_p_n
|x''_p_n – c|<=|x''_p_n – x'_p_n| + |x'_p_n –c |[/code:1]
MOJE PITANJE:Iz čega je dobivena ova relacija nejednakosti trokuta ?[/quote]
:-s nije bas da razumijem pitanje :-s relacija trokuta, najobicnija: od tocke A do tocke B cemo prije doci ako ne idemo preko neke tocke C (ili k'_p_n ;)) :?
[quote="Vincent Van Ear"]|x''_p_n – x'_p_n| ovaj broj ide u nulu zbog (*) iz koje se vidi da udaljenost članova niza za svaku deltu sve manja i manja kako ''odmiču'' članovi niza.
S druge strane i broj |x'_p_n –c | također ide u nulu jer je c limes podniza x'_p_n
Iz toga zaključujemo da i broj |x''_p_n – c| ide u nulu što će reći da članovi niza x''_p_n konvergiraju prema c jer je njihova udaljenost od fiksne točke c sve manja.[/quote]
Mozebit da sam ja pobrkao loncice, al, ako nejednakost trokuta odozgora "nahranimo" u teorem o sendvicu :klopa: onda cemo imati:
[latex]0 \leq \lim_{n \in N} |x``_{p_n}-c| \leq \lim_{n \in N} |x``_{p_n}-x`_{p_n}| + \lim_{n \in N} |x`_{p_n}-c|=0+0[/latex]
Ah gle :) to si i ti napisao :) Ok, prvi sumand ide u 0 jer smo ga tako definirali, drugi smo sad obrazlozili
[quote="Vincent Van Ear"]MOJE PITANJE:u relaciji piše ' <= ' i jednakost će biti postignuta ako imamo stacionaran niz jeli tako ?
Jer recimo da je stac.niz ima sve članove dvojke pa je dvojka i dvojka(limes tog stac.niza) jednako nula.[/quote]
Ako imamo stacionaran niz, onda ce to biti istina, buduci da je 0=0+0 :) (razmisli, stacionaran niz => sve su isti brojevi => udaljenost izmedju _svaka_ dva clana je 0, dakle trivijalno vrijedi i nejednakost, tj jednakost :) trokuta)
Opcenito, jednakost se kod nejednakosti trokuta definiranoj sa:
[latex]d(a,c) \leq d(a,b)+d(b,c)[/latex] javlja akko je tocka b na pravcu koji prolazi tockama a i c i to izmedju tocaka a i c (incidencije, EM2).
Specijalno, u nasem slucaju, imamo "brojevni pravac", tj. 1dimenzionalni realni v.p., pa se svake tri tocke nalaze na istom pravcu :g: tako ostaje samo uvijet da broj b mora biti izmedju a i c, sto vrijedi za bilo koji (ne-nuzno-strogo) monotoni niz brojeva.
[quote="Vincent Van Ear"][code:1]=>c=lim_{n->oo}x''_p_n
f je neprekidna=>neprekidna u c=>[/code:1]
normalno je za zaključiti ako točke domene(članovi podniza) idu prema fiksnoj točki domene da će onda funkcijske vrijednosti tih točaka ići u f(c) pa jezikom limesa pišemo :[/quote]
Nije _normalno_ :-o to je poslijedica propozicije o karakterizaciji neprekidnosti preko limesa
([latex]\lim_{x \rightarrow c} f(x)=f(c) \Leftrightarrow f\_definirana\_na\_intervalu\_neprekidna\_u\_c[/latex])
[code:1]lim_{n->oo}f(x'_p_n)=f(c)=lim_{n->oo}f(x''_p_n)
=> lim_{n->oo}f(x'_p_n) - lim_{n->oo}f(x''_p_n} = 0 [/code:1]
OK, to smo ustvrdili...
[quote="Vincent Van Ear"]iskoristimo teorem o limesu razlike i imamo :
[code:1]lim_{n->oo} ( f(x'_p_n) - f(x''_p_n) ) = 0
odnosno
lim_{n->oo} | f(x'_p_n) - f(x''_p_n) |=0[/code:1]
MOJE PITANJE:iz čega zaključim da smijem gore staviti apsolutne zagrade ?[/quote]
Ako neki niz tezi u 0 tada i apsolutne vrijednosti tog niza teze u 0 :)
[quote="Vincent Van Ear"]to znači da imamo prebrojivo mnogo delti(jer delti oblika 1/n imamo prebrojivo mnogo s obzirom da je n@IN[/quote]
Neeee bas... Delti imamo neprebrojivo mnogo (delta>0, tj. realno?). Druga prica je sto je nama samo jedna delta (od tih prebrojivo mnogo koje smo promatrali) potrebna da utvrdimo netocnost one negacije sa pocetka (negacija od "svaki" jest "barem jedan", a mi trazimo kontradikciju momentalno.. ;))
[quote="Vincent Van Ear"],a kako sa n idemu u oo tako udaljenost funkcijskih vrijednosti ide u nulu,što će reći da koji god pozitivan broj eps uzmem imat ću deltu za koju će udaljenost f.vrijednosti ići ispod eps-a) za koje ne vrijedi |f(x'_n)-f(x''_n)|>=eps[/quote]
....sto je suprotno pretpostavci, dakle kontradikcija i zakljucujemo:
[code:1]=>f je uniformno neprekidna[/code:1]
[quote="Vincent Van Ear"]QED[/quote]
Jest :)
[quote="Vincent Van Ear"]PS:sve poplavljeno je moje shvaćanje pa stoga oprez.
:D[/quote]
Er... obicaj je da moderatori koriste tu boju kada nekoga lupaju po prstima :-k
ps sad mozes kvoutat formule :g:
| Vincent Van Ear (napisa): | Teorem kaže:
f:[a,b] → IR neprekidna ⇒ f uniformno(jednoliko) neprekidna
Dokaz:
Pretpostavimo suprotno,dakle negirajmo izjavu koja opisuje definiciju uniformno neprekidne funkcije : |
| Vincent Van Ear (napisa): | | Kod: | | (postoji eps>0)takav da(Ad>0)(postoje x'_d,x''_d @[a,b])takvi da(|x'_d-x''_d|<d,|f(x'_d)-f(x''_d|>=eps) |
ova ''nova'' izjava dopušta slobodni odabir strogo pozitivnog broja-d. |
Khm  buduci da vekya nema u blizini, proci cemo preko ove izjave buduci da vekya nema u blizini, proci cemo preko ove izjave 
| Vincent Van Ear (napisa): | Naravno mi želimo srušiti ovu novu konkluziju implikacije iz teorema,a profesor zna kako pa ga poslušajmo i uzmimo delte oblika :
d=1/n,An@IN |
ok.. promatramo uredne, male delte..... tj. vaznije, definirali smo subdiviziju od n elemenata i iz proizvoljne subdivizije uzeli proizvoljne x' i x''....
| Vincent Van Ear (napisa): | čitajući gornju izjavu to znači da će za svaki n@IN postojati _barem dva_ broja x'_n i x''_n(naravno u donje indekse tih brojeva sam mogao staviti 1/n ali ovako je jednostavnije za pisati) iz segmenta [a,b] sa svojstvom da vrijedi :
...dakle, prepisujemo pocetnu negaciju preko subdivizija:
| Kod: | |x'_n-x''_n|<1/n (*)
i
|f(x'_n)-f(x''_n)|>=eps |
Ako malo bolje razmislimo mi _za svaki_ prirodni broj imamo dvije realne vrijednosti(x'_n i x''_n) što će reći da imamo dvije funkcije sa skupa prirodnih brojeva u skup IR,što će opet implicirati da takve funkcije zovemo nizovima u IR. |
To jesu nizovi, tako smo ih definirali 
| Vincent Van Ear (napisa): | Dakle imamo dva niza :
| Kod: | | {x'_n} i {x''_n} iz [a,b] |
Realni brojevi x'_n i x''_n su iz segmenta što znači da su uzeti iz omeđenog(ograničenog) skupa.To implicira da mi imamo zapravo ograničene nizove.
Imamo zeleno svjetlo za korištenje doprinosa Bolzano-Weirerstrass-ovog teorema koji kaže:
Svaki ograničen niz realnih brojeva ima konvergentan podniz.
Pa ''iščupajmo'' podniz iz (recimo)niza {x'_n} :
Kako je podniz konvergentan on mora težiti nekome broju,a kako podniz ''živi'' u segmentu [a,b] on mora težiti nekom broju iz toga segmenta.
Označimo takav broj sa c,vrijedi : |
Preciznije  : omedjen niz : omedjen niz 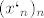 ima konvergentan podniz i on _ _ tezi nekom broju iz svoje kodomene, koja je u nasem slucaju segment [a,b] ima konvergentan podniz i on _ _ tezi nekom broju iz svoje kodomene, koja je u nasem slucaju segment [a,b]
ps ne jednom sam dobio jezikovu juhu zbog "mora" na usmenom 
| Vincent Van Ear (napisa): | | Kod: | c=lim_{n->oo}x'_p_n
|x''_p_n – c|<=|x''_p_n – x'_p_n| + |x'_p_n –c | |
MOJE PITANJE:Iz čega je dobivena ova relacija nejednakosti trokuta ? |
 nije bas da razumijem pitanje nije bas da razumijem pitanje  relacija trokuta, najobicnija: od tocke A do tocke B cemo prije doci ako ne idemo preko neke tocke C (ili k'_p_n relacija trokuta, najobicnija: od tocke A do tocke B cemo prije doci ako ne idemo preko neke tocke C (ili k'_p_n  ) ) 
| Vincent Van Ear (napisa): | |x''_p_n – x'_p_n| ovaj broj ide u nulu zbog (*) iz koje se vidi da udaljenost članova niza za svaku deltu sve manja i manja kako ''odmiču'' članovi niza.
S druge strane i broj |x'_p_n –c | također ide u nulu jer je c limes podniza x'_p_n
Iz toga zaključujemo da i broj |x''_p_n – c| ide u nulu što će reći da članovi niza x''_p_n konvergiraju prema c jer je njihova udaljenost od fiksne točke c sve manja. |
Mozebit da sam ja pobrkao loncice, al, ako nejednakost trokuta odozgora "nahranimo" u teorem o sendvicu  onda cemo imati: onda cemo imati:
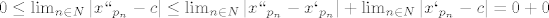
Ah gle  to si i ti napisao to si i ti napisao  Ok, prvi sumand ide u 0 jer smo ga tako definirali, drugi smo sad obrazlozili Ok, prvi sumand ide u 0 jer smo ga tako definirali, drugi smo sad obrazlozili
| Vincent Van Ear (napisa): | MOJE PITANJE:u relaciji piše ' ⇐ ' i jednakost će biti postignuta ako imamo stacionaran niz jeli tako ?
Jer recimo da je stac.niz ima sve članove dvojke pa je dvojka i dvojka(limes tog stac.niza) jednako nula. |
Ako imamo stacionaran niz, onda ce to biti istina, buduci da je 0=0+0  (razmisli, stacionaran niz ⇒ sve su isti brojevi ⇒ udaljenost izmedju _svaka_ dva clana je 0, dakle trivijalno vrijedi i nejednakost, tj jednakost (razmisli, stacionaran niz ⇒ sve su isti brojevi ⇒ udaljenost izmedju _svaka_ dva clana je 0, dakle trivijalno vrijedi i nejednakost, tj jednakost  trokuta) trokuta)
Opcenito, jednakost se kod nejednakosti trokuta definiranoj sa:
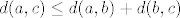 javlja akko je tocka b na pravcu koji prolazi tockama a i c i to izmedju tocaka a i c (incidencije, EM2). javlja akko je tocka b na pravcu koji prolazi tockama a i c i to izmedju tocaka a i c (incidencije, EM2).
Specijalno, u nasem slucaju, imamo "brojevni pravac", tj. 1dimenzionalni realni v.p., pa se svake tri tocke nalaze na istom pravcu  tako ostaje samo uvijet da broj b mora biti izmedju a i c, sto vrijedi za bilo koji (ne-nuzno-strogo) monotoni niz brojeva. tako ostaje samo uvijet da broj b mora biti izmedju a i c, sto vrijedi za bilo koji (ne-nuzno-strogo) monotoni niz brojeva.
| Vincent Van Ear (napisa): | | Kod: | =>c=lim_{n->oo}x''_p_n
f je neprekidna=>neprekidna u c=> |
normalno je za zaključiti ako točke domene(članovi podniza) idu prema fiksnoj točki domene da će onda funkcijske vrijednosti tih točaka ići u f(c) pa jezikom limesa pišemo : |
Nije _normalno_  to je poslijedica propozicije o karakterizaciji neprekidnosti preko limesa to je poslijedica propozicije o karakterizaciji neprekidnosti preko limesa
(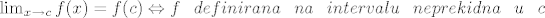 ) )
| Kod: | lim_{n->oo}f(x'_p_n)=f(c)=lim_{n->oo}f(x''_p_n)
=> lim_{n->oo}f(x'_p_n) - lim_{n->oo}f(x''_p_n} = 0 |
OK, to smo ustvrdili...
| Vincent Van Ear (napisa): | iskoristimo teorem o limesu razlike i imamo :
| Kod: | lim_{n->oo} ( f(x'_p_n) - f(x''_p_n) ) = 0
odnosno
lim_{n->oo} | f(x'_p_n) - f(x''_p_n) |=0 |
MOJE PITANJE:iz čega zaključim da smijem gore staviti apsolutne zagrade ? |
Ako neki niz tezi u 0 tada i apsolutne vrijednosti tog niza teze u 0 
| Vincent Van Ear (napisa): | | to znači da imamo prebrojivo mnogo delti(jer delti oblika 1/n imamo prebrojivo mnogo s obzirom da je n@IN |
Neeee bas... Delti imamo neprebrojivo mnogo (delta>0, tj. realno?). Druga prica je sto je nama samo jedna delta (od tih prebrojivo mnogo koje smo promatrali) potrebna da utvrdimo netocnost one negacije sa pocetka (negacija od "svaki" jest "barem jedan", a mi trazimo kontradikciju momentalno..  ) )
| Vincent Van Ear (napisa): | | ,a kako sa n idemu u oo tako udaljenost funkcijskih vrijednosti ide u nulu,što će reći da koji god pozitivan broj eps uzmem imat ću deltu za koju će udaljenost f.vrijednosti ići ispod eps-a) za koje ne vrijedi |f(x'_n)-f(x''_n)|>=eps |
....sto je suprotno pretpostavci, dakle kontradikcija i zakljucujemo:
| Kod: | | =>f je uniformno neprekidna |
| Vincent Van Ear (napisa): | | QED |
Jest 
| Vincent Van Ear (napisa): | PS:sve poplavljeno je moje shvaćanje pa stoga oprez.
 |
Er... obicaj je da moderatori koriste tu boju kada nekoga lupaju po prstima 
ps sad mozes kvoutat formule 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 15:23 pet, 20. 8. 2004 Naslov: Postano: 15:23 pet, 20. 8. 2004 Naslov: |
    |
|
|
[quote]Khm buduci da vekya nema u blizini, proci cemo preko ove izjave [/quote]
Slobodno ti reci sve što ti je na pameti,ja volim ''čuškice'' jer me potiču na preciznije razmišljanje i pisanje;)
Hočeš mi na fin način kazati da mi fali onaj 'i' u negaciji implikacije?Ako ne onda mi ne moraš ništa reći! :mrgreen: joke! :wink:
[quote]tj. vaznije, definirali smo subdiviziju od n elemenata i iz proizvoljne subdivizije uzeli proizvoljne x' i x''....[/quote]
ovo nisam shvatio :?:
Što mi želiš reći i čemu mi uopće treba saznanje u subdiviziji u ovom dokazu ?
[quote]To jesu nizovi, tako smo ih definirali [/quote]
Nečeg sam se još sijetio:
Negacijska izjava mi jamči da postoje bar dva realna broja iz segmenta [a,b] za koje vrijedi da su manji od 1/n za n@IN.
Naravno,mi smo u IR pa takvih brojeva ima neprebrojivo mnogo(na najmanjoj zamislivoj dužini realnog pravca ''stanuje'' neprebrojivo mnogo brojeva) što će reći da ja jednom prirodnom broju _mogu_ pridružiti neprebrojivo mnogo realnih vrijednosti _ali_ ja pridružujem samo jednu-jedinu jer želim funkciju sa IN u IR.
Jesam li točan?
btw,da vrijedi
za An@IN , postoje x'_n,x''_n@[a,b] za [a,b] iz IR vrijedi |x'_n-x''_n|<1/n
može se zaključiti da je istina(osim iz izjave-negacije uniformne neprekidnosti) jer je skup IR gust(nema ''rupa'') pa koliko god malu udaljenost mi daš naći ću dva realna broja koji su manji od nje.
[quote]ps ne jednom sam dobio jezikovu juhu zbog "mora" na usmenom [/quote]
samo ti prostri na ''dekicu'' sve što imaš,dapače. :mrgreen:
[quote] nije bas da razumijem pitanje [/quote]
Zašto su ''akteri'' relacije trokuta(x''_p_n,c,x'_p_n) baš tako sortirani.
Jasna mi je relacija ali kako u nju slažem aktere.
[quote]relacija trokuta, najobicnija: od tocke A do tocke B cemo prije doci ako ne idemo preko neke tocke C (ili k'_p_n ) [/quote]
slikovito,nice.
[quote]Mozebit da sam ja pobrkao loncice, al, ako nejednakost trokuta odozgora "nahranimo" u teorem o sendvicu onda cemo imati:
Ah gle to si i ti napisao Ok, prvi sumand ide u 0 jer smo ga tako definirali, drugi smo sad obrazlozili
[/quote]
Kako bi prof Šikić bio sretan da vidi da ovako obrazložim relaciju… :mrgreen:
[quote]Nije _normalno_ to je poslijedica propozicije o karakterizaciji neprekidnosti preko limesa ( [/quote]
Isuse,kako se nisam toga sjetio? :weee:
Vjeruj mi,znao sam da ću zvučati šlampavo sa svojom rečenicom gore.
Kako sam looooš. :cry:
[quote]Neeee bas... Delti imamo neprebrojivo mnogo (delta>0, tj. realno?). Druga prica je sto je nama samo jedna delta (od tih prebrojivo mnogo koje smo promatrali) potrebna da utvrdimo netocnost one negacije sa pocetka (negacija od "svaki" jest "barem jedan", a mi trazimo kontradikciju momentalno.. )[/quote]
Ok,btw mori me upitnik kraj riječi 'realno',što mi želiš natuknuti?
Da svaki strogo pozitivan broj je sigurno realan,ali,to nigdje ne piše,uglavnom-the truth is out there… ;)
[quote]Er... obicaj je da moderatori koriste tu boju kada nekoga lupaju po prstima [/quote]
kud baš meni fejvrit,ccc… :mrgreen:
A kaj bi ja mogel bit moderator? :rotfl: :wink:
| Citat: | | Khm buduci da vekya nema u blizini, proci cemo preko ove izjave |
Slobodno ti reci sve što ti je na pameti,ja volim ''čuškice'' jer me potiču na preciznije razmišljanje i pisanje;)
Hočeš mi na fin način kazati da mi fali onaj 'i' u negaciji implikacije?Ako ne onda mi ne moraš ništa reći!  joke! joke! 
| Citat: | | tj. vaznije, definirali smo subdiviziju od n elemenata i iz proizvoljne subdivizije uzeli proizvoljne x' i x''.... |
ovo nisam shvatio 
Što mi želiš reći i čemu mi uopće treba saznanje u subdiviziji u ovom dokazu ?
| Citat: | | To jesu nizovi, tako smo ih definirali |
Nečeg sam se još sijetio:
Negacijska izjava mi jamči da postoje bar dva realna broja iz segmenta [a,b] za koje vrijedi da su manji od 1/n za n@IN.
Naravno,mi smo u IR pa takvih brojeva ima neprebrojivo mnogo(na najmanjoj zamislivoj dužini realnog pravca ''stanuje'' neprebrojivo mnogo brojeva) što će reći da ja jednom prirodnom broju _mogu_ pridružiti neprebrojivo mnogo realnih vrijednosti _ali_ ja pridružujem samo jednu-jedinu jer želim funkciju sa IN u IR.
Jesam li točan?
btw,da vrijedi
za An@IN , postoje x'_n,x''_n@[a,b] za [a,b] iz IR vrijedi |x'_n-x''_n|<1/n
može se zaključiti da je istina(osim iz izjave-negacije uniformne neprekidnosti) jer je skup IR gust(nema ''rupa'') pa koliko god malu udaljenost mi daš naći ću dva realna broja koji su manji od nje.
| Citat: | | ps ne jednom sam dobio jezikovu juhu zbog "mora" na usmenom |
samo ti prostri na ''dekicu'' sve što imaš,dapače. 
| Citat: | | nije bas da razumijem pitanje |
Zašto su ''akteri'' relacije trokuta(x''_p_n,c,x'_p_n) baš tako sortirani.
Jasna mi je relacija ali kako u nju slažem aktere.
| Citat: | | relacija trokuta, najobicnija: od tocke A do tocke B cemo prije doci ako ne idemo preko neke tocke C (ili k'_p_n ) |
slikovito,nice.
| Citat: | Mozebit da sam ja pobrkao loncice, al, ako nejednakost trokuta odozgora "nahranimo" u teorem o sendvicu onda cemo imati:
Ah gle to si i ti napisao Ok, prvi sumand ide u 0 jer smo ga tako definirali, drugi smo sad obrazlozili
|
Kako bi prof Šikić bio sretan da vidi da ovako obrazložim relaciju… 
| Citat: | | Nije _normalno_ to je poslijedica propozicije o karakterizaciji neprekidnosti preko limesa ( |
Isuse,kako se nisam toga sjetio? 
Vjeruj mi,znao sam da ću zvučati šlampavo sa svojom rečenicom gore.
Kako sam looooš. 
| Citat: | | Neeee bas... Delti imamo neprebrojivo mnogo (delta>0, tj. realno?). Druga prica je sto je nama samo jedna delta (od tih prebrojivo mnogo koje smo promatrali) potrebna da utvrdimo netocnost one negacije sa pocetka (negacija od "svaki" jest "barem jedan", a mi trazimo kontradikciju momentalno.. ) |
Ok,btw mori me upitnik kraj riječi 'realno',što mi želiš natuknuti?
Da svaki strogo pozitivan broj je sigurno realan,ali,to nigdje ne piše,uglavnom-the truth is out there… 
| Citat: | | Er... obicaj je da moderatori koriste tu boju kada nekoga lupaju po prstima |
kud baš meni fejvrit,ccc… 
A kaj bi ja mogel bit moderator?  
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 15:56 sub, 21. 8. 2004 Naslov: Postano: 15:56 sub, 21. 8. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"]Slobodno ti reci sve što ti je na pameti,ja volim ''čuškice'' jer me potiču na preciznije razmišljanje i pisanje;)[/quote]
Don't be so hard on yourself, ako si ti takav, sta cu onda ja cinit ;) ?
[quote="Vincent Van Ear"]Hočeš mi na fin način kazati da mi fali onaj 'i' u negaciji implikacije?Ako ne onda mi ne moraš ništa reći! :mrgreen: joke! :wink: [/quote]
Imam dobro oko za promasiti takve stvari, ako ne vicem, to ne znaci da si u pravu ;)
[quote="Vincent Van Ear"][quote]tj. vaznije, definirali smo subdiviziju od n elemenata i iz proizvoljne subdivizije uzeli proizvoljne x' i x''....[/quote]
ovo nisam shvatio :?:
Što mi želiš reći i čemu mi uopće treba saznanje u subdiviziji u ovom dokazu ?[/quote]
Mozda je to samo moja interpretacija recenoga ;) U stvari, uzeli smo proizvoljni interval velicine 1/n i unutar njega proizvoljne x' i x'', al sam, buduci da smo u kontekstu integriranja, to nazvao subdivizijama :oops: :)
[quote="Vincent Van Ear"]Nečeg sam se još sijetio:
Negacijska izjava mi jamči da [color=red]postoje bar dva realna broja iz segmenta [a,b] za koje vrijedi da su manji od 1/n za n@IN.[/color][/quote]
Mislis, "..da su udaljeni za manje od 1/n", nadam se :)
[quote="Vincent Van Ear"]Naravno,mi smo u IR pa takvih brojeva ima neprebrojivo mnogo(na najmanjoj zamislivoj dužini realnog pravca ''stanuje'' neprebrojivo mnogo brojeva) što će reći da ja jednom prirodnom broju _mogu_ pridružiti neprebrojivo mnogo realnih vrijednosti _ali_ ja pridružujem samo jednu-jedinu jer želim funkciju sa IN u IR.
Jesam li točan?[/quote]
:lol: da, jesi :D :lol: al ne shvacam sto pokusavas reci :) Naravno, ako funkcija ide u |R (sa kojegod domene), ima na raspolaganju neprebrojivo mnogo clanova kodomene da u njeg nesto preslika, i... Naravno.. da bi to bila funkcija, nasem clanu domene mozemo preslikati _tocno_ jedan clan kodomene, ako je to ono sto si htio reci?
[quote="Vincent Van Ear"]btw,da vrijedi
[latex] \forall n \in N , \exists x`_n,x``_n \in [a,b] ~ t.d. ~ |x`_n-x``_n|<1/n[/latex]
može se zaključiti da je istina(osim iz izjave-negacije uniformne neprekidnosti) jer je skup IR gust(nema ''rupa'') pa koliko god malu udaljenost mi daš naći ću dva realna broja koji su manji od nje.[/quote]
Naravno, to je relativno jednostavna poslijedica Arhimedovog aksioma(teorema, kakogod - na>b - btw, OT, ne zaboravi to ako te ikada pitaju konvergentnost od 1/n (a vjerovatno hoce)). Imas nesto na umu?
[quote="Vincent Van Ear"]Zašto su ''akteri'' relacije trokuta(x''_p_n,c,x'_p_n) baš tako sortirani.
Jasna mi je relacija ali kako u nju slažem aktere.[/quote]
Hm :) Idemo od pocetka, imamo nesto sto zovemo funkcijom metrike. Funkcija metrike paru tocaka pridruzuje "udaljenost" medju njima, preciznije, fja metrike mora imati slijedeca svojstva (pa ju definiramo na slijedeci nacin):
[latex]~S\_je\_skup\_t.d. ~S \neq \emptyset~, ~d:S \times S \rightarrow R \\
(M1)~ ~d(A,B) \geq 0 ~ ~ \forall A,B \in S \\
(M2)~ ~ d(A,B)=0 \Leftrightarrow A=B \\
(M3)~ ~ d(A,B)=d(B,A) ~ ~ \forall A,B \in S \\
(M4)~ ~ d(A,C) \leq d(A,B)+d(B,C) ~ ~ \forall A,B,C \in S[/latex]
[i](vjerujem da ces se snaci ako pozelis kvoutat samo dio ovih "formula" gore (\\ je delimiter za red), kodovi su vrlo citljivi)[/i]
..i, ako malo bolje pogledas, funkcija |a-b| je dobra fja udaljenosti na |R, pa (M4) mozemo raspisati kao:
[latex]d(a,b):=|b-a| \\
d(x``, c) \leq d(x``, x`)+d(x`, c)[/latex]
gdje je x' jedna s(p)retno odabrana treca tocka :)
btw: ako je skup S iz gornje definicije neki vektorski prostor (V), onda uredjen par v.p. i metrike (V, d) nazivamo metrickim prostorom. (|R, | |) jest jedan primjer metrickog prostora. Ovo ti ne bi trebalo biti nista novo ako vladas LA2?
[quote="Vincent Van Ear"][quote]Mozebit da sam ja pobrkao loncice, al, ako nejednakost trokuta odozgora "nahranimo" u teorem o sendvicu onda cemo imati: [/quote]
Kako bi prof Šikić bio sretan da vidi da ovako obrazložim relaciju… :mrgreen:[/quote]
:OT: prof. Sikic (Tomislav) voli sendvice i teoreme o njima, prica se :D
[quote="Vincent Van Ear"]Ok,btw mori me upitnik kraj riječi 'realno',što mi želiš natuknuti?[/quote]
Upitnik je tu da naglasi da se radi o realnom broju i da malo razmislis o tom =>
[quote="Vincent Van Ear"]Da svaki strogo pozitivan broj je sigurno realan,ali,to nigdje ne piše,uglavnom-the truth is out there… ;)[/quote]
=> eto vidis :g:
[quote="Vincent Van Ear"]A kaj bi ja mogel bit moderator? :rotfl: :wink:[/quote]
Moli vsegu :g:
| Vincent Van Ear (napisa): | | Slobodno ti reci sve što ti je na pameti,ja volim ''čuškice'' jer me potiču na preciznije razmišljanje i pisanje;) |
Don't be so hard on yourself, ako si ti takav, sta cu onda ja cinit  ? ?
| Vincent Van Ear (napisa): | Hočeš mi na fin način kazati da mi fali onaj 'i' u negaciji implikacije?Ako ne onda mi ne moraš ništa reći!  joke! joke!  |
Imam dobro oko za promasiti takve stvari, ako ne vicem, to ne znaci da si u pravu 
| Vincent Van Ear (napisa): | | Citat: | | tj. vaznije, definirali smo subdiviziju od n elemenata i iz proizvoljne subdivizije uzeli proizvoljne x' i x''.... |
ovo nisam shvatio 
Što mi želiš reći i čemu mi uopće treba saznanje u subdiviziji u ovom dokazu ? |
Mozda je to samo moja interpretacija recenoga  U stvari, uzeli smo proizvoljni interval velicine 1/n i unutar njega proizvoljne x' i x'', al sam, buduci da smo u kontekstu integriranja, to nazvao subdivizijama U stvari, uzeli smo proizvoljni interval velicine 1/n i unutar njega proizvoljne x' i x'', al sam, buduci da smo u kontekstu integriranja, to nazvao subdivizijama  
| Vincent Van Ear (napisa): | Nečeg sam se još sijetio:
Negacijska izjava mi jamči da postoje bar dva realna broja iz segmenta [a,b] za koje vrijedi da su manji od 1/n za n@IN. |
Mislis, "..da su udaljeni za manje od 1/n", nadam se 
| Vincent Van Ear (napisa): | Naravno,mi smo u IR pa takvih brojeva ima neprebrojivo mnogo(na najmanjoj zamislivoj dužini realnog pravca ''stanuje'' neprebrojivo mnogo brojeva) što će reći da ja jednom prirodnom broju _mogu_ pridružiti neprebrojivo mnogo realnih vrijednosti _ali_ ja pridružujem samo jednu-jedinu jer želim funkciju sa IN u IR.
Jesam li točan? |
 da, jesi da, jesi   al ne shvacam sto pokusavas reci al ne shvacam sto pokusavas reci  Naravno, ako funkcija ide u |R (sa kojegod domene), ima na raspolaganju neprebrojivo mnogo clanova kodomene da u njeg nesto preslika, i... Naravno.. da bi to bila funkcija, nasem clanu domene mozemo preslikati _tocno_ jedan clan kodomene, ako je to ono sto si htio reci? Naravno, ako funkcija ide u |R (sa kojegod domene), ima na raspolaganju neprebrojivo mnogo clanova kodomene da u njeg nesto preslika, i... Naravno.. da bi to bila funkcija, nasem clanu domene mozemo preslikati _tocno_ jedan clan kodomene, ako je to ono sto si htio reci?
| Vincent Van Ear (napisa): | btw,da vrijedi
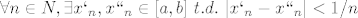
može se zaključiti da je istina(osim iz izjave-negacije uniformne neprekidnosti) jer je skup IR gust(nema ''rupa'') pa koliko god malu udaljenost mi daš naći ću dva realna broja koji su manji od nje. |
Naravno, to je relativno jednostavna poslijedica Arhimedovog aksioma(teorema, kakogod - na>b - btw, OT, ne zaboravi to ako te ikada pitaju konvergentnost od 1/n (a vjerovatno hoce)). Imas nesto na umu?
| Vincent Van Ear (napisa): | Zašto su ''akteri'' relacije trokuta(x''_p_n,c,x'_p_n) baš tako sortirani.
Jasna mi je relacija ali kako u nju slažem aktere. |
Hm  Idemo od pocetka, imamo nesto sto zovemo funkcijom metrike. Funkcija metrike paru tocaka pridruzuje "udaljenost" medju njima, preciznije, fja metrike mora imati slijedeca svojstva (pa ju definiramo na slijedeci nacin): Idemo od pocetka, imamo nesto sto zovemo funkcijom metrike. Funkcija metrike paru tocaka pridruzuje "udaljenost" medju njima, preciznije, fja metrike mora imati slijedeca svojstva (pa ju definiramo na slijedeci nacin):
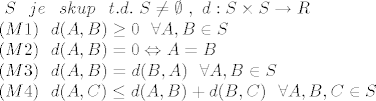
(vjerujem da ces se snaci ako pozelis kvoutat samo dio ovih "formula" gore (\\ je delimiter za red), kodovi su vrlo citljivi)
..i, ako malo bolje pogledas, funkcija |a-b| je dobra fja udaljenosti na |R, pa (M4) mozemo raspisati kao:
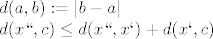
gdje je x' jedna s(p)retno odabrana treca tocka 
btw: ako je skup S iz gornje definicije neki vektorski prostor (V), onda uredjen par v.p. i metrike (V, d) nazivamo metrickim prostorom. (|R, | |) jest jedan primjer metrickog prostora. Ovo ti ne bi trebalo biti nista novo ako vladas LA2?
| Vincent Van Ear (napisa): | | Citat: | | Mozebit da sam ja pobrkao loncice, al, ako nejednakost trokuta odozgora "nahranimo" u teorem o sendvicu onda cemo imati: |
Kako bi prof Šikić bio sretan da vidi da ovako obrazložim relaciju…  |
 prof. Sikic (Tomislav) voli sendvice i teoreme o njima, prica se prof. Sikic (Tomislav) voli sendvice i teoreme o njima, prica se 
| Vincent Van Ear (napisa): | | Ok,btw mori me upitnik kraj riječi 'realno',što mi želiš natuknuti? |
Upitnik je tu da naglasi da se radi o realnom broju i da malo razmislis o tom ⇒
| Vincent Van Ear (napisa): | Da svaki strogo pozitivan broj je sigurno realan,ali,to nigdje ne piše,uglavnom-the truth is out there…  |
⇒ eto vidis 
| Vincent Van Ear (napisa): | A kaj bi ja mogel bit moderator?   |
Moli vsegu 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 17:40 sub, 21. 8. 2004 Naslov: Postano: 17:40 sub, 21. 8. 2004 Naslov: |
    |
|
|
[quote]Mozda je to samo moja interpretacija recenoga U stvari, uzeli smo proizvoljni interval velicine 1/n i unutar njega proizvoljne x' i x'', al sam, buduci da smo u kontekstu integriranja, to nazvao subdivizijama [/quote]
Ok.
[quote]Mislis, "..da su udaljeni za manje od 1/n", nadam se[/quote]
Tako je.
[quote] da, jesi [/quote]
:lol:
[quote]al ne shvacam sto pokusavas reci [/quote]
ma samo potvrđujem svoju misao. :wink:
[quote]Naravno, to je relativno jednostavna poslijedica Arhimedovog aksioma(teorema, kakogod - na>b - btw, OT, ne zaboravi to ako te ikada pitaju konvergentnost od 1/n (a vjerovatno hoce)). Imas nesto na umu?[/quote]
again,potvrda vlastite misli,hm,volim da mi netko potvrdi misao jer je ona,hm,često-iskrivljena,hm. :shock:
[quote]Hm Idemo od pocetka, imamo nesto sto zovemo funkcijom metrike. Funkcija metrike paru tocaka pridruzuje "udaljenost" medju njima, preciznije, fja metrike mora imati slijedeca svojstva (pa ju definiramo na slijedeci nacin):
(vjerujem da ces se snaci ako pozelis kvoutat samo dio ovih "formula" gore (\\ je delimiter za red), kodovi su vrlo citljivi)
..i, ako malo bolje pogledas, funkcija |a-b| je dobra fja udaljenosti na |R, pa (M4) mozemo raspisati kao:
gdje je x' jedna s(p)retno odabrana treca tocka
btw: ako je skup S iz gornje definicije neki vektorski prostor (V), onda uredjen par v.p. i metrike (V, d) nazivamo metrickim prostorom. (|R, | |) jest jedan primjer metrickog prostora.
[/quote]
Hvala ti za trud. :wink:
Hm,znaš što me buni,imam x',x'' i c i sada njih počinjem ''slagati'' u nejednakost trokuta,kako ih slažem,kako zaključujem da će mi modul |x''_p_n| biti slijeva,a suma modula |x''_p_n – x'_p_n| i |x'_p_n –c | zdesna?
Što me vodi u toj ''igri slaganja'' da ne griješim gdje ću koji modul staviti s obzirom na nejednakost ?
Vidim tu relaciju i jasno mi je koje informacije mi ''odašilje'' ali zanima me kako je ta relacija ''sklepana'',kako su moduli našli svoje mjesto u njoj?
I još nešto starijega :
ti si ovaj izraz:
|x''_p_n – c|<=|x''_p_n – x'_p_n| + |x'_p_n –c |
pretvorio u ovaj:
lim_{n->oo}|x''_p_n – c|<=lim_{n->oo}|x''_p_n – x'_p_n| + lim_{n->oo}|x'_p_n –c |
Kako ja tu radnju precizno interpretiram,sigurno ne ukoliko kažem:
djelujemo limesom na relaciju(tako izgleda)?
Kada uopće limes smije ''napadati'' jednadžbe ?
[/quote]
| Citat: | | Mozda je to samo moja interpretacija recenoga U stvari, uzeli smo proizvoljni interval velicine 1/n i unutar njega proizvoljne x' i x'', al sam, buduci da smo u kontekstu integriranja, to nazvao subdivizijama |
Ok.
| Citat: | | Mislis, "..da su udaljeni za manje od 1/n", nadam se |
Tako je.

| Citat: | | al ne shvacam sto pokusavas reci |
ma samo potvrđujem svoju misao. 
| Citat: | | Naravno, to je relativno jednostavna poslijedica Arhimedovog aksioma(teorema, kakogod - na>b - btw, OT, ne zaboravi to ako te ikada pitaju konvergentnost od 1/n (a vjerovatno hoce)). Imas nesto na umu? |
again,potvrda vlastite misli,hm,volim da mi netko potvrdi misao jer je ona,hm,često-iskrivljena,hm. 
| Citat: | Hm Idemo od pocetka, imamo nesto sto zovemo funkcijom metrike. Funkcija metrike paru tocaka pridruzuje "udaljenost" medju njima, preciznije, fja metrike mora imati slijedeca svojstva (pa ju definiramo na slijedeci nacin):
(vjerujem da ces se snaci ako pozelis kvoutat samo dio ovih "formula" gore (\\ je delimiter za red), kodovi su vrlo citljivi)
..i, ako malo bolje pogledas, funkcija |a-b| je dobra fja udaljenosti na |R, pa (M4) mozemo raspisati kao:
gdje je x' jedna s(p)retno odabrana treca tocka
btw: ako je skup S iz gornje definicije neki vektorski prostor (V), onda uredjen par v.p. i metrike (V, d) nazivamo metrickim prostorom. (|R, | |) jest jedan primjer metrickog prostora.
|
Hvala ti za trud. 
Hm,znaš što me buni,imam x',x'' i c i sada njih počinjem ''slagati'' u nejednakost trokuta,kako ih slažem,kako zaključujem da će mi modul |x''_p_n| biti slijeva,a suma modula |x''_p_n – x'_p_n| i |x'_p_n –c | zdesna?
Što me vodi u toj ''igri slaganja'' da ne griješim gdje ću koji modul staviti s obzirom na nejednakost ?
Vidim tu relaciju i jasno mi je koje informacije mi ''odašilje'' ali zanima me kako je ta relacija ''sklepana'',kako su moduli našli svoje mjesto u njoj?
I još nešto starijega :
ti si ovaj izraz:
|x''_p_n – c|⇐|x''_p_n – x'_p_n| + |x'_p_n –c |
pretvorio u ovaj:
lim_{n→oo}|x''_p_n – c|⇐lim_{n→oo}|x''_p_n – x'_p_n| + lim_{n→oo}|x'_p_n –c |
Kako ja tu radnju precizno interpretiram,sigurno ne ukoliko kažem:
djelujemo limesom na relaciju(tako izgleda)?
Kada uopće limes smije ''napadati'' jednadžbe ?
[/quote]
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 23:29 sub, 21. 8. 2004 Naslov: Postano: 23:29 sub, 21. 8. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"]Hm,znaš što me buni,imam x',x'' i c i sada njih počinjem ''slagati'' u nejednakost trokuta,kako ih slažem,kako zaključujem da će mi modul |x''_p_n| biti slijeva,a suma modula |x''_p_n – x'_p_n| i |x'_p_n –c | zdesna?
Što me vodi u toj ''igri slaganja'' da ne griješim gdje ću koji modul staviti s obzirom na nejednakost ?
Vidim tu relaciju i jasno mi je koje informacije mi ''odašilje'' ali zanima me kako je ta relacija ''sklepana'',kako su moduli našli svoje mjesto u njoj?[/quote]
Pa.. Zelis dokazati da "podnizi" (ne da mi se pisat indekse) od x' i x'' teze ka istoj vrijednosti (to sto oni samo po sebi teze jedan drugom ti za sada ne govori mnogo i o njihovim fjskim vrijednostima, tu ulazi relacija trokuta). Nasao si da x' ima podniz koji konvergira i rekao da je taj limes=c. Da bi dokazao uniformnu neprekidnost, tj. u nasem slucaju, kontradikciju, moras dokazati da x'' (a dakle i njegove funkcijske vrijednosti) isto teze ka c (tj, f(c), tj. f(x') i f(x'') imaju isti limes).
Sta imamo?
(1) znamo udaljenost od x'' do x'
(2) znamo i udaljenost od x' do c
(3) ono sto ne znamo je udaljenost x'' do c (da mozemo primijeniti onu propoziciju o limesu neprekidne fje), sto je, vidi s(p)retnog cuda :) kraca udaljenost od te kada bi npr. isli od x'' do c preko neke trece tocke, npr. x' :)
I sada drugi dio:
[quote="Vincent Van Ear"]I još nešto starijega :
ti si ovaj izraz:
[latex] |x``_{p_n} - c| \leq |x``_{p_n} - x`_{p_n}| + |x`_{p_n} -c | [/latex]
pretvorio u ovaj:
[latex]0 \leq \lim_{n \in N} |x``_{p_n}-c| \leq \lim_{n \in N} |x``_{p_n}-x`_{p_n}| + \lim_{n \in N} |x`_{p_n}-c|=0+0[/latex]
Kako ja tu radnju precizno interpretiram,sigurno ne ukoliko kažem:
djelujemo limesom na relaciju(tako izgleda)?[/quote]
Formalno: imamo nejednakost:
[latex] 0 < |x``_{p_n} - c| \leq |x``_{p_n} - x`_{p_n}| + |x`_{p_n} -c | [/latex]
prvo cu promotrit desni dio nejednakosti, tu je stvar dosta cista (x' po definiciji tezi u c a udaljenost od x' do x'' je manja od 1/n tako da:
[latex](!) \lim_{n \in N} |x`_{p_n}-c|=0 \\
0 \leq \lim_{n \in N} |x``_{p_n}-x`_{p_n}| \leq \lim_{n \in N}1/n =0
\Rightarrow \lim_{n \in N} |x``_{p_n}-x`_{p_n}|=0 \\
\Rightarrow^{po\_prop\_o\_sumi\_limesa} \lim_{n \in N} [|x``_{p_n}-x`_{p_n}|+|x`_{p_n}-c| ] = 0[/latex]
Dakle, opet, primijenom tm. o sendvicu imamo:
[latex]a_n:=0 \forall n \in N \\
b_n:=|x`_{p_n}-c|\\
c_n:=|x``_{p_n}-x`_{p_n}|+|x`_{p_n}-c|\\
~ t.d. ~ a_n \leq b_n \leq c_n~ ~\forall n \in N \Longrightarrow 0 = \lim_{n \in N} a_n \leq \lim_{n \in N} b_n \leq \lim_{n \in N} c_n = 0[/latex]
Eto :)
[quote="Vincent Van Ear"]Kada uopće limes smije ''napadati'' jednadžbe[/quote]
Samo kada si u stanju napraviti rezoniranje kao na gornjem "primjeru". Pogledaj u udjbeniku iz MA1 (ili biljeskama) propoziciju o svojstvima limesa nizova (suma, produkt, kvocijent, sendvic itd. - _dobro_ promotri sto su pretpostavke a sto zakljucci teorema). Tu je i "komutativnost" limesa i neprekidne fje iz MA1 i to je... vise manje to?
PS posebno promotri liniju oznacenu sa (!). Cinjenica da je taj limes jednak 0, govori eksplicitno da on i postoji i da je realan (iz |R) :) Jedna je od najcescih pogreski studenata 1. godine prilikom primijene tih teorema jest da zaboravljaju da limesi nizova(a vrijedi i za fje) moraju biti konvergentni da bi limes njihove sume bio konvergentan (tj. da bi limes _postojao_, npr. beskonacnost nije realan broj). OBRAT NE VRIJEDI.
Ako imas limes koji konvergira kojeg mozes raspisati npr. u sumu onda "elementi" te sume ne moraju biti konvergentni, ili na primjeru:
[latex]\lim_{n \in N}[(-1)^n+(-1)^{n+1}]=0[/latex], iako limes niza (-1)^n ne postoji (a time i (-1)^n+1 ;))
| Vincent Van Ear (napisa): | Hm,znaš što me buni,imam x',x'' i c i sada njih počinjem ''slagati'' u nejednakost trokuta,kako ih slažem,kako zaključujem da će mi modul |x''_p_n| biti slijeva,a suma modula |x''_p_n – x'_p_n| i |x'_p_n –c | zdesna?
Što me vodi u toj ''igri slaganja'' da ne griješim gdje ću koji modul staviti s obzirom na nejednakost ?
Vidim tu relaciju i jasno mi je koje informacije mi ''odašilje'' ali zanima me kako je ta relacija ''sklepana'',kako su moduli našli svoje mjesto u njoj? |
Pa.. Zelis dokazati da "podnizi" (ne da mi se pisat indekse) od x' i x'' teze ka istoj vrijednosti (to sto oni samo po sebi teze jedan drugom ti za sada ne govori mnogo i o njihovim fjskim vrijednostima, tu ulazi relacija trokuta). Nasao si da x' ima podniz koji konvergira i rekao da je taj limes=c. Da bi dokazao uniformnu neprekidnost, tj. u nasem slucaju, kontradikciju, moras dokazati da x'' (a dakle i njegove funkcijske vrijednosti) isto teze ka c (tj, f(c), tj. f(x') i f(x'') imaju isti limes).
Sta imamo?
(1) znamo udaljenost od x'' do x'
(2) znamo i udaljenost od x' do c
(3) ono sto ne znamo je udaljenost x'' do c (da mozemo primijeniti onu propoziciju o limesu neprekidne fje), sto je, vidi s(p)retnog cuda  kraca udaljenost od te kada bi npr. isli od x'' do c preko neke trece tocke, npr. x' kraca udaljenost od te kada bi npr. isli od x'' do c preko neke trece tocke, npr. x' 
I sada drugi dio:
| Vincent Van Ear (napisa): | I još nešto starijega :
ti si ovaj izraz:
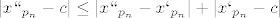
pretvorio u ovaj:
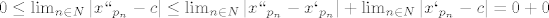
Kako ja tu radnju precizno interpretiram,sigurno ne ukoliko kažem:
djelujemo limesom na relaciju(tako izgleda)? |
Formalno: imamo nejednakost:
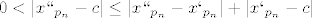
prvo cu promotrit desni dio nejednakosti, tu je stvar dosta cista (x' po definiciji tezi u c a udaljenost od x' do x'' je manja od 1/n tako da:
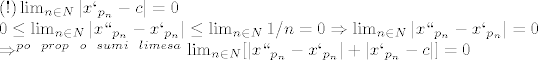
Dakle, opet, primijenom tm. o sendvicu imamo:
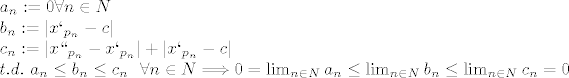
Eto 
| Vincent Van Ear (napisa): | | Kada uopće limes smije ''napadati'' jednadžbe |
Samo kada si u stanju napraviti rezoniranje kao na gornjem "primjeru". Pogledaj u udjbeniku iz MA1 (ili biljeskama) propoziciju o svojstvima limesa nizova (suma, produkt, kvocijent, sendvic itd. - _dobro_ promotri sto su pretpostavke a sto zakljucci teorema). Tu je i "komutativnost" limesa i neprekidne fje iz MA1 i to je... vise manje to?
PS posebno promotri liniju oznacenu sa (!). Cinjenica da je taj limes jednak 0, govori eksplicitno da on i postoji i da je realan (iz |R)  Jedna je od najcescih pogreski studenata 1. godine prilikom primijene tih teorema jest da zaboravljaju da limesi nizova(a vrijedi i za fje) moraju biti konvergentni da bi limes njihove sume bio konvergentan (tj. da bi limes _postojao_, npr. beskonacnost nije realan broj). OBRAT NE VRIJEDI. Jedna je od najcescih pogreski studenata 1. godine prilikom primijene tih teorema jest da zaboravljaju da limesi nizova(a vrijedi i za fje) moraju biti konvergentni da bi limes njihove sume bio konvergentan (tj. da bi limes _postojao_, npr. beskonacnost nije realan broj). OBRAT NE VRIJEDI.
Ako imas limes koji konvergira kojeg mozes raspisati npr. u sumu onda "elementi" te sume ne moraju biti konvergentni, ili na primjeru:
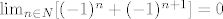 , iako limes niza (-1)^n ne postoji (a time i (-1)^n+1 , iako limes niza (-1)^n ne postoji (a time i (-1)^n+1  ) )
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 11:35 ned, 22. 8. 2004 Naslov: Postano: 11:35 ned, 22. 8. 2004 Naslov: |
    |
|
|
Intuitivno:
-udaljenost između članova nizova x' i x'' za n->oo je sve manja i manja (argument: |x'-x''|<1/n za n@IN)
-onda i udaljenost između članova podnizova mora biti sve manja i manja za n->oo (argument:iz definicije podniza, jer se članovi podniza biraju iz članova niza _uz uvjet_ da se članovi podniza ne biraju nasumice već po pravilu-ako sam uzeo za prvi član podniza 27. član niza,onda sljedeći član podniza može biti ''najranije'' 28. član niza…)
-ti nizovi imaju konvergentne podnizove (argument:B-W za nizove)
-kako ti podnizovi konvergiraju morati ''ići'' u isti broj (argument:nepoznat,intuitivno-jasno)
[quote]Nasao si da x' ima podniz koji konvergira i rekao da je taj limes=c. Da bi dokazao uniformnu neprekidnost, tj. u nasem slucaju, kontradikciju, moras dokazati da x'' (a dakle i njegove funkcijske vrijednosti) isto teze ka c (tj, f(c), tj. f(x') i f(x'') imaju isti limes).[/quote]
da se to mora dokazati to se lijepo vidi iz _dokaza u cijelosti_.Želim reći,primjerice,nalaziš se na nekoj ''simboličkoj liniji'' dokaza(simbolički tekst do kojeg si kroz dokazivanje došao) i argument zašto naredna linija koju promatraš ''izgleda'' baš tako kako izgleda možeš(ukoliko ti odmah nije jasno) dobiti tako što škicneš malko unaprijed kroz dokaz.
Možda me nečeš shvatiti … :shock:
[quote](1) znamo udaljenost od x'' do x'[/quote]
iz ovoga:
|x'-x''|<1/n
a zapravo iz toga imam i ovu koja me zapravo zanima :
|x'_p_n-x''_p_n|<1/n
[quote](2) znamo i udaljenost od x' do c[/quote]
dali ja stvarno znam udaljenost niza x' od c ?
jesi li možda mislio na udaljenost _podniza niza_ x' od c jer nju imam iz ovoga :
podniz niza x' ima limes u c
[quote]Jedna je od najcescih pogreski studenata 1. godine prilikom primijene tih teorema jest da zaboravljaju da limesi nizova(a vrijedi i za fje) moraju biti konvergentni da bi limes njihove sume bio konvergentan (tj. da bi limes _postojao_, npr. beskonacnost nije realan broj). OBRAT NE VRIJEDI.[/quote]
Istinito,istinito.
Hvala na primjeru.
PS:hej,zakaj nemrem kvotat formule?[/quote]
Intuitivno:
-udaljenost između članova nizova x' i x'' za n→oo je sve manja i manja (argument: |x'-x''|<1/n za n@IN)
-onda i udaljenost između članova podnizova mora biti sve manja i manja za n→oo (argument:iz definicije podniza, jer se članovi podniza biraju iz članova niza _uz uvjet_ da se članovi podniza ne biraju nasumice već po pravilu-ako sam uzeo za prvi član podniza 27. član niza,onda sljedeći član podniza može biti ''najranije'' 28. član niza…)
-ti nizovi imaju konvergentne podnizove (argument:B-W za nizove)
-kako ti podnizovi konvergiraju morati ''ići'' u isti broj (argument:nepoznat,intuitivno-jasno)
| Citat: | | Nasao si da x' ima podniz koji konvergira i rekao da je taj limes=c. Da bi dokazao uniformnu neprekidnost, tj. u nasem slucaju, kontradikciju, moras dokazati da x'' (a dakle i njegove funkcijske vrijednosti) isto teze ka c (tj, f(c), tj. f(x') i f(x'') imaju isti limes). |
da se to mora dokazati to se lijepo vidi iz _dokaza u cijelosti_.Želim reći,primjerice,nalaziš se na nekoj ''simboličkoj liniji'' dokaza(simbolički tekst do kojeg si kroz dokazivanje došao) i argument zašto naredna linija koju promatraš ''izgleda'' baš tako kako izgleda možeš(ukoliko ti odmah nije jasno) dobiti tako što škicneš malko unaprijed kroz dokaz.
Možda me nečeš shvatiti … 
| Citat: | | (1) znamo udaljenost od x'' do x' |
iz ovoga:
|x'-x''|<1/n
a zapravo iz toga imam i ovu koja me zapravo zanima :
|x'_p_n-x''_p_n|<1/n
| Citat: | | (2) znamo i udaljenost od x' do c |
dali ja stvarno znam udaljenost niza x' od c ?
jesi li možda mislio na udaljenost _podniza niza_ x' od c jer nju imam iz ovoga :
podniz niza x' ima limes u c
| Citat: | | Jedna je od najcescih pogreski studenata 1. godine prilikom primijene tih teorema jest da zaboravljaju da limesi nizova(a vrijedi i za fje) moraju biti konvergentni da bi limes njihove sume bio konvergentan (tj. da bi limes _postojao_, npr. beskonacnost nije realan broj). OBRAT NE VRIJEDI. |
Istinito,istinito.
Hvala na primjeru.
PS:hej,zakaj nemrem kvotat formule?[/quote]
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 12:55 ned, 22. 8. 2004 Naslov: Postano: 12:55 ned, 22. 8. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"]Intuitivno:
-udaljenost između članova nizova x' i x'' za n->oo je sve manja i manja (argument: |x'-x''|<1/n za n@IN)
-onda i udaljenost između članova podnizova mora biti sve manja i manja za n->oo (argument:iz definicije podniza, jer se članovi podniza biraju iz članova niza _uz uvjet_ da se članovi podniza ne biraju nasumice već po pravilu-ako sam uzeo za prvi član podniza 27. član niza,onda sljedeći član podniza može biti ''najranije'' 28. član niza…)
-ti nizovi imaju konvergentne podnizove (argument:B-W za nizove)
-kako ti podnizovi konvergiraju morati ''ići'' u isti broj (argument:nepoznat,intuitivno-jasno)[/quote]
_ne moraju_ ;) To smo dokazali kroz relaciju trokuta. Velika nejednakost za intuitivno jasnu stvar, ali tako se radi :)
[quote="Vincent Van Ear"]da se to mora dokazati to se lijepo vidi iz _dokaza u cijelosti_.Želim reći,primjerice,nalaziš se na nekoj ''simboličkoj liniji'' dokaza(simbolički tekst do kojeg si kroz dokazivanje došao) i argument zašto naredna linija koju promatraš ''izgleda'' baš tako kako izgleda možeš(ukoliko ti odmah nije jasno) dobiti tako što škicneš malko unaprijed kroz dokaz.
Možda me nečeš shvatiti … :shock: [/quote]
Donekle shvacam ;) Ako nemas pribliznu ideju, mutnu sliku, o ukupnoj formi dokaza (iliti dokaza u cijelosti), onda si u nevolji (no to je vise stvar inspiracije nego iceg drugog).
Ako znas sto zelis i ako znas sto znas onda nije veliki intelektualni skok primijeniti nejednakost trokuta na onaj nacin..
Iako, moram priznati, neke stvari postanu malo jasnije kada se primijenjuju na 2 i vise dimenzionalnim metr. prostorima. Neke stvari su npr. u ravnini mnogo ocitije nego "na pravcu" :? al naucit ces :)
[quote="Vincent Van Ear"][quote](1) znamo udaljenost od x'' do x'[/quote]
iz ovoga:
|x'-x''|<1/n
a zapravo iz toga imam i ovu koja me zapravo zanima :
|x'_p_n-x''_p_n|<1/n[/quote]
tocno
[quote="Vincent Van Ear"][quote](2) znamo i udaljenost od x' do c[/quote]
dali ja stvarno znam udaljenost niza x' od c ?
jesi li možda mislio na udaljenost _podniza niza_ x' od c jer nju imam iz ovoga :
podniz niza x' ima limes u c[/quote]
Da, na njega sam mislio :) (nije mi se dalo pisati indekse u proslom postu (pa sam to i napomenuo ;)) jer smo samo o tim podnizima i raspravljali)
[quote="Vincent Van Ear"]PS:hej,zakaj nemrem kvotat formule?[/quote]
:blueshock: Beats me :-s
pitaj vsegu :-s, al najprije prouci obavjest pod "Obvezatno stivo", da ne cinis stogod krivo iako mi ne pada napamet sto :-s
| Vincent Van Ear (napisa): | Intuitivno:
-udaljenost između članova nizova x' i x'' za n→oo je sve manja i manja (argument: |x'-x''|<1/n za n@IN)
-onda i udaljenost između članova podnizova mora biti sve manja i manja za n→oo (argument:iz definicije podniza, jer se članovi podniza biraju iz članova niza _uz uvjet_ da se članovi podniza ne biraju nasumice već po pravilu-ako sam uzeo za prvi član podniza 27. član niza,onda sljedeći član podniza može biti ''najranije'' 28. član niza…)
-ti nizovi imaju konvergentne podnizove (argument:B-W za nizove)
-kako ti podnizovi konvergiraju morati ''ići'' u isti broj (argument:nepoznat,intuitivno-jasno) |
_ne moraju_  To smo dokazali kroz relaciju trokuta. Velika nejednakost za intuitivno jasnu stvar, ali tako se radi To smo dokazali kroz relaciju trokuta. Velika nejednakost za intuitivno jasnu stvar, ali tako se radi 
| Vincent Van Ear (napisa): | da se to mora dokazati to se lijepo vidi iz _dokaza u cijelosti_.Želim reći,primjerice,nalaziš se na nekoj ''simboličkoj liniji'' dokaza(simbolički tekst do kojeg si kroz dokazivanje došao) i argument zašto naredna linija koju promatraš ''izgleda'' baš tako kako izgleda možeš(ukoliko ti odmah nije jasno) dobiti tako što škicneš malko unaprijed kroz dokaz.
Možda me nečeš shvatiti …  |
Donekle shvacam  Ako nemas pribliznu ideju, mutnu sliku, o ukupnoj formi dokaza (iliti dokaza u cijelosti), onda si u nevolji (no to je vise stvar inspiracije nego iceg drugog). Ako nemas pribliznu ideju, mutnu sliku, o ukupnoj formi dokaza (iliti dokaza u cijelosti), onda si u nevolji (no to je vise stvar inspiracije nego iceg drugog).
Ako znas sto zelis i ako znas sto znas onda nije veliki intelektualni skok primijeniti nejednakost trokuta na onaj nacin..
Iako, moram priznati, neke stvari postanu malo jasnije kada se primijenjuju na 2 i vise dimenzionalnim metr. prostorima. Neke stvari su npr. u ravnini mnogo ocitije nego "na pravcu"  al naucit ces al naucit ces 
| Vincent Van Ear (napisa): | | Citat: | | (1) znamo udaljenost od x'' do x' |
iz ovoga:
|x'-x''|<1/n
a zapravo iz toga imam i ovu koja me zapravo zanima :
|x'_p_n-x''_p_n|<1/n |
tocno
| Vincent Van Ear (napisa): | | Citat: | | (2) znamo i udaljenost od x' do c |
dali ja stvarno znam udaljenost niza x' od c ?
jesi li možda mislio na udaljenost _podniza niza_ x' od c jer nju imam iz ovoga :
podniz niza x' ima limes u c |
Da, na njega sam mislio  (nije mi se dalo pisati indekse u proslom postu (pa sam to i napomenuo (nije mi se dalo pisati indekse u proslom postu (pa sam to i napomenuo  ) jer smo samo o tim podnizima i raspravljali) ) jer smo samo o tim podnizima i raspravljali)
| Vincent Van Ear (napisa): | | PS:hej,zakaj nemrem kvotat formule? |
 Beats me Beats me 
pitaj vsegu  , al najprije prouci obavjest pod "Obvezatno stivo", da ne cinis stogod krivo iako mi ne pada napamet sto , al najprije prouci obavjest pod "Obvezatno stivo", da ne cinis stogod krivo iako mi ne pada napamet sto 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 14:37 ned, 22. 8. 2004 Naslov: Postano: 14:37 ned, 22. 8. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"][quote]_ne moraju_ [/quote]
I must keep reminding my self of this,ništa se ne mora,osim umrijeti though. :) [/quote]
:pavati:
To jos nije dokazano, iako je cesto zabiljezeno :g:
[quote="Vincent Van Ear"][quote]Ako znas sto zelis i ako znas sto znas onda nije veliki intelektualni skok primijeniti nejednakost trokuta na onaj nacin..[/quote]
E sad zeleni…o visini ograde za skok bi mogli raspravljati jeli?!
:D [/quote]
:shrug: to je tehnicka stvar, a tehnicke stvari su stvar vjezbe ;) pozdrav
| Vincent Van Ear (napisa): |
I must keep reminding my self of this,ništa se ne mora,osim umrijeti though.  |

To jos nije dokazano, iako je cesto zabiljezeno 
| Vincent Van Ear (napisa): | | Citat: | | Ako znas sto zelis i ako znas sto znas onda nije veliki intelektualni skok primijeniti nejednakost trokuta na onaj nacin.. |
E sad zeleni…o visini ograde za skok bi mogli raspravljati jeli?!
 |
:shrug: to je tehnicka stvar, a tehnicke stvari su stvar vjezbe  pozdrav pozdrav
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 10:08 pon, 23. 8. 2004 Naslov: Postano: 10:08 pon, 23. 8. 2004 Naslov: |
    |
|
|
[quote]Mozebit da sam ja pobrkao loncice, al, ako nejednakost trokuta odozgora "nahranimo" u teorem o sendvicu onda cemo imati:
Ah gle to si i ti napisao Ok, prvi sumand ide u 0 jer smo ga tako definirali, drugi smo sad obrazlozili[/quote]
sorry što povlačim stare stvari ali ova ''pohrana'' u sendvič bi išla ovako? :
(a_n)=0 on je konvergentan(jer je stacionaran niz)
(b_n)=|x''_p_n-c|
(c_n)=|x''_p_n-x'_p_n|+|x'_p_n-c| on je konvergentan
Sve je legitimno,(a_n) je ''stvoren'' da bude ''donja kriška sendviča'',a naravno i sasvim je legitimno za zaključiti da je udaljenost dva broja strogo veća ili jednaka nuli, pa imamo da vrijedi odnos :
0<=|x''_p_n-c|<=| x''_p_n-x'_p_n|+|x'_p_n-c|
Iz takvih činjenica imamo doprinos teorema o sendviču => niz (|x''_p_n-c|) je konvergentan i limes mu je jednak limesu od (a_n) i (b_n).
Odnosno kriška salame mora biti nužno uklještena između šnita kruha i ona baš kao i šnite neće izbjeći proždiranje pohlapljivih usta.
:wink:
| Citat: | Mozebit da sam ja pobrkao loncice, al, ako nejednakost trokuta odozgora "nahranimo" u teorem o sendvicu onda cemo imati:
Ah gle to si i ti napisao Ok, prvi sumand ide u 0 jer smo ga tako definirali, drugi smo sad obrazlozili |
sorry što povlačim stare stvari ali ova ''pohrana'' u sendvič bi išla ovako? :
(a_n)=0 on je konvergentan(jer je stacionaran niz)
(b_n)=|x''_p_n-c|
(c_n)=|x''_p_n-x'_p_n|+|x'_p_n-c| on je konvergentan
Sve je legitimno,(a_n) je ''stvoren'' da bude ''donja kriška sendviča'',a naravno i sasvim je legitimno za zaključiti da je udaljenost dva broja strogo veća ili jednaka nuli, pa imamo da vrijedi odnos :
0⇐|x''_p_n-c|⇐| x''_p_n-x'_p_n|+|x'_p_n-c|
Iz takvih činjenica imamo doprinos teorema o sendviču ⇒ niz (|x''_p_n-c|) je konvergentan i limes mu je jednak limesu od (a_n) i (b_n).
Odnosno kriška salame mora biti nužno uklještena između šnita kruha i ona baš kao i šnite neće izbjeći proždiranje pohlapljivih usta.

_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 10:58 pon, 23. 8. 2004 Naslov: Postano: 10:58 pon, 23. 8. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"]sorry što povlačim stare stvari ali ova ''pohrana'' u sendvič bi išla ovako? :
(a_n)=0 on je konvergentan(jer je stacionaran niz)
......
Odnosno kriška salame mora biti nužno uklještena između šnita kruha i ona baš kao i šnite neće izbjeći proždiranje pohlapljivih usta.
:wink:[/quote]
:klopa: potpuno u pravu :g:
| Vincent Van Ear (napisa): | sorry što povlačim stare stvari ali ova ''pohrana'' u sendvič bi išla ovako? :
(a_n)=0 on je konvergentan(jer je stacionaran niz)
......
Odnosno kriška salame mora biti nužno uklještena između šnita kruha i ona baš kao i šnite neće izbjeći proždiranje pohlapljivih usta.
 |
 potpuno u pravu potpuno u pravu 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 14:14 pon, 23. 8. 2004 Naslov: Postano: 14:14 pon, 23. 8. 2004 Naslov: |
    |
|
|
Evo da onda još jednu sitnicu ovdje izložim,ne primarno vezanu za temu ali ipak kompatibilnu :) jer se tiče limesa(zeleni ih nije volio :D ):
Da ne iznosim jedan teorem u vezi integrala u cijelosti dat ću komad iz kojega je jasno što me zanima(ukoliko bude potrebno podastrijet ću cijeli dokaz,ali mislim da to neće biti nužno;))
Imate F : I -> IR ,I-podskup skupa IR,F neprekidna,funkcija f se definira na isti način.
Nadalje :
c@I te v@<c,x>
Imam relaciju :
F(x)-F(c)/x-c = f(v) (*)
Kaže se :postoji limes lim_{x->c} F(x)-F(c)/x-c=f(c)
Iz čega je to zaključeno ?
Ja bih (dakako)neprecizno rekao :
Na relaciju zvjezdica je primijenjen limes kada ide x prema c(mene zanima kada se na funkcije smije primjenjivati limes,pod kojim uvjetima?),naravno da i v ide prema c jer je v upravo iz toga okruženja pa je limes zdesne strane =f(c) dakle konkretnoj fiksnoj vrijednosti iz čega se zaključuje(jednakost ne laže) da je tome jednak limes slijeve strane.
Nije mi bitna intencija zbog koje ispitujemo limes jer mi je ona u potpunosti jasna.
Evo da onda još jednu sitnicu ovdje izložim,ne primarno vezanu za temu ali ipak kompatibilnu  jer se tiče limesa(zeleni ih nije volio jer se tiče limesa(zeleni ih nije volio  ): ):
Da ne iznosim jedan teorem u vezi integrala u cijelosti dat ću komad iz kojega je jasno što me zanima(ukoliko bude potrebno podastrijet ću cijeli dokaz,ali mislim da to neće biti nužno;))
Imate F : I -> IR ,I-podskup skupa IR,F neprekidna,funkcija f se definira na isti način.
Nadalje :
c@I te v@<c,x>
Imam relaciju :
F(x)-F(c)/x-c = f(v) (*)
Kaže se :postoji limes lim_{x->c} F(x)-F(c)/x-c=f(c)
Iz čega je to zaključeno ?
Ja bih (dakako)neprecizno rekao :
Na relaciju zvjezdica je primijenjen limes kada ide x prema c(mene zanima kada se na funkcije smije primjenjivati limes,pod kojim uvjetima?),naravno da i v ide prema c jer je v upravo iz toga okruženja pa je limes zdesne strane =f(c) dakle konkretnoj fiksnoj vrijednosti iz čega se zaključuje(jednakost ne laže) da je tome jednak limes slijeve strane.
Nije mi bitna intencija zbog koje ispitujemo limes jer mi je ona u potpunosti jasna.
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 16:29 uto, 24. 8. 2004 Naslov: Postano: 16:29 uto, 24. 8. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"]Evo da onda još jednu sitnicu ovdje izložim,ne primarno vezanu za temu ali ipak kompatibilnu :) jer se tiče limesa(zeleni ih nije volio :D ):[/quote]
Nenene, teorija je lijepa, ono sto mi je ruzno jest primijena te teorije "na ruke" na probleme za koje u normalnim slucajevima postoji Mathematica, a ako ne vec ona, onda barem svijest o liku i dijelu mr. L'Hospitala :g:
[quote="Vincent Van Ear"]Imate F : I -> IR ,I-podskup skupa IR,F neprekidna,funkcija f se definira na isti način.
Nadalje :
c@I te v@<c,x>
Imam relaciju :
F(x)-F(c)/x-c = f(v) (*)[/quote]
Ovako.. f(v) jest neprekidna fja u c, dakle: njen limes kada x tezi u c je jednak f(c). To trenutacno cak i nije toliko vazan podatak koliko da taj limes _POSTOJI_. Dakle postoji takav L iz |R t.d. (u epsilon/delta jeziku):
[latex]~(L) ~(\forall \varepsilon > 0) (\exists \delta_L > 0) ~ t.d. ~ |x-c|<\delta_L \Rightarrow \left|\frac{F(x)-F(c)}{x-c} - L\right| < \varepsilon \\
~(D) ~(\forall \varepsilon > 0) (\exists \delta_D > 0) ~ t.d. ~ |v-c|<\delta_D \Rightarrow |f(v)-L| < \varepsilon \Rightarrow \\
~def. ~ \delta:=\min\{\delta_L, \delta_D\} \\
(\forall \varepsilon > 0) (\exists \delta > 0) ~ t.d. ~ |x-c|<\delta \Rightarrow \left|\frac{F(x)-F(c)}{x-c} - L \right| < \varepsilon ~ i ~ |f(x)-L| < \varepsilon \Rightarrow\\
\lim_{x \rightarrow c} \frac{F(x)-F(c)}{x-c} = L = \lim_{x \rightarrow c} f(x) = ~ :) ~ f(c)[/latex]
[quote="Vincent Van Ear"]Kaže se :postoji limes lim_{x->c} F(x)-F(c)/x-c=f(c)[/quote]
Da :) na nasu srecu taj limes je jednak f(c) pa to mozemo tako lijepo reci :)
[quote="Vincent Van Ear"]Iz čega je to zaključeno ?[/quote]
vidi gore ;)
tako bi se to moglo formalno opravdati, al rezultat je bio jasan i prije nego smo to formalno izrazili tako da vjerujem da bi te malo tko pitao da mu to i dokazes, iako, narafski, od tebe se ocekuje da to _znas_ opravdati ukoliko te itko pita :g:
[quote="Vincent Van Ear"]Ja bih (dakako)neprecizno rekao :
Na relaciju zvjezdica je primijenjen limes kada ide x prema c(mene zanima kada se na funkcije smije primjenjivati limes,pod kojim uvjetima?)[/quote]
"limes se moze primijeniti" skoro uvijek ;) (tj. na sve one fje definirane na nekoj okolini tocke u kojoj taj limes promatramo (ne nuzno i u samoj toj tocki)) pitanje koje ti zelis postaviti jest kada ima smisla promatrati njegovu vrijednost :) naravno, onda kada je ona realna :) tj. kada limes _postoji_. Egzistenciju limesa na desnoj strani relacije nam osigurava ona slavna propozicija o limesu neprekidne fje u tocki, a buduci da je lijeva strana "po tockama" jednaka lijevoj, tada i lijeva strana ima limes, i to limes koji je jednak limesu desnog dijela relacije, dakle, postoji L....... :) (dalje vidi gore)
[quote="Vincent Van Ear"]naravno da i v ide prema c jer je v upravo iz toga okruženja pa je limes zdesne strane =f(c) dakle konkretnoj fiksnoj vrijednosti iz čega se zaključuje(jednakost ne laže) da je tome jednak limes slijeve strane.[/quote]
:shock: suzdrzi se od obrazlozenja poput "jednakost ne laze" :lol: kada izadjes predj djelata na usmeni :) Malo preciznije bi gornji kvout izrazio:
[i]"limes desne strane postoji zbog propozicije o limesu neprekidne fje, a buduci da je lijeva strana po tockama jednaka desnoj, tada je to limes i lijeve strane i taj limes je jednak f(c)"[/i]
I onaj "naravno da i v..." bi mozda prosao na usmenom, ali bi to trebao znati obrazloziti epsilon/delta jezikom ako te itko pita :)
| Vincent Van Ear (napisa): | Evo da onda još jednu sitnicu ovdje izložim,ne primarno vezanu za temu ali ipak kompatibilnu  jer se tiče limesa(zeleni ih nije volio jer se tiče limesa(zeleni ih nije volio  ): ): |
Nenene, teorija je lijepa, ono sto mi je ruzno jest primijena te teorije "na ruke" na probleme za koje u normalnim slucajevima postoji Mathematica, a ako ne vec ona, onda barem svijest o liku i dijelu mr. L'Hospitala 
| Vincent Van Ear (napisa): | Imate F : I → IR ,I-podskup skupa IR,F neprekidna,funkcija f se definira na isti način.
Nadalje :
c@I te v@<c,x>
Imam relaciju :
F(x)-F(c)/x-c = f(v) (*) |
Ovako.. f(v) jest neprekidna fja u c, dakle: njen limes kada x tezi u c je jednak f(c). To trenutacno cak i nije toliko vazan podatak koliko da taj limes _POSTOJI_. Dakle postoji takav L iz |R t.d. (u epsilon/delta jeziku):
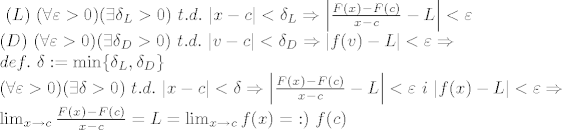
| Vincent Van Ear (napisa): | | Kaže se :postoji limes lim_{x→c} F(x)-F(c)/x-c=f(c) |
Da  na nasu srecu taj limes je jednak f(c) pa to mozemo tako lijepo reci na nasu srecu taj limes je jednak f(c) pa to mozemo tako lijepo reci 
| Vincent Van Ear (napisa): | | Iz čega je to zaključeno ? |
vidi gore 
tako bi se to moglo formalno opravdati, al rezultat je bio jasan i prije nego smo to formalno izrazili tako da vjerujem da bi te malo tko pitao da mu to i dokazes, iako, narafski, od tebe se ocekuje da to _znas_ opravdati ukoliko te itko pita 
| Vincent Van Ear (napisa): | Ja bih (dakako)neprecizno rekao :
Na relaciju zvjezdica je primijenjen limes kada ide x prema c(mene zanima kada se na funkcije smije primjenjivati limes,pod kojim uvjetima?) |
"limes se moze primijeniti" skoro uvijek  (tj. na sve one fje definirane na nekoj okolini tocke u kojoj taj limes promatramo (ne nuzno i u samoj toj tocki)) pitanje koje ti zelis postaviti jest kada ima smisla promatrati njegovu vrijednost (tj. na sve one fje definirane na nekoj okolini tocke u kojoj taj limes promatramo (ne nuzno i u samoj toj tocki)) pitanje koje ti zelis postaviti jest kada ima smisla promatrati njegovu vrijednost  naravno, onda kada je ona realna naravno, onda kada je ona realna  tj. kada limes _postoji_. Egzistenciju limesa na desnoj strani relacije nam osigurava ona slavna propozicija o limesu neprekidne fje u tocki, a buduci da je lijeva strana "po tockama" jednaka lijevoj, tada i lijeva strana ima limes, i to limes koji je jednak limesu desnog dijela relacije, dakle, postoji L....... tj. kada limes _postoji_. Egzistenciju limesa na desnoj strani relacije nam osigurava ona slavna propozicija o limesu neprekidne fje u tocki, a buduci da je lijeva strana "po tockama" jednaka lijevoj, tada i lijeva strana ima limes, i to limes koji je jednak limesu desnog dijela relacije, dakle, postoji L.......  (dalje vidi gore) (dalje vidi gore)
| Vincent Van Ear (napisa): | | naravno da i v ide prema c jer je v upravo iz toga okruženja pa je limes zdesne strane =f(c) dakle konkretnoj fiksnoj vrijednosti iz čega se zaključuje(jednakost ne laže) da je tome jednak limes slijeve strane. |
 suzdrzi se od obrazlozenja poput "jednakost ne laze" suzdrzi se od obrazlozenja poput "jednakost ne laze"  kada izadjes predj djelata na usmeni kada izadjes predj djelata na usmeni  Malo preciznije bi gornji kvout izrazio: Malo preciznije bi gornji kvout izrazio:
"limes desne strane postoji zbog propozicije o limesu neprekidne fje, a buduci da je lijeva strana po tockama jednaka desnoj, tada je to limes i lijeve strane i taj limes je jednak f(c)"
I onaj "naravno da i v..." bi mozda prosao na usmenom, ali bi to trebao znati obrazloziti epsilon/delta jezikom ako te itko pita 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
|




