|
[quote="357951"]odredite parametar @ tako da je
[code:1]
e^-x , x<0
f(x)={
2x-x^2+@, x=>0
[/code:1]
bude neprekinuta na R i za taj @ izracunajte globalne ekstreme funcije f na [-2,3/2].
Zna netko ovo rijesiti, ja stalno zapnem.
P.S.
Moze li detaljno objašnjenje prilikom postupka![/quote]
[latex]lim_{_{x\rightarrow 0}}e^{-x}=1\Longrightarrow @=1[/latex], jer za x=0 u drugom izrazu se treba dobiti 1.
Deriviranjem dobiješ [latex]f^{(1)}(x)=2-2x, x\geq 0 [/latex]
Pa ti nakon izjednačavanja s nulom slijedi:
MAXIMUM=max{f(-2), f(3/2), f(1)}
MINIMUM=min{f(-2), f(3/2), f(1)}
Nadam se da je dovoljno jasno. :)
| 357951 (napisa): | odredite parametar @ tako da je
| Kod: |
e^-x , x<0
f(x)={
2x-x^2+@, x=>0
|
bude neprekinuta na R i za taj @ izracunajte globalne ekstreme funcije f na [-2,3/2].
Zna netko ovo rijesiti, ja stalno zapnem.
P.S.
Moze li detaljno objašnjenje prilikom postupka! |
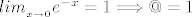 , jer za x=0 u drugom izrazu se treba dobiti 1.
Deriviranjem dobiješ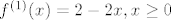 
Pa ti nakon izjednačavanja s nulom slijedi:
MAXIMUM=max{f(-2), f(3/2), f(1)}
MINIMUM=min{f(-2), f(3/2), f(1)}
Nadam se da je dovoljno jasno. 
|
