|
[quote="Tonci"]Imam problema s dokazivanjem da su svaka dva integera usporediva s obzirom na relaciju "biti element". Dokaz bi vjerojatno trebao slijediti iz definicije integera (skup koji je sadrzan u svakom induktivnom skupu), ali mi ne uspijeva dokazati. Ukoliko bi mi netko mogao pomoci, bio bih zahvalan.[/quote]
Indukcija je ključ. Neka su i i j dva prirodna broja. Indukcijom po i , dokažimo da [latex]\forall_i^\omega\forall_j^\omega(i\in j\vee i=j\vee j\in i)[/latex].
[b]Baza:[/b] i=0 . Trebamo dokazati da je za svaki prirodan j , j=0V0@j
(očito j !@ 0 ). To dokazujemo ugniježđenom indukcijom po j .
Za j=0 disjunkcija vrijedi. Pretpostavimo da je za prirodan k , k=0V0@k . Ako je k=0 , tad je k'=1=0'=0U{0}={0} , pa je 0@k' .
Ako je naprotiv 0@k , tad je 0 @ k C= k U {k} = k' , pa je opet 0@k' .
Baza dokazana.
[b]Pretpostavka:[/b] Pretpostavimo da, za prirodan k , za svaki prirodan j vrijedi j=kVj@kVk@j . To će nam u koraku dati dva slučaja koja moramo razmotriti: (a) j=kVj@k , te (b) k@j .
[b]Korak:[/b] Pogledajmo što je s k' . Trebamo dokazati [latex]\forall_j^\omega(j\in k^+\vee j=k^+\vee k^+\in j)[/latex].
U slučaju (a) , imamo j=kVj@k<=>j@{k}Vj@k<=>j@kU{k}=k' , pa je tvrdnja dokazana.
U slučaju (b) , imamo k@j . Dokažimo da to uvijek povlači k'@jVk'=j . To opet ide indukcijom po j .
Ako je j=0 , nema takvih k@j , pa je tvrdnja ispunjena.
Pretpostavimo da za prirodni l , k@l povlači k'@lVk'=l .
Uzmimo proizvoljni m@l' (trebamo dokazati m'@l' ili m'=l' ). To znači m=l ili m@l . Ako je m=l , tad je trivijalno m'=l' ( ' je deterministička: ). Ako je pak m@l , po pretpostavci indukcije je m'@l ili m'=l . Drugi slučaj, m'=l , direktno povlači m'@l' (jer je l@l' ), dok prvi, m'@l , također povlači m'@l' (jer je lCl' ).
[b]QED[/b].
Mislim da nisam ništa zaboravio. :-)
| Tonci (napisa): | | Imam problema s dokazivanjem da su svaka dva integera usporediva s obzirom na relaciju "biti element". Dokaz bi vjerojatno trebao slijediti iz definicije integera (skup koji je sadrzan u svakom induktivnom skupu), ali mi ne uspijeva dokazati. Ukoliko bi mi netko mogao pomoci, bio bih zahvalan. |
Indukcija je ključ. Neka su i i j dva prirodna broja. Indukcijom po i , dokažimo da 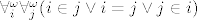 . .
Baza: i=0 . Trebamo dokazati da je za svaki prirodan j , j=0V0@j
(očito j !@ 0 ). To dokazujemo ugniježđenom indukcijom po j .
Za j=0 disjunkcija vrijedi. Pretpostavimo da je za prirodan k , k=0V0@k . Ako je k=0 , tad je k'=1=0'=0U{0}={0} , pa je 0@k' .
Ako je naprotiv 0@k , tad je 0 @ k C= k U {k} = k' , pa je opet 0@k' .
Baza dokazana.
Pretpostavka: Pretpostavimo da, za prirodan k , za svaki prirodan j vrijedi j=kVj@kVk@j . To će nam u koraku dati dva slučaja koja moramo razmotriti: (a) j=kVj@k , te (b) k@j .
Korak: Pogledajmo što je s k' . Trebamo dokazati 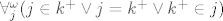 . .
U slučaju (a) , imamo j=kVj@k⇔j@{k}Vj@k⇔j@kU{k}=k' , pa je tvrdnja dokazana.
U slučaju (b) , imamo k@j . Dokažimo da to uvijek povlači k'@jVk'=j . To opet ide indukcijom po j .
Ako je j=0 , nema takvih k@j , pa je tvrdnja ispunjena.
Pretpostavimo da za prirodni l , k@l povlači k'@lVk'=l .
Uzmimo proizvoljni m@l' (trebamo dokazati m'@l' ili m'=l' ). To znači m=l ili m@l . Ako je m=l , tad je trivijalno m'=l' ( ' je deterministička: ). Ako je pak m@l , po pretpostavci indukcije je m'@l ili m'=l . Drugi slučaj, m'=l , direktno povlači m'@l' (jer je l@l' ), dok prvi, m'@l , također povlači m'@l' (jer je lCl' ).
QED.
Mislim da nisam ništa zaboravio. 
|






