| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 19:02 sub, 11. 9. 2004 Naslov: Parcijalno uredjeni skupovi - Dilworthov teorem Postano: 19:02 sub, 11. 9. 2004 Naslov: Parcijalno uredjeni skupovi - Dilworthov teorem |
    |
|
|
DEF. Parcijalno uredjenim skupom zovemo uredjen par [latex](P, \le)[/latex], gdje je [latex]\le[/latex] parcijalni uredjaj na P!=0, tj. binarna relacija koja je refleksivna, antisimetricna i tranzitivna.
DEF. Lanac u [latex](P, \le)[/latex] jest podskup od P u kojem su svaka dva elementa usporediva.
..i sada imamo Dilworthov teorem:
Neka je [latex](P, \le)[/latex] konacan p.u. skup sirine k. Tada postoji particija od P u k lanaca [latex]C_1, ..., C_k[/latex]. Teorem vrijedi i za lokalno konacne p.u. skupove (tj. one ciji je svaki segment konacan skup)
dokaz ide indukcijom po cardP. Za bazu indukcije uzmemo 1, jest, tvrdnja vrijedi, pretpostavljamo da postoji n itd. itd. Ideja dokaza ide od "skracivanja" skupa P (t.d. |P|=n) za minimalni i maksimalni clan koji su usporedivi i tada slijedi 15-ak linija teksta koji mi se cine blago suvisnim za sam dokaz tvrdnje:
moje pitanje, ne bi li doticni teorem bio dokazan i da smo skupu P dodali proizvoljni element x i time dobili skup. npr. P', takav da je |P'|=n+1 sa, opet, proizvoljnim parcijalnim uredjajem i "nahranili" taj novi element u zasebni lanac, npr. [latex]C_{k+1}[/latex] bez obzira na parcijalni uredjaj? (time na trivijalan nacin dobivsi p.u. skup od n+1 elementa u k+1 lanaca?)
napomena: nigdje nije napomenut nikakav uvijet za minimalnost broja lanaca :?
ili prava vaznost teorema lezi u tvrdnji o lokalno konacnim p.u. skupovima koja se u knjizi nalazi u maloj zagradi na kraju iskaza teorema?
...sto opet vodi do iduceg pitanja, a to je, kako je moguce podijeliti skup u konacnu particiju konacnih skupova? :-s
...jer.. ukoliko nije moguce beskonacan skup podijeliti u konacnu particiju konacnih skupova/lanaca, tada gornji dokaz (onaj moj "retardirani") pokriva sve lokalno konacne skupove?
DEF. Parcijalno uredjenim skupom zovemo uredjen par 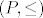 , gdje je , gdje je 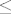 parcijalni uredjaj na P!=0, tj. binarna relacija koja je refleksivna, antisimetricna i tranzitivna. parcijalni uredjaj na P!=0, tj. binarna relacija koja je refleksivna, antisimetricna i tranzitivna.
DEF. Lanac u 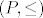 jest podskup od P u kojem su svaka dva elementa usporediva. jest podskup od P u kojem su svaka dva elementa usporediva.
..i sada imamo Dilworthov teorem:
Neka je 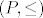 konacan p.u. skup sirine k. Tada postoji particija od P u k lanaca konacan p.u. skup sirine k. Tada postoji particija od P u k lanaca  . Teorem vrijedi i za lokalno konacne p.u. skupove (tj. one ciji je svaki segment konacan skup) . Teorem vrijedi i za lokalno konacne p.u. skupove (tj. one ciji je svaki segment konacan skup)
dokaz ide indukcijom po cardP. Za bazu indukcije uzmemo 1, jest, tvrdnja vrijedi, pretpostavljamo da postoji n itd. itd. Ideja dokaza ide od "skracivanja" skupa P (t.d. |P|=n) za minimalni i maksimalni clan koji su usporedivi i tada slijedi 15-ak linija teksta koji mi se cine blago suvisnim za sam dokaz tvrdnje:
moje pitanje, ne bi li doticni teorem bio dokazan i da smo skupu P dodali proizvoljni element x i time dobili skup. npr. P', takav da je |P'|=n+1 sa, opet, proizvoljnim parcijalnim uredjajem i "nahranili" taj novi element u zasebni lanac, npr. 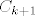 bez obzira na parcijalni uredjaj? (time na trivijalan nacin dobivsi p.u. skup od n+1 elementa u k+1 lanaca?) bez obzira na parcijalni uredjaj? (time na trivijalan nacin dobivsi p.u. skup od n+1 elementa u k+1 lanaca?)
napomena: nigdje nije napomenut nikakav uvijet za minimalnost broja lanaca 
ili prava vaznost teorema lezi u tvrdnji o lokalno konacnim p.u. skupovima koja se u knjizi nalazi u maloj zagradi na kraju iskaza teorema?
...sto opet vodi do iduceg pitanja, a to je, kako je moguce podijeliti skup u konacnu particiju konacnih skupova? 
...jer.. ukoliko nije moguce beskonacan skup podijeliti u konacnu particiju konacnih skupova/lanaca, tada gornji dokaz (onaj moj "retardirani") pokriva sve lokalno konacne skupove?
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 20:07 sub, 11. 9. 2004 Naslov: Re: Parcijalno uredjeni skupovi - Dilworthov teorem Postano: 20:07 sub, 11. 9. 2004 Naslov: Re: Parcijalno uredjeni skupovi - Dilworthov teorem |
    |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"]DEF. Parcijalno uredjenim skupom zovemo uredjen par [latex](P, \le)[/latex], gdje je [latex]\le[/latex] parcijalni uredjaj na P!=0, tj. binarna relacija koja je refleksivna, antisimetricna i tranzitivna.
DEF. Lanac u [latex](P, \le)[/latex] jest podskup od P u kojem su svaka dva elementa usporediva.
..i sada imamo Dilworthov teorem:
Neka je [latex](P, \le)[/latex] konacan p.u. skup sirine k.[/quote]
Nisi definirao što je širina, no pretpostavit ću da je to duljina najduljeg antilanca.
[quote] Tada postoji particija od P u k lanaca [latex]C_1, ..., C_k[/latex]. Teorem vrijedi i za lokalno konacne p.u. skupove (tj. one ciji je svaki segment konacan skup)
dokaz ide indukcijom po cardP. Za bazu indukcije uzmemo 1, jest, tvrdnja vrijedi, pretpostavljamo da postoji n itd. itd. Ideja dokaza ide od "skracivanja" skupa P (t.d. |P|=n) za minimalni i maksimalni clan koji su usporedivi i tada slijedi 15-ak linija teksta koji mi se cine blago suvisnim za sam dokaz tvrdnje:[/quote]
A čuj, tak je to obično u teoriji skupova, grani matha koja bez problema dokazuje da je 2+2=4 i slične stvari... ;-)
[quote]moje pitanje, ne bi li doticni teorem bio dokazan i da smo skupu P dodali proizvoljni element x i time dobili skup. npr. P', takav da je |P'|=n+1 sa, opet, proizvoljnim parcijalnim uredjajem i "nahranili" taj novi element u zasebni lanac, npr. [latex]C_{k+1}[/latex] bez obzira na parcijalni uredjaj? (time na trivijalan nacin dobivsi p.u. skup od n+1 elementa u k+1 lanaca?)[/quote]
Naravno da ne. Ti imaš u pretpostavci teorema već zadan poset (P,<=) , _čija je širina_ k _već određena_. I ti moraš _toliko_ lanaca proizvesti - ne (nužno) onoliko koliko si imao u pretpostavci indukcije, plus jedan.
Ukoliko bi se dodavanjem novog elementa u poset širina uvijek povećavala za jedan (ie, on bi uvijek bio neusporediv sa svima ostalima), tvoj "dokaz" bi prošao. No naravno, to je, blago rečeno, prejaka pretpostavka. (Grubo rečeno, to je glupost.: )
[quote]napomena: nigdje nije napomenut nikakav uvijet za minimalnost broja lanaca :?[/quote]
Hm:?: "Particija u k lanaca" je upravo to, particija. Svaki element mora biti u točno jednom lancu, lanci moraju biti neprazni, i mora ih biti točno k . Tu ništa nisu gornje ili donje ograde, već konkretni iznosi. Ne kužim što ti je "minimalnost broja lanaca".
[quote]ili prava vaznost teorema lezi u tvrdnji o lokalno konacnim p.u. skupovima koja se u knjizi nalazi u maloj zagradi na kraju iskaza teorema?[/quote]
Ako te veseli... :-)
Još uvijek ima ljudî koji tvrde da je matematika znanost o beskonačnom, i da je konačno uvijek trivijalno. Takvi očito nisu vidjeli Ramseyevu teoriju... :shock: ;-)
[quote]...sto opet vodi do iduceg pitanja, a to je, kako je moguce podijeliti skup u konacnu particiju konacnih skupova? :-s[/quote]
Otkud ti pak takva ideja sad?
_segmenti_ su konačni (u lofi-posetu). _lanci_, naravno, ne moraju biti.
Evo ti trivijalni primjer: |Z . Standardni uređaj. toset . Širina 1 (svi su usporedivi). Naravno, cijeli je jedan lanac. Beskonačan, ofcourse.
Ali je lokalno konačan. Između svaka dva cijela broja ima konačno mnogo cijelih brojeva.
[quote]...jer.. ukoliko nije moguce beskonacan skup podijeliti u konacnu particiju konacnih skupova/lanaca, tada gornji dokaz (onaj moj "retardirani") pokriva sve lokalno konacne skupove?[/quote]
Nadam se da je sad jasnije.
| ZELENIZUBNAPLANETIDOSADE (napisa): | DEF. Parcijalno uredjenim skupom zovemo uredjen par 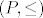 , gdje je , gdje je 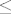 parcijalni uredjaj na P!=0, tj. binarna relacija koja je refleksivna, antisimetricna i tranzitivna. parcijalni uredjaj na P!=0, tj. binarna relacija koja je refleksivna, antisimetricna i tranzitivna.
DEF. Lanac u 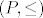 jest podskup od P u kojem su svaka dva elementa usporediva. jest podskup od P u kojem su svaka dva elementa usporediva.
..i sada imamo Dilworthov teorem:
Neka je 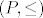 konacan p.u. skup sirine k. konacan p.u. skup sirine k. |
Nisi definirao što je širina, no pretpostavit ću da je to duljina najduljeg antilanca.
| Citat: | Tada postoji particija od P u k lanaca  . Teorem vrijedi i za lokalno konacne p.u. skupove (tj. one ciji je svaki segment konacan skup) . Teorem vrijedi i za lokalno konacne p.u. skupove (tj. one ciji je svaki segment konacan skup)
dokaz ide indukcijom po cardP. Za bazu indukcije uzmemo 1, jest, tvrdnja vrijedi, pretpostavljamo da postoji n itd. itd. Ideja dokaza ide od "skracivanja" skupa P (t.d. |P|=n) za minimalni i maksimalni clan koji su usporedivi i tada slijedi 15-ak linija teksta koji mi se cine blago suvisnim za sam dokaz tvrdnje: |
A čuj, tak je to obično u teoriji skupova, grani matha koja bez problema dokazuje da je 2+2=4 i slične stvari... 
| Citat: | moje pitanje, ne bi li doticni teorem bio dokazan i da smo skupu P dodali proizvoljni element x i time dobili skup. npr. P', takav da je |P'|=n+1 sa, opet, proizvoljnim parcijalnim uredjajem i "nahranili" taj novi element u zasebni lanac, npr. 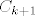 bez obzira na parcijalni uredjaj? (time na trivijalan nacin dobivsi p.u. skup od n+1 elementa u k+1 lanaca?) bez obzira na parcijalni uredjaj? (time na trivijalan nacin dobivsi p.u. skup od n+1 elementa u k+1 lanaca?) |
Naravno da ne. Ti imaš u pretpostavci teorema već zadan poset (P,⇐) , _čija je širina_ k _već određena_. I ti moraš _toliko_ lanaca proizvesti - ne (nužno) onoliko koliko si imao u pretpostavci indukcije, plus jedan.
Ukoliko bi se dodavanjem novog elementa u poset širina uvijek povećavala za jedan (ie, on bi uvijek bio neusporediv sa svima ostalima), tvoj "dokaz" bi prošao. No naravno, to je, blago rečeno, prejaka pretpostavka. (Grubo rečeno, to je glupost.: )
| Citat: | napomena: nigdje nije napomenut nikakav uvijet za minimalnost broja lanaca  |
Hm:?: "Particija u k lanaca" je upravo to, particija. Svaki element mora biti u točno jednom lancu, lanci moraju biti neprazni, i mora ih biti točno k . Tu ništa nisu gornje ili donje ograde, već konkretni iznosi. Ne kužim što ti je "minimalnost broja lanaca".
| Citat: | | ili prava vaznost teorema lezi u tvrdnji o lokalno konacnim p.u. skupovima koja se u knjizi nalazi u maloj zagradi na kraju iskaza teorema? |
Ako te veseli... 
Još uvijek ima ljudî koji tvrde da je matematika znanost o beskonačnom, i da je konačno uvijek trivijalno. Takvi očito nisu vidjeli Ramseyevu teoriju...  
| Citat: | ...sto opet vodi do iduceg pitanja, a to je, kako je moguce podijeliti skup u konacnu particiju konacnih skupova?  |
Otkud ti pak takva ideja sad?
_segmenti_ su konačni (u lofi-posetu). _lanci_, naravno, ne moraju biti.
Evo ti trivijalni primjer: |Z . Standardni uređaj. toset . Širina 1 (svi su usporedivi). Naravno, cijeli je jedan lanac. Beskonačan, ofcourse.
Ali je lokalno konačan. Između svaka dva cijela broja ima konačno mnogo cijelih brojeva.
| Citat: | | ...jer.. ukoliko nije moguce beskonacan skup podijeliti u konacnu particiju konacnih skupova/lanaca, tada gornji dokaz (onaj moj "retardirani") pokriva sve lokalno konacne skupove? |
Nadam se da je sad jasnije.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 20:32 sub, 11. 9. 2004 Naslov: Re: Parcijalno uredjeni skupovi - Dilworthov teorem Postano: 20:32 sub, 11. 9. 2004 Naslov: Re: Parcijalno uredjeni skupovi - Dilworthov teorem |
    |
|
|
[quote="veky"]Nisi definirao što je širina, no pretpostavit ću da je to duljina najduljeg antilanca.[/quote]
Zapravo :) Veljanovom terminologijom to je broj lanaca, duljina najduljeg lanca je "duljina" :)
[quote="veky"]Naravno da ne. Ti imaš u pretpostavci teorema već zadan poset (P,<=) , _čija je širina_ k _već određena_. I ti moraš _toliko_ lanaca proizvesti - ne (nužno) onoliko koliko si imao u pretpostavci indukcije, plus jedan.
Ukoliko bi se dodavanjem novog elementa u poset širina uvijek povećavala za jedan (ie, on bi uvijek bio neusporediv sa svima ostalima), tvoj "dokaz" bi prošao. No naravno, to je, blago rečeno, prejaka pretpostavka. (Grubo rečeno, to je glupost.: )[/quote]
Aaa-Ha :noidea: to me bunilo. <= nije definirano za proizvoljni n+1-clani nadskup, opcenito. Sa druge strane, "proizvoljnost" <=' me donekle umirila jer tako ne bi morao traziti nikakvu "usporednost" (stagod to bilo) sa p.u. <= :-k
ali.. ti tvrdis da kod (n+1)-clanog nadskupa od P ne bi smio imati neki novi k' za sirinu particije lanaca od P' (glavno da je k' prirodan broj? :grebgreb:) ? ili je to poslijedica nesporazuma oko definicije 'sirine'?
[quote="veky"]Hm:?: "Particija u k lanaca" je upravo to, particija. Svaki element mora biti u točno jednom lancu, lanci moraju biti neprazni, i mora ih biti točno k . Tu ništa nisu gornje ili donje ograde, već konkretni iznosi. Ne kužim što ti je "minimalnost broja lanaca".[/quote]
U smislu "minimalne sirine" lanca. Pretpostavljam da takav broj postoji. :-k ovo se, naravno, nadovezuje na gornju opasku o k i k' :?
...naime, koliko shvatim iz definicije lanca, trivijalno particioniranje(ulancavanje :)) nekog konacnog p.u. skupa se moze (bez konflikta sa prof. Darkom :) i neovisno o parcijalnom uredjaju) izvesti tako da uzmem particiju sastavljenu iskljucivo od jednoclanih podskupova ?
[quote="veky"][quote]ili prava vaznost teorema lezi u tvrdnji o lokalno konacnim p.u. skupovima koja se u knjizi nalazi u maloj zagradi na kraju iskaza teorema?[/quote]
Ako te veseli... :-)[/quote]
Ne isuvise :D
[quote="veky"]Još uvijek ima ljudî koji tvrde da je matematika znanost o beskonačnom, i da je konačno uvijek trivijalno. Takvi očito nisu vidjeli Ramseyevu teoriju... :shock: ;-)[/quote]
mozda je problem u odabiru materijala na ovom studiju, ali "konacne" teorije su mi do sada zadavale mnogo vise glavobolja od "beskonacnih" :roll:
[quote="veky"]Otkud ti pak takva ideja sad?
_segmenti_ su konačni (u lofi-posetu). _lanci_, naravno, ne moraju biti.
Evo ti trivijalni primjer: |Z . Standardni uređaj. toset . Širina 1 (svi su usporedivi). Naravno, cijeli je jedan lanac. Beskonačan, ofcourse.
Ali je lokalno konačan. Između svaka dva cijela broja ima konačno mnogo cijelih brojeva..[/quote]
istina, istina, pobrkani loncic :)
| veky (napisa): | | Nisi definirao što je širina, no pretpostavit ću da je to duljina najduljeg antilanca. |
Zapravo  Veljanovom terminologijom to je broj lanaca, duljina najduljeg lanca je "duljina" Veljanovom terminologijom to je broj lanaca, duljina najduljeg lanca je "duljina" 
| veky (napisa): | Naravno da ne. Ti imaš u pretpostavci teorema već zadan poset (P,⇐) , _čija je širina_ k _već određena_. I ti moraš _toliko_ lanaca proizvesti - ne (nužno) onoliko koliko si imao u pretpostavci indukcije, plus jedan.
Ukoliko bi se dodavanjem novog elementa u poset širina uvijek povećavala za jedan (ie, on bi uvijek bio neusporediv sa svima ostalima), tvoj "dokaz" bi prošao. No naravno, to je, blago rečeno, prejaka pretpostavka. (Grubo rečeno, to je glupost.: ) |
Aaa-Ha  to me bunilo. ⇐ nije definirano za proizvoljni n+1-clani nadskup, opcenito. Sa druge strane, "proizvoljnost" ⇐' me donekle umirila jer tako ne bi morao traziti nikakvu "usporednost" (stagod to bilo) sa p.u. ⇐ to me bunilo. ⇐ nije definirano za proizvoljni n+1-clani nadskup, opcenito. Sa druge strane, "proizvoljnost" ⇐' me donekle umirila jer tako ne bi morao traziti nikakvu "usporednost" (stagod to bilo) sa p.u. ⇐ 
ali.. ti tvrdis da kod (n+1)-clanog nadskupa od P ne bi smio imati neki novi k' za sirinu particije lanaca od P' (glavno da je k' prirodan broj?  ) ? ili je to poslijedica nesporazuma oko definicije 'sirine'? ) ? ili je to poslijedica nesporazuma oko definicije 'sirine'?
| veky (napisa): | | Hm:?: "Particija u k lanaca" je upravo to, particija. Svaki element mora biti u točno jednom lancu, lanci moraju biti neprazni, i mora ih biti točno k . Tu ništa nisu gornje ili donje ograde, već konkretni iznosi. Ne kužim što ti je "minimalnost broja lanaca". |
U smislu "minimalne sirine" lanca. Pretpostavljam da takav broj postoji.  ovo se, naravno, nadovezuje na gornju opasku o k i k' ovo se, naravno, nadovezuje na gornju opasku o k i k' 
...naime, koliko shvatim iz definicije lanca, trivijalno particioniranje(ulancavanje  ) nekog konacnog p.u. skupa se moze (bez konflikta sa prof. Darkom ) nekog konacnog p.u. skupa se moze (bez konflikta sa prof. Darkom  i neovisno o parcijalnom uredjaju) izvesti tako da uzmem particiju sastavljenu iskljucivo od jednoclanih podskupova ? i neovisno o parcijalnom uredjaju) izvesti tako da uzmem particiju sastavljenu iskljucivo od jednoclanih podskupova ?
| veky (napisa): | | Citat: | | ili prava vaznost teorema lezi u tvrdnji o lokalno konacnim p.u. skupovima koja se u knjizi nalazi u maloj zagradi na kraju iskaza teorema? |
Ako te veseli...  |
Ne isuvise 
| veky (napisa): | Još uvijek ima ljudî koji tvrde da je matematika znanost o beskonačnom, i da je konačno uvijek trivijalno. Takvi očito nisu vidjeli Ramseyevu teoriju...   |
mozda je problem u odabiru materijala na ovom studiju, ali "konacne" teorije su mi do sada zadavale mnogo vise glavobolja od "beskonacnih" 
| veky (napisa): | Otkud ti pak takva ideja sad?
_segmenti_ su konačni (u lofi-posetu). _lanci_, naravno, ne moraju biti.
Evo ti trivijalni primjer: |Z . Standardni uređaj. toset . Širina 1 (svi su usporedivi). Naravno, cijeli je jedan lanac. Beskonačan, ofcourse.
Ali je lokalno konačan. Između svaka dva cijela broja ima konačno mnogo cijelih brojeva.. |
istina, istina, pobrkani loncic 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk 
Zadnja promjena: ZELENIZUBNAPLANETIDOSADE; 20:43 sub, 11. 9. 2004; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 20:36 sub, 11. 9. 2004 Naslov: Re: Parcijalno uredjeni skupovi - Dilworthov teorem Postano: 20:36 sub, 11. 9. 2004 Naslov: Re: Parcijalno uredjeni skupovi - Dilworthov teorem |
    |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"]Dilworthov teorem:
Neka je [latex](P, \le)[/latex] konacan p.u. skup sirine k. Tada postoji particija od P u k lanaca [latex]C_1, ..., C_k[/latex].[/quote]
[quote="ZELENIZUBNAPLANETIDOSADE"]napomena: nigdje nije napomenut nikakav uvijet za minimalnost broja lanaca :?[/quote]
Zapravo je k najmanji broj lanaca u koje se P može particionirati.
Kad bi se P mogao particionirati u l<k lanaca, onda bi svaki k-člani podskup od P (po Dirichletovom principu :) ) imao barem dva elementa u istom lancu, tj. ne bi mogao biti antilanac. To je u kontradikciji s činjenicom da je širina od P jednaka k.
Konačni p.u. skup se trivijalno može particionirati u konačno mnogo lanaca (npr. njih |P|), ali Dilworthov teorem nam kaže u koliko najmanje (u terminima njegove širine).
Onako kako si ga ti iskazao teorem zapravo daje gornju ocjenu za "najmanji broj lanaca..." (premda zapravo čak znamo točnu vrijednost).
| ZELENIZUBNAPLANETIDOSADE (napisa): | Dilworthov teorem:
Neka je 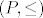 konacan p.u. skup sirine k. Tada postoji particija od P u k lanaca konacan p.u. skup sirine k. Tada postoji particija od P u k lanaca  . . |
| ZELENIZUBNAPLANETIDOSADE (napisa): | napomena: nigdje nije napomenut nikakav uvijet za minimalnost broja lanaca  |
Zapravo je k najmanji broj lanaca u koje se P može particionirati.
Kad bi se P mogao particionirati u l<k lanaca, onda bi svaki k-člani podskup od P (po Dirichletovom principu  ) imao barem dva elementa u istom lancu, tj. ne bi mogao biti antilanac. To je u kontradikciji s činjenicom da je širina od P jednaka k. ) imao barem dva elementa u istom lancu, tj. ne bi mogao biti antilanac. To je u kontradikciji s činjenicom da je širina od P jednaka k.
Konačni p.u. skup se trivijalno može particionirati u konačno mnogo lanaca (npr. njih |P|), ali Dilworthov teorem nam kaže u koliko najmanje (u terminima njegove širine).
Onako kako si ga ti iskazao teorem zapravo daje gornju ocjenu za "najmanji broj lanaca..." (premda zapravo čak znamo točnu vrijednost).
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 20:42 sub, 11. 9. 2004 Naslov: Re: Parcijalno uredjeni skupovi - Dilworthov teorem Postano: 20:42 sub, 11. 9. 2004 Naslov: Re: Parcijalno uredjeni skupovi - Dilworthov teorem |
    |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"][quote="veky"]Nisi definirao što je širina, no pretpostavit ću da je to duljina najduljeg antilanca.[/quote]
Zapravo :) Veljanovom terminologijom to je broj lanaca, duljina najduljeg lanca je "duljina" :) [/quote]
Pa sad ti je veky rekao. Širina od P je najveći kardinalitet (veličina) antilanca u P. Kasnije se pokazuje da je to nečemu jednako... (ali ne ovome što si ti napisao).
[quote="ZELENIZUBNAPLANETIDOSADE"]U smislu "minimalne sirine" lanca. Pretpostavljam da takav broj postoji. :-k ovo se, naravno, nadovezuje na gornju opasku o k i k' :?
...naime, koliko shvatim iz definicije lanca, trivijalno particioniranje(ulancavanje :)) nekog konacnog p.u. skupa se moze (bez konflikta sa prof. Darkom :)) izvesti tako da uzmem particiju sastavljenu iskljucivo od jednoclanih podskupova ?[/quote]
Kakva sad "minimalna širina". Rekli smo što je širina. Za konačne P je ona dobro definirana: gledaš kardinalitete svih antilanaca u P (ima ih najviše 2^|P|) i uzmeš najveći od tih brojeva.
| ZELENIZUBNAPLANETIDOSADE (napisa): | | veky (napisa): | | Nisi definirao što je širina, no pretpostavit ću da je to duljina najduljeg antilanca. |
Zapravo  Veljanovom terminologijom to je broj lanaca, duljina najduljeg lanca je "duljina" Veljanovom terminologijom to je broj lanaca, duljina najduljeg lanca je "duljina"  |
Pa sad ti je veky rekao. Širina od P je najveći kardinalitet (veličina) antilanca u P. Kasnije se pokazuje da je to nečemu jednako... (ali ne ovome što si ti napisao).
| ZELENIZUBNAPLANETIDOSADE (napisa): | U smislu "minimalne sirine" lanca. Pretpostavljam da takav broj postoji.  ovo se, naravno, nadovezuje na gornju opasku o k i k' ovo se, naravno, nadovezuje na gornju opasku o k i k' 
...naime, koliko shvatim iz definicije lanca, trivijalno particioniranje(ulancavanje  ) nekog konacnog p.u. skupa se moze (bez konflikta sa prof. Darkom ) nekog konacnog p.u. skupa se moze (bez konflikta sa prof. Darkom  ) izvesti tako da uzmem particiju sastavljenu iskljucivo od jednoclanih podskupova ? ) izvesti tako da uzmem particiju sastavljenu iskljucivo od jednoclanih podskupova ? |
Kakva sad "minimalna širina". Rekli smo što je širina. Za konačne P je ona dobro definirana: gledaš kardinalitete svih antilanaca u P (ima ih najviše 2^|P|) i uzmeš najveći od tih brojeva.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
|
| [Vrh] |
|
|






