| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 20:33 ned, 12. 9. 2004 Naslov: Egzistencija lijevog inverza u algebri incidencije p.u.skupa |
    |
|
|
Za neupucene, imamo parcijalno uredjen skup (P, <=) i on je lokalno konacan, po oznakama i definicijama iz [url=http://degiorgi.math.hr/forum/viewtopic.php?t=2646]topica o Dillworthovom teoremu i p.u. skupovima[/url].
Definiramo "algebru incidencije" A(P) koja ce "odrazavati strukturu" gornjeg p.u. skupa cije elemente zovemo fjama incidencije ovako:
[latex]A(P) = \{ f : P \times P \rightarrow C | x !\leq y \Rightarrow f(x,y)=0 \}[/latex]
(!<= jest \nleq, tj "nije manje ili jednako", ali \nleq ne radi :()
Nadalje, mnozenje f*g fja iz A(P) zovemo konvolucija i definiramo ga:
[latex](f*g)(x,y):=\sum_{x \leq z \leq y} f(x,z)g(z,y)[/latex]
Shodno tome definira se i jedinicni element:
[latex]\delta(x,y)= \left \{ \begin{array}{cl} 1 & ~, ~x=y \\ 0 & ~, ~x \neq y \end{array} \right.[/latex]
...i onda imamo propoziciju o egzistenciji lijevog, tj. desnog tj. obostranog inverza, koja kaze da za f iz A(P) vrijede ekvivalentne tvrdnje:
a) f ima lijevi inverz
b) f ima desni inverz
c) f ima obostrani inverz
d) f(x,x)!=0 za sve x iz P
Dokaz: iz definicije konvolucije odmah slijedi da je postojanje lijevog inverza ekvivalentno postojanju fje npr. g iz A(P) t.d. f(x,x)g(x,x)=1 za sve x, i to je jasno. Ono sto nije jasno jest "onaj drugi uvijet" :roll: na fju g, a taj jest:
[latex]g(x,y)= - \frac{1}{f(x,x)} \sum_{z < x \leq y}f(x,z)g(z,y) \forall x < y~\_u\_P~[/latex]
Dakle, pitanje: :tso: kako je dobri covjek dosao do gornjeg zakljucka o izgledu lijevog inverza za slucaj x<y i sto me sprijecava da definiram g(x,y)=0 za x<y i rijesim problem inverza? :? takva bi fja bila element iz A(P) i multiplicirana slijeva sa f bi dala deltu :noidea: :?
Za neupucene, imamo parcijalno uredjen skup (P, ⇐) i on je lokalno konacan, po oznakama i definicijama iz topica o Dillworthovom teoremu i p.u. skupovima.
Definiramo "algebru incidencije" A(P) koja ce "odrazavati strukturu" gornjeg p.u. skupa cije elemente zovemo fjama incidencije ovako:
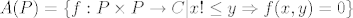
(!⇐ jest \nleq, tj "nije manje ili jednako", ali \nleq ne radi  )
Nadalje, mnozenje f*g fja iz A(P) zovemo konvolucija i definiramo ga:
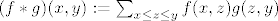
Shodno tome definira se i jedinicni element:
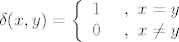
...i onda imamo propoziciju o egzistenciji lijevog, tj. desnog tj. obostranog inverza, koja kaze da za f iz A(P) vrijede ekvivalentne tvrdnje:
a) f ima lijevi inverz
b) f ima desni inverz
c) f ima obostrani inverz
d) f(x,x)!=0 za sve x iz P
Dokaz: iz definicije konvolucije odmah slijedi da je postojanje lijevog inverza ekvivalentno postojanju fje npr. g iz A(P) t.d. f(x,x)g(x,x)=1 za sve x, i to je jasno. Ono sto nije jasno jest "onaj drugi uvijet"  na fju g, a taj jest:
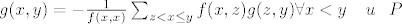
Dakle, pitanje:  kako je dobri covjek dosao do gornjeg zakljucka o izgledu lijevog inverza za slucaj x<y i sto me sprijecava da definiram g(x,y)=0 za x<y i rijesim problem inverza?  takva bi fja bila element iz A(P) i multiplicirana slijeva sa f bi dala deltu 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
veky
Forumaš(ica)
Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
| Postano: 13:22 pon, 13. 9. 2004 Naslov: Re: Egzistencija lijevog inverza u algebri incidencije p.u.s |
|
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"]Za neupucene, imamo parcijalno uredjen skup (P, <=) i on je lokalno konacan, po oznakama i definicijama iz [url=http://degiorgi.math.hr/forum/viewtopic.php?t=2646]topica o Dillworthovom teoremu i p.u. skupovima[/url].
Definiramo "algebru incidencije" A(P) koja ce "odrazavati strukturu" gornjeg p.u. skupa cije elemente zovemo fjama incidencije ovako:
[latex]A(P) = \{ f : P \times P \rightarrow C | x !\leq y \Rightarrow f(x,y)=0 \}[/latex]
(!<= jest \nleq, tj "nije manje ili jednako", ali \nleq ne radi :()[/quote]
Da probaš s \not\leq ? :-)
((Ja sam čak i != pisao pomoću \not= , dok mi Ksenija nije rekla da postoji i \neq . Ah ta ortogonalnost...: ))
[quote]Nadalje, mnozenje f*g fja iz A(P) zovemo konvolucija i definiramo ga:
[latex](f*g)(x,y):=\sum_{x \leq z \leq y} f(x,z)g(z,y)[/latex]
Shodno tome definira se i jedinicni element:
[latex]\delta(x,y)= \left \{ \begin{array}{cl} 1 & ~, ~x=y \\ 0 & ~, ~x \neq y \end{array} \right.[/latex]
...i onda imamo propoziciju o egzistenciji lijevog, tj. desnog tj. obostranog inverza, koja kaze da za f iz A(P) vrijede ekvivalentne tvrdnje:
a) f ima lijevi inverz
b) f ima desni inverz
c) f ima obostrani inverz
d) f(x,x)!=0 za sve x iz P
Dokaz: iz definicije konvolucije odmah slijedi da je postojanje lijevog inverza ekvivalentno postojanju fje npr. g iz A(P) t.d. f(x,x)g(x,x)=1 za sve x, i to je jasno. Ono sto nije jasno jest "onaj drugi uvijet" :roll: na fju g, a taj jest:
[latex]g(x,y)= - \frac{1}{f(x,x)} \sum_{z < x \leq y}f(x,z)g(z,y) \forall x < y~\_u\_P~[/latex]
Dakle, pitanje: :tso: kako je dobri covjek dosao do gornjeg zakljucka o izgledu lijevog inverza za slucaj x<y i sto me sprijecava da definiram g(x,y)=0 za x<y i rijesim problem inverza? :? takva bi fja bila element iz A(P) i multiplicirana slijeva sa f bi dala deltu :noidea: :?[/quote]
Ali koliko ja kužim stvar, on želi definirati obostrani inverz. Nekako mi se ne čini da bi ovo bio i desni inverz...
| ZELENIZUBNAPLANETIDOSADE (napisa): | Za neupucene, imamo parcijalno uredjen skup (P, ⇐) i on je lokalno konacan, po oznakama i definicijama iz topica o Dillworthovom teoremu i p.u. skupovima.
Definiramo "algebru incidencije" A(P) koja ce "odrazavati strukturu" gornjeg p.u. skupa cije elemente zovemo fjama incidencije ovako:
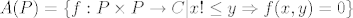
(!⇐ jest \nleq, tj "nije manje ili jednako", ali \nleq ne radi ) |
Da probaš s \not\leq ? 
((Ja sam čak i != pisao pomoću \not= , dok mi Ksenija nije rekla da postoji i \neq . Ah ta ortogonalnost...: ))
| Citat: | Nadalje, mnozenje f*g fja iz A(P) zovemo konvolucija i definiramo ga:
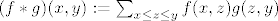
Shodno tome definira se i jedinicni element:
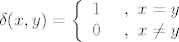
...i onda imamo propoziciju o egzistenciji lijevog, tj. desnog tj. obostranog inverza, koja kaze da za f iz A(P) vrijede ekvivalentne tvrdnje:
a) f ima lijevi inverz
b) f ima desni inverz
c) f ima obostrani inverz
d) f(x,x)!=0 za sve x iz P
Dokaz: iz definicije konvolucije odmah slijedi da je postojanje lijevog inverza ekvivalentno postojanju fje npr. g iz A(P) t.d. f(x,x)g(x,x)=1 za sve x, i to je jasno. Ono sto nije jasno jest "onaj drugi uvijet" na fju g, a taj jest:
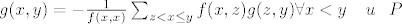
Dakle, pitanje: kako je dobri covjek dosao do gornjeg zakljucka o izgledu lijevog inverza za slucaj x<y i sto me sprijecava da definiram g(x,y)=0 za x<y i rijesim problem inverza? takva bi fja bila element iz A(P) i multiplicirana slijeva sa f bi dala deltu |
Ali koliko ja kužim stvar, on želi definirati obostrani inverz. Nekako mi se ne čini da bi ovo bio i desni inverz...
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 13:58 pon, 13. 9. 2004 Naslov: Re: Egzistencija lijevog inverza u algebri incidencije p.u.s |
|
|
|
[quote="veky"]Da probaš s \not\leq ? :-)[/quote]
[latex]\not\leq[/latex] :D
[quote="veky"][quote]Dokaz: iz definicije konvolucije odmah slijedi da je postojanje lijevog inverza ekvivalentno postojanju fje npr. g iz A(P) t.d. f(x,x)g(x,x)=1 za sve x, i to je jasno. Ono sto nije jasno jest "onaj drugi uvijet" :roll: na fju g, a taj jest:
[latex]g(x,y)= - \frac{1}{f(x,x)} \sum_{z < x \leq y}f(x,z)g(z,y) \forall x < y~\_u\_P~[/latex]
Dakle, pitanje: :tso: kako je dobri covjek dosao do gornjeg zakljucka o izgledu lijevog inverza za slucaj x<y i sto me sprijecava da definiram g(x,y)=0 za x<y i rijesim problem inverza? :? takva bi fja bila element iz A(P) i multiplicirana slijeva sa f bi dala deltu :noidea: :?[/quote]
Ali koliko ja kužim stvar, on želi definirati obostrani inverz. Nekako mi se ne čini da bi ovo bio i desni inverz...[/quote]
Ne znam :shock: za x=y slucaj se slazemo, al za x<y mi se nekako cini da bi nulfja u onoj sumi gore na kraju dala nulu bez obzira na to dal je slijeva ili sdesna :? Jedino ako bi doticni inverz rusio neke lijepe stvari o strukturi algebre sa obzirom na sumu fja i mnozenje skalarom kojih ja u ovom trenutku nisam svijestan?
Veljan za slucaj x<y pise:
[latex]g(x,y)= - \frac{1}{f(x,x)} \sum_{z < x \leq y}f(x,z)g(z,y)[/latex]
Jel Veljan mozda tipfelerio kada pise da je z<x<=y :?: Pretpostavka na P jest da je on samo lokalno konacan, drugim rijecima suma z<x<=<y ne mora postojati? no sa druge strane suma po x<z<=y bi jos i imala nekakvog smisla u ovom kontekstu?
Onaj 1/f(x,x) sugerira da je covjek zelio na, neki nacin, "normalizirati" inverznu fju iako to (bar sto se inverza tice i slucaja x<y) ne bi smjelo imati nikakvog efekta. Ili je to nepisana nakana da se tako formuliran g(x,y) definira _za svaki_ x,y a ne samo x<y :?: (pa je onaj dio o za svaki x<y samo prvi korak u takvom rezoniranju, pa su ostali koraci presuceni? ili se radi o koraku za cuvanje onog moguceg problema sa narusavanjem drugih svojstava algebre o kojima jos nisam posteno razmislio?)
I jos dodatno buni onaj "-" prije cijelog izraza :shock: Koju mu je... patiku :D on trebao :?: :shock:
Ako bih isao mnoziti sa lijeva Veljanovu ispravljenu(?) g(x,y) sa f iz pretpostavke propozicije, dobio bih dosta ruznu rekurziju, koja me bar na prvi pogled nece dovesti do rijesenja propozicije u kratkom nizu jednostavnih elementarnih tvrdnji.
U tom slucaju, da li da jednostavno uvrstim tu "formulu" medju "eksterne memorije" i pretpostavim da je rijec "Dokaz." koja pise iznad tog teksta cin pjesnickog oduska autora ili da trosim dodatno vrijeme na to dva dana prije komisije u nadi da ce mi to donijeti nakakav dodatni insight a ne ekstrakt beskorisne frustracije? :evil:
:grrr: :boliglava: :bad-words: :headbanging: :sillyroll: :verycool: :cry: :roll:
| veky (napisa): | | Da probaš s \not\leq ? |
 
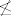
| veky (napisa): | | Citat: | Dokaz: iz definicije konvolucije odmah slijedi da je postojanje lijevog inverza ekvivalentno postojanju fje npr. g iz A(P) t.d. f(x,x)g(x,x)=1 za sve x, i to je jasno. Ono sto nije jasno jest "onaj drugi uvijet" na fju g, a taj jest:
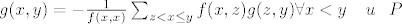
Dakle, pitanje: kako je dobri covjek dosao do gornjeg zakljucka o izgledu lijevog inverza za slucaj x<y i sto me sprijecava da definiram g(x,y)=0 za x<y i rijesim problem inverza? takva bi fja bila element iz A(P) i multiplicirana slijeva sa f bi dala deltu |
Ali koliko ja kužim stvar, on želi definirati obostrani inverz. Nekako mi se ne čini da bi ovo bio i desni inverz... |
Ne znam  za x=y slucaj se slazemo, al za x<y mi se nekako cini da bi nulfja u onoj sumi gore na kraju dala nulu bez obzira na to dal je slijeva ili sdesna Jedino ako bi doticni inverz rusio neke lijepe stvari o strukturi algebre sa obzirom na sumu fja i mnozenje skalarom kojih ja u ovom trenutku nisam svijestan?
Veljan za slucaj x<y pise:
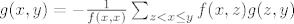
Jel Veljan mozda tipfelerio kada pise da je z<x⇐y  Pretpostavka na P jest da je on samo lokalno konacan, drugim rijecima suma z<x⇐<y ne mora postojati? no sa druge strane suma po x<z⇐y bi jos i imala nekakvog smisla u ovom kontekstu?
Onaj 1/f(x,x) sugerira da je covjek zelio na, neki nacin, "normalizirati" inverznu fju iako to (bar sto se inverza tice i slucaja x<y) ne bi smjelo imati nikakvog efekta. Ili je to nepisana nakana da se tako formuliran g(x,y) definira _za svaki_ x,y a ne samo x<y (pa je onaj dio o za svaki x<y samo prvi korak u takvom rezoniranju, pa su ostali koraci presuceni? ili se radi o koraku za cuvanje onog moguceg problema sa narusavanjem drugih svojstava algebre o kojima jos nisam posteno razmislio?)
I jos dodatno buni onaj "-" prije cijelog izraza Koju mu je... patiku on trebao
Ako bih isao mnoziti sa lijeva Veljanovu ispravljenu(?) g(x,y) sa f iz pretpostavke propozicije, dobio bih dosta ruznu rekurziju, koja me bar na prvi pogled nece dovesti do rijesenja propozicije u kratkom nizu jednostavnih elementarnih tvrdnji.
U tom slucaju, da li da jednostavno uvrstim tu "formulu" medju "eksterne memorije" i pretpostavim da je rijec "Dokaz." koja pise iznad tog teksta cin pjesnickog oduska autora ili da trosim dodatno vrijeme na to dva dana prije komisije u nadi da ce mi to donijeti nakakav dodatni insight a ne ekstrakt beskorisne frustracije? 
      
_________________
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 20:42 uto, 14. 9. 2004 Naslov: |
|
|
|
OK :)
Thnx to veky :bow: rijesili i taj problem, dakle, veljan jest pobrkao koncice sa onim z<x<=<y i uistinu treba stajati na tom mjestu x<z<=y a postupak dobivanja onog izraza jest slijedeci (i ipak ne tako strasan ;))
Dakle, trazimo fju (g) iz A(P) koja bi, mnozenjem sa lijeva fje f iz A(P) dala 1-nicnu fju "delta" (iz gornjeg teksta):
[latex](g*f)(x,y) = \displaystyle \sum_{x \leq z \leq y}f(x,z)g(z,y) = \delta(x,y) \Longrightarrow \\
g(x,x)f(x,x)=1~, ~\forall x \in P$ i $(*)$ $g(x,y)f(x,y)=0~, ~\forall x<y[/latex]
(za x>y su fjske vrijednosti obije fje jednake 0 ovako i onako)
Izlucimo prvi clan sume:
[latex]~(*) ~ \Rightarrow \displaystyle \sum_{x \leq z \leq y} f(x,z)g(z,y) = f(x,x)g(x,y) + \sum_{x < z \leq y}f(x,z)g(z,y) = 0[/latex]
...i dalje je samo stvar prebacivanja cijele sume na desnu stranu i dijeljenja sa f(x,x) (koji je != 0), dakle:
[latex] g(x,y)=\displaystyle -\frac{1}{f(x,x)} \sum_{x < z \leq y}f(x,z)g(z,y)[/latex]
...i jos jedna notacija za konvoluciju f*g:
[latex](f*g)(x,y) = \displaystyle \sum_{z \in P} f(x,z)g(z,y)[/latex], buduci da je f(x,z)=0 ako je z<x i g(z,y)=0 ako je z>y, tako da je uvijet x<=z<=y, u biti, suvisan :)
Eto :D fala veky :D
OK
Thnx to veky  rijesili i taj problem, dakle, veljan jest pobrkao koncice sa onim z<x⇐<y i uistinu treba stajati na tom mjestu x<z⇐y a postupak dobivanja onog izraza jest slijedeci (i ipak ne tako strasan )
Dakle, trazimo fju (g) iz A(P) koja bi, mnozenjem sa lijeva fje f iz A(P) dala 1-nicnu fju "delta" (iz gornjeg teksta):
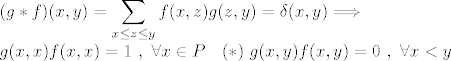
(za x>y su fjske vrijednosti obije fje jednake 0 ovako i onako)
Izlucimo prvi clan sume:
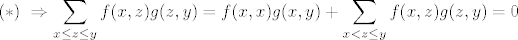
...i dalje je samo stvar prebacivanja cijele sume na desnu stranu i dijeljenja sa f(x,x) (koji je != 0), dakle:
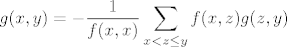
...i jos jedna notacija za konvoluciju f*g:
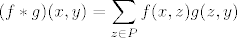 , buduci da je f(x,z)=0 ako je z<x i g(z,y)=0 ako je z>y, tako da je uvijet x⇐z⇐y, u biti, suvisan
Eto fala veky
_________________
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
|
