|
oukej....ti zapravo trazis tangencijalnu ravninu na sferu radijusa 1, oko tocke (1, 2, 3), paralelnu s y osi. nekako se odma vidi da se moze takva ravnina "naslonit" na takovu jednu sferu.
to ce biti tangencijalna ravnina u nekoj tocci dane sfere, nek se ona zove
[latex]
P_0 = (x_0, y_0, z_0)
[/latex]
znamo:
1. vektor normale tang. ravnine u tocki
[latex]
P_0[/latex] je [latex]
(2x_0 - 2, 2y_0 - 4, 2z_0 - 6)
[/latex] , tj. jednadzba ravnine ce biti oblika:
[latex]
(2x - 2)*(x - x_0) + (2y - 4)*(y - y_0) + (2z - 6)*(z - z_0) = 0
[/latex].
2. vektor (0, 1, 0) je na y osi, koja je sadrzana u ravnini - znaci vektor normale ravnine je okomit na (0, 1, 0)
i 3. ne zaboravimo, tocka [latex]
P_0
[/latex] je i na sferi! :D
sad, iz 2. -> [latex]
2y_0 - 4 = 0
[/latex], tj.
[latex]
y_0 = 2.
[/latex] - super! sad jos fiksirat dva vektora, imamo ravninu!
sad, iz 1. i cinjenice da je tocka (0, 0, 0) na y osi, pa i iz ravnine koju trazimo ->
[latex]
2x_0 + 4y_0 + 6 z_0 = 0
[/latex], tj. [latex]
2x_0 + 8 + 6z_0 = 0.
[/latex]
a iz 3. -> [latex]
( x_0 -1)^2 + 0 + (z_0 - 3)^2=1
[/latex]
to bi trebalo biti dovoljno da lociras tocku(e) [latex]
(x_0, y_0, z_0)
[/latex], a onda lako vidis koja je tocno jednadzba tangencijalne ravnine na danu sferu u toj tocki, npr. iz 1.
eto, mislim da bi prica tako nekako mogla ici. ispricavam se na nepreciznosti glede skupa rijesenja, i sve u svemu losem izrazavanju, najme, jako mi se spava, al ne mogah odoljet koristit latex, sad kad sam napokon shvatila da postoji i polovila osnove :D
valjda ce bit ipak neke koristi od svega!
oukej....ti zapravo trazis tangencijalnu ravninu na sferu radijusa 1, oko tocke (1, 2, 3), paralelnu s y osi. nekako se odma vidi da se moze takva ravnina "naslonit" na takovu jednu sferu.
to ce biti tangencijalna ravnina u nekoj tocci dane sfere, nek se ona zove
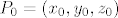
znamo:
1. vektor normale tang. ravnine u tocki
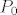 je je 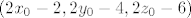 , tj. jednadzba ravnine ce biti oblika: , tj. jednadzba ravnine ce biti oblika:
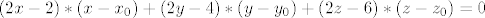 . .
2. vektor (0, 1, 0) je na y osi, koja je sadrzana u ravnini - znaci vektor normale ravnine je okomit na (0, 1, 0)
i 3. ne zaboravimo, tocka 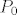 je i na sferi! je i na sferi! 
sad, iz 2. → 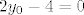 , tj. , tj.
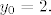 - super! sad jos fiksirat dva vektora, imamo ravninu! - super! sad jos fiksirat dva vektora, imamo ravninu!
sad, iz 1. i cinjenice da je tocka (0, 0, 0) na y osi, pa i iz ravnine koju trazimo →
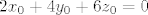 , tj. , tj. 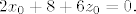
a iz 3. → 
to bi trebalo biti dovoljno da lociras tocku(e) 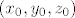 , a onda lako vidis koja je tocno jednadzba tangencijalne ravnine na danu sferu u toj tocki, npr. iz 1. , a onda lako vidis koja je tocno jednadzba tangencijalne ravnine na danu sferu u toj tocki, npr. iz 1.
eto, mislim da bi prica tako nekako mogla ici. ispricavam se na nepreciznosti glede skupa rijesenja, i sve u svemu losem izrazavanju, najme, jako mi se spava, al ne mogah odoljet koristit latex, sad kad sam napokon shvatila da postoji i polovila osnove 
valjda ce bit ipak neke koristi od svega!
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|




