| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 14:33 ned, 3. 10. 2004 Naslov: Ekstr. svojstva spektra sim. matrice, Def1.7 i L1.8 Postano: 14:33 ned, 3. 10. 2004 Naslov: Ekstr. svojstva spektra sim. matrice, Def1.7 i L1.8 |
    |
|
|
[quote="prof. Caklovic u PDF skripti"]Definicija 1.7 Neka su q,f : |R^n --> |R neprekidno diferencijabilne funkcije i M = {y iz |R^n : f(y)=0 }.
Reci cemo da je p iz M kriticna tocka restrikcije [latex]q|_M[/latex] ako za svaku glatku regularnu krivulju [latex]\gamma(t): (-\varepsilon,\varepsilon) \rightarrow M$, $\gamma(0)=p[/latex], vrijedi:
[latex]\displaystyle \left. \frac d{dt}q(\gamma(t))\right |_{t=0}=0 [/latex][/quote]
Nekoliko stvari:
Propustam li nesto u onom [latex](-\varepsilon, \varepsilon)[/latex] ili je profesor "zelio" upotrijebiti ostre zagrade [latex]<-\varepsilon, \varepsilon>[/latex]?
2. kamen smutnje bi bio izraz:
[latex]\displaystyle \left. \frac d{dt}q(\gamma(t))\right |_{t=0}=0[/latex] :shock:
Razumio bih da je profesor dao uvijet:
[latex]q`(\gamma(0))\gamma`(0)=0 [/latex]
za koji se u dokazu leme 1.8 spomene da je jednak gornjem, barem meni, kripticnom izrazu :shock:
Propustam li nesto? :shock:
| prof. Caklovic u PDF skripti (napisa): | Definicija 1.7 Neka su q,f : |R^n → |R neprekidno diferencijabilne funkcije i M = {y iz |R^n : f(y)=0 }.
Reci cemo da je p iz M kriticna tocka restrikcije 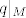 ako za svaku glatku regularnu krivulju ako za svaku glatku regularnu krivulju 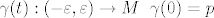 , vrijedi: , vrijedi:
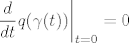 |
Nekoliko stvari:
Propustam li nesto u onom 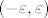 ili je profesor "zelio" upotrijebiti ostre zagrade ili je profesor "zelio" upotrijebiti ostre zagrade 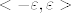 ? ?
2. kamen smutnje bi bio izraz:
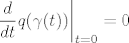 
Razumio bih da je profesor dao uvijet:
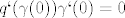
za koji se u dokazu leme 1.8 spomene da je jednak gornjem, barem meni, kripticnom izrazu 
Propustam li nesto? 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 14:50 ned, 3. 10. 2004 Naslov: Re: Ekstr. svojstva spektra sim. matrice, Def1.7 i L1.8 Postano: 14:50 ned, 3. 10. 2004 Naslov: Re: Ekstr. svojstva spektra sim. matrice, Def1.7 i L1.8 |
    |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"][quote="prof. Caklovic u PDF skripti"]Definicija 1.7 Neka su q,f : |R^n --> |R neprekidno diferencijabilne funkcije i M = {y iz |R^n : f(y)=0 }.
Reci cemo da je p iz M kriticna tocka restrikcije [latex]q|_M[/latex] ako za svaku glatku regularnu krivulju [latex]\gamma(t): (-\varepsilon,\varepsilon) \rightarrow M$, $\gamma(0)=p[/latex], vrijedi:
[latex]\displaystyle \left. \frac d{dt}q(\gamma(t))\right |_{t=0}=0 [/latex][/quote]
Nekoliko stvari:
Propustam li nesto u onom [latex](-\varepsilon, \varepsilon)[/latex] ili je profesor "zelio" upotrijebiti ostre zagrade [latex]<-\varepsilon, \varepsilon>[/latex]?[/quote]
Kontemplirati što je prof. Čaklović želio često je prilično transcendentna aktivnost:-), ali da, starije oznake za otvorene intervale su uključivale i stvari poput (a,b) ... pa čak i stvari poput ]a,b[ :blueshock:
[quote]
2. kamen smutnje bi bio izraz:
[latex]\displaystyle \left. \frac d{dt}q(\gamma(t))\right |_{t=0}=0[/latex] :shock:
Razumio bih da je profesor dao uvijet:
[latex]q`(\gamma(0))\gamma`(0)=0 [/latex]
za koji se u dokazu leme 1.8 spomene da je jednak gornjem, barem meni, kripticnom izrazu :shock:
Propustam li nesto? :shock:[/quote]
Pa to je najobičnije lančano pravilo. Taj kriptični izraz je samo drugo ime za derivaciju kompozicije (qogamma)'(0), pogodan za ljude, često fizičarskog backgrounda, koji ne vjeruju u čiste funkcije ( f ) i pišu samo izraze ( f(x) ). Zamisli to kao: žnj(0) , gdje je žnj(t):=d/dt(q(gamma(t))) . Iliti, "de po de te od ku od gama od te, _gdje je_ te jednako nula".
HTH,
| ZELENIZUBNAPLANETIDOSADE (napisa): | | prof. Caklovic u PDF skripti (napisa): | Definicija 1.7 Neka su q,f : |R^n → |R neprekidno diferencijabilne funkcije i M = {y iz |R^n : f(y)=0 }.
Reci cemo da je p iz M kriticna tocka restrikcije 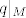 ako za svaku glatku regularnu krivulju ako za svaku glatku regularnu krivulju 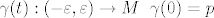 , vrijedi: , vrijedi:
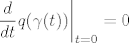 |
Nekoliko stvari:
Propustam li nesto u onom 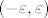 ili je profesor "zelio" upotrijebiti ostre zagrade ili je profesor "zelio" upotrijebiti ostre zagrade 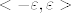 ? ? |
Kontemplirati što je prof. Čaklović želio često je prilično transcendentna aktivnost:-), ali da, starije oznake za otvorene intervale su uključivale i stvari poput (a,b) ... pa čak i stvari poput ]a,b[ 
| Citat: |
2. kamen smutnje bi bio izraz:
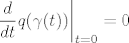 
Razumio bih da je profesor dao uvijet:
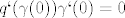
za koji se u dokazu leme 1.8 spomene da je jednak gornjem, barem meni, kripticnom izrazu 
Propustam li nesto?  |
Pa to je najobičnije lančano pravilo. Taj kriptični izraz je samo drugo ime za derivaciju kompozicije (qogamma)'(0), pogodan za ljude, često fizičarskog backgrounda, koji ne vjeruju u čiste funkcije ( f ) i pišu samo izraze ( f(x) ). Zamisli to kao: žnj(0) , gdje je žnj(t):=d/dt(q(gamma(t))) . Iliti, "de po de te od ku od gama od te, _gdje je_ te jednako nula".
HTH,
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 15:03 ned, 3. 10. 2004 Naslov: Re: Ekstr. svojstva spektra sim. matrice, Def1.7 i L1.8 Postano: 15:03 ned, 3. 10. 2004 Naslov: Re: Ekstr. svojstva spektra sim. matrice, Def1.7 i L1.8 |
    |
|
|
[quote="veky"]Pa to je najobičnije lančano pravilo. Taj kriptični izraz je samo drugo ime za derivaciju kompozicije (qogamma)'(0), pogodan za ljude, često fizičarskog backgrounda, koji ne vjeruju u čiste funkcije ( f ) i pišu samo izraze ( f(x) ). Zamisli to kao: žnj(0) , gdje je žnj(t):=d/dt(q(gamma(t))) . Iliti, "de po de te od ku od gama od te, _gdje je_ te jednako nula".
HTH,[/quote]
Phew :) fala veky :) Da bar i ja jednog dana naucim citati ove tekstove :)
| veky (napisa): | Pa to je najobičnije lančano pravilo. Taj kriptični izraz je samo drugo ime za derivaciju kompozicije (qogamma)'(0), pogodan za ljude, često fizičarskog backgrounda, koji ne vjeruju u čiste funkcije ( f ) i pišu samo izraze ( f(x) ). Zamisli to kao: žnj(0) , gdje je žnj(t):=d/dt(q(gamma(t))) . Iliti, "de po de te od ku od gama od te, _gdje je_ te jednako nula".
HTH, |
Phew  fala veky fala veky  Da bar i ja jednog dana naucim citati ove tekstove Da bar i ja jednog dana naucim citati ove tekstove 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 20:51 ned, 3. 10. 2004 Naslov: Re: Ekstr. svojstva spektra sim. matrice, Def1.7 i L1.8 Postano: 20:51 ned, 3. 10. 2004 Naslov: Re: Ekstr. svojstva spektra sim. matrice, Def1.7 i L1.8 |
    |
|
|
[quote="veky"]Od toga nećeš imati neke prevelike koristi. Radije nauči LA-background kako spada. ;-)[/quote]
Istina :) a-wurkin' on it :)
| veky (napisa): | Od toga nećeš imati neke prevelike koristi. Radije nauči LA-background kako spada.  |
Istina  a-wurkin' on it a-wurkin' on it 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
|



