| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 20:16 sri, 20. 10. 2004 Naslov: Re: Prazan skup Postano: 20:16 sri, 20. 10. 2004 Naslov: Re: Prazan skup |
    |
|
|
[quote="Vincent Van Ear"]Prazan skup je (pravi)podskup svakog nepraznog skupa.
To je konvencija?
Nedokazivo?[/quote]
Ne. To je teorem koji se sasvim lijepo može dokazati.
Neka je A bilo kakav neprezan skup. Prvo dokažimo da je 0 (prazan skup) podskup od A .
To bi značilo da za svaki objekt x , činjenica da je x@0 povlači da je x@A . No budući da po definiciji praznog skupa x@0 je uvijek laž (za svaki x ), po definiciji implikacije (laž implicira bilo što), vrijednost gornje izjave je uvijek istina. So, 0 C= A . Da je _pravi_ podskup, to samo znači da nisu jednaki. No to smo upravo rekli kad smo rekli da je A neprazan - dakle nije prazan, odnosno, nije jednak 0 .
[quote]Čemu uopće potreba za definiranjem praznoga skupa,što će mi nešto što ne posjeduje(ili je posjed zanemariv) nikakvu informaciju?[/quote]
? Otkud ti takva ideja?
To što ne posjeduje elemente nikako ne znači da ne posjeduje i informaciju - posjeduje informaciju da nijedan objekt nije njegov element. Baš kao što npr. skup {1,2,3} ne posjeduje samo informacije tipa "3 je njegov element", već i informacije tipa "4 nije njegov element".
Skup je nešto što za svaki objekt može jednoznačno odgovoriti je li taj objekt njegov element, ili nije. Prazan skup je samo poseban po tome što na sva ta pitanja odgovara jednako - negativno.
HTH,
| Vincent Van Ear (napisa): | Prazan skup je (pravi)podskup svakog nepraznog skupa.
To je konvencija?
Nedokazivo? |
Ne. To je teorem koji se sasvim lijepo može dokazati.
Neka je A bilo kakav neprezan skup. Prvo dokažimo da je 0 (prazan skup) podskup od A .
To bi značilo da za svaki objekt x , činjenica da je x@0 povlači da je x@A . No budući da po definiciji praznog skupa x@0 je uvijek laž (za svaki x ), po definiciji implikacije (laž implicira bilo što), vrijednost gornje izjave je uvijek istina. So, 0 C= A . Da je _pravi_ podskup, to samo znači da nisu jednaki. No to smo upravo rekli kad smo rekli da je A neprazan - dakle nije prazan, odnosno, nije jednak 0 .
| Citat: | | Čemu uopće potreba za definiranjem praznoga skupa,što će mi nešto što ne posjeduje(ili je posjed zanemariv) nikakvu informaciju? |
? Otkud ti takva ideja?
To što ne posjeduje elemente nikako ne znači da ne posjeduje i informaciju - posjeduje informaciju da nijedan objekt nije njegov element. Baš kao što npr. skup {1,2,3} ne posjeduje samo informacije tipa "3 je njegov element", već i informacije tipa "4 nije njegov element".
Skup je nešto što za svaki objekt može jednoznačno odgovoriti je li taj objekt njegov element, ili nije. Prazan skup je samo poseban po tome što na sva ta pitanja odgovara jednako - negativno.
HTH,
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 21:51 sri, 20. 10. 2004 Naslov: Postano: 21:51 sri, 20. 10. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"][quote] Ne. To je teorem koji se sasvim lijepo može dokazati. [/quote]
Zašto na predavanjima nije rečeno da se radi o teoremu.Zašto tako važna činjenica(ipak je na vrhu hijerarhije-teorem) iznjedri iz nekakve napomene(nije da omalovažavam napomene ali teorem je ipak ''Faraon'' :D ) ?[/quote]
Zato što nije riječ o teoremu koji je naročito važan za teoriju koja se u tom trenutku razvija (elementarna matematika). Možda te zbunila moja uptreba riječi "teorem", koju sam objasnio kad su me prošle godine na ovom forumu optužili da na vježbama "dokazujem teoreme" ( http://degiorgi.math.hr/forum/viewtopic.php?p=9008#9008 ) - ja sam logičar. Meni je teorem ono što se može dokazati. Leme, Korolari, Propozicije, argumentirane Tvrdnje - sve su to teoremi ako imaju dokaz. Unutar neke "akademske" teorije, pojam "Teorem" se obično rezervira za nekoliko centralnih tvrdnji teorije, "Faraone" što bi ti rekao. :-)
[quote][quote] ? Otkud ti takva ideja? [/quote]
Znaš me :mrgreen:[/quote]
Mda. Ali se svejedno uvijek iznova iznenadim. ;-o
[quote]Dakle čemu potreba za uvođenjem praznog skupa ?
Nije da je u praksi negdje bio potreban :),[/quote]
Jest (zapravo, ovisi što smatraš pod "praksom": ), samo što se to obično ne priča na prvoj godini - saznat ćeš to tamo negdje na trećoj ako te bude zanimalo, na kolegiju Teorija skupova.
Ukratko, u TS su _svi_ objekti skupovi. Dakle, elementi skupova su isto skupovi. Mislim da je sasvim jasno da na taj način jedini skup kojeg možeš a priori imati je upravo prazan skup, označen s 0 . Nakon toga možeš stvoriti skup čiji će jedini element biti prazan skup, dakle {0} , označen 1 . Onda možeš stvarati razne skupove pomoću 0 i 1 - npr. možeš stvoriti njihov par, {0,1} , označen 2 . I tako dalje... sve do realnih brojeva. A možeš i dalje... ;-)
[quote]jeli stvoren iz čiste slobodoumnosti ili se netko pitao što je komplement univerzalnog skupa ?[/quote]
Prije bih rekao da je "univerzalni skup" pojam koji je nastao u pokušaju (aproksimativnog) odgovaranja na pitanje što je komplement praznog skupa. Prazan skup je jedinstven (svi prazni skupovi su jednaki - probaj to dokazati: ), dok univerzalni skup nije. Svaka teorija ima neki svoj univerzalni skup u kojem radi. "Pravi" komplement praznog skupa ne postoji u standardnoj teoriji skupova. "Skup svega" je oksiomoron - to jednostavno nije skup.
[quote]I još nešto,zar je lakše riješiti veliki Fermat-ov problem nego definirati skup ?[/quote]
Je li lakše shvatiti Zen ili podići 800kg ? ;-D
Mislim da shvaćaš što hoću reći... to su različite vrste težine. Dokaz FLTa je čisto matematička stvar - definicija skupa je metamatematički problem.
[quote]Gdje nastaju problemi ?[/quote]
Pitanje na koje bi se moglo duugo odgovarati (pročitaj npr. početak http://web.math.hr/~veky/em/vjezbe/skupovi.html ), no evo ti ovo za početak. Definicija bi trebala imati prvi općenitiji pojam, i vrsnu razliku, zar ne? E pa, skupovi su (intentionally) toliko općeniti da "prvi općenitiji pojam" baš i ne postoji. Često se skup "definira" kao "kolekcija elemenata kod koje...", kao da je "kolekcija" nešto još općenitije od skupa. Možda, ali "kolekcija" (možda baš zato:!:) nije matematički pojam - to može služiti samo kao intuitivna definicija. Ne možemo imati i :ovca: i :money: - i definirati skup preko ostalih math-pojmova, i definirati sve ostale math-pojmove pomoću skupova.
HTH,
| Vincent Van Ear (napisa): | | Citat: | | Ne. To je teorem koji se sasvim lijepo može dokazati. |
Zašto na predavanjima nije rečeno da se radi o teoremu.Zašto tako važna činjenica(ipak je na vrhu hijerarhije-teorem) iznjedri iz nekakve napomene(nije da omalovažavam napomene ali teorem je ipak ''Faraon''  ) ? ) ? |
Zato što nije riječ o teoremu koji je naročito važan za teoriju koja se u tom trenutku razvija (elementarna matematika). Možda te zbunila moja uptreba riječi "teorem", koju sam objasnio kad su me prošle godine na ovom forumu optužili da na vježbama "dokazujem teoreme" ( http://degiorgi.math.hr/forum/viewtopic.php?p=9008#9008 ) - ja sam logičar. Meni je teorem ono što se može dokazati. Leme, Korolari, Propozicije, argumentirane Tvrdnje - sve su to teoremi ako imaju dokaz. Unutar neke "akademske" teorije, pojam "Teorem" se obično rezervira za nekoliko centralnih tvrdnji teorije, "Faraone" što bi ti rekao. 
| Citat: | | Citat: | | ? Otkud ti takva ideja? |
Znaš me  |
Mda. Ali se svejedno uvijek iznova iznenadim. ;-o
| Citat: | Dakle čemu potreba za uvođenjem praznog skupa ?
Nije da je u praksi negdje bio potreban  , , |
Jest (zapravo, ovisi što smatraš pod "praksom": ), samo što se to obično ne priča na prvoj godini - saznat ćeš to tamo negdje na trećoj ako te bude zanimalo, na kolegiju Teorija skupova.
Ukratko, u TS su _svi_ objekti skupovi. Dakle, elementi skupova su isto skupovi. Mislim da je sasvim jasno da na taj način jedini skup kojeg možeš a priori imati je upravo prazan skup, označen s 0 . Nakon toga možeš stvoriti skup čiji će jedini element biti prazan skup, dakle {0} , označen 1 . Onda možeš stvarati razne skupove pomoću 0 i 1 - npr. možeš stvoriti njihov par, {0,1} , označen 2 . I tako dalje... sve do realnih brojeva. A možeš i dalje... 
| Citat: | | jeli stvoren iz čiste slobodoumnosti ili se netko pitao što je komplement univerzalnog skupa ? |
Prije bih rekao da je "univerzalni skup" pojam koji je nastao u pokušaju (aproksimativnog) odgovaranja na pitanje što je komplement praznog skupa. Prazan skup je jedinstven (svi prazni skupovi su jednaki - probaj to dokazati: ), dok univerzalni skup nije. Svaka teorija ima neki svoj univerzalni skup u kojem radi. "Pravi" komplement praznog skupa ne postoji u standardnoj teoriji skupova. "Skup svega" je oksiomoron - to jednostavno nije skup.
| Citat: | | I još nešto,zar je lakše riješiti veliki Fermat-ov problem nego definirati skup ? |
Je li lakše shvatiti Zen ili podići 800kg ? 
Mislim da shvaćaš što hoću reći... to su različite vrste težine. Dokaz FLTa je čisto matematička stvar - definicija skupa je metamatematički problem.
| Citat: | | Gdje nastaju problemi ? |
Pitanje na koje bi se moglo duugo odgovarati (pročitaj npr. početak http://web.math.hr/~veky/em/vjezbe/skupovi.html ), no evo ti ovo za početak. Definicija bi trebala imati prvi općenitiji pojam, i vrsnu razliku, zar ne? E pa, skupovi su (intentionally) toliko općeniti da "prvi općenitiji pojam" baš i ne postoji. Često se skup "definira" kao "kolekcija elemenata kod koje...", kao da je "kolekcija" nešto još općenitije od skupa. Možda, ali "kolekcija" (možda baš zato:! nije matematički pojam - to može služiti samo kao intuitivna definicija. Ne možemo imati i nije matematički pojam - to može služiti samo kao intuitivna definicija. Ne možemo imati i  i :money: - i definirati skup preko ostalih math-pojmova, i definirati sve ostale math-pojmove pomoću skupova. i :money: - i definirati skup preko ostalih math-pojmova, i definirati sve ostale math-pojmove pomoću skupova.
HTH,
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 22:39 sri, 20. 10. 2004 Naslov: Postano: 22:39 sri, 20. 10. 2004 Naslov: |
    |
|
|
[quote]Zato što nije riječ o teoremu koji je naročito važan za teoriju koja se u tom trenutku razvija (elementarna matematika). Možda te zbunila moja uptreba riječi "teorem", koju sam objasnio kad su me prošle godine na ovom forumu optužili da na vježbama "dokazujem teoreme" ( http://degiorgi.math.hr/forum/viewtopic.php?p=9008#9008 ) - ja sam logičar. Meni je teorem ono što se može dokazati. Leme, Korolari, Propozicije, argumentirane Tvrdnje - sve su to teoremi ako imaju dokaz. Unutar neke "akademske" teorije, pojam "Teorem" se obično rezervira za nekoliko centralnih tvrdnji teorije, "Faraone" što bi ti rekao. [/quote]
Jesi li ti u svojim studentskim danima sortirao leme,korolare,propozicije ili si sve jednostavno stavljao pod kapu teorema,dakle dali da u memoriranju prop.,lema,korolara sve jednostavno zaguram u koš teorema i time skratim vrijeme pamćenja ?
Dali da se lišim tih ''činova''-ovo mi je lema,ovo mi je propozicija...
Mislim koliko je nužno primjerice lemu,znati pod ''činom'' leme ?
To je korisno samo recimo na usmenom ispitu gdje ti profesor Šikić primjerice kaže:izreci mi ''zgodnu lemu'' za funkcije pa ti onda automatski djeluješ po memorijsku nahođenju.
[quote]Mda. Ali se svejedno uvijek iznova iznenadim. ;-o[/quote]
Baš bih volio da se barem jednom pozitivno iznenadiš,a ne da si uvijek misliš-o Bože,kakve bljezgarije!? :o)
[quote]Je li lakše shvatiti Zen ili podići 800kg ? ;-D
Mislim da shvaćaš što hoću reći... to su različite vrste težine. Dokaz FLTa je čisto matematička stvar - definicija skupa je metamatematički problem.[/quote]
Pa tko je onda osposobljen za razrješavanje metamatematičkog problema ?
Neka simbioza matematičara i filozofa ?
Filozof matematike ?
Hej(!),ti također rješavaš metamatematički problem,kada si mi rekao da pokušavaš definirati što je broj 3,cool !
[quote]Ne možemo imati i i :money: - i definirati skup preko ostalih math-pojmova, i definirati sve ostale math-pojmove pomoću skupova.[/quote]
Dakle meta-glavolomka oko definiranja skupa nikada neće biti razrješena...
Ovo je dokaz moje math nezrelosti ali doista nisam znao da su svi(figurativno) math pojmovi sigurno naslonjeni na pojam skupa,koji nije definiran,nije li to svojevrsni paradoks vrijedan humora?
Ono,ok,neznamo čvrstinu i materijal od kojeg je izgrađen predmet ali idemo na njega osloniti svo ono staklo što smo napravili. :roll:
Btw,vidi ovo:
A,B skupovi ,A C= B ako vrijedi: Za svaki x@A ; x@B
Zašto fino umjesto znaka ' ; ' ne stoji znak implikacije,jeli uopće taj nimalo intuitivan znak konvencionalan ili nečija(profesor) navika-šarotina? :-s
Opisno govoreći taj znak bi se trebao čitati kako ? :''ujedno i''
Ili to tamo piše slovo ' i ' pa sam te onda opet iznenadio! :doh: :mrgreen:
| Citat: | | Zato što nije riječ o teoremu koji je naročito važan za teoriju koja se u tom trenutku razvija (elementarna matematika). Možda te zbunila moja uptreba riječi "teorem", koju sam objasnio kad su me prošle godine na ovom forumu optužili da na vježbama "dokazujem teoreme" ( http://degiorgi.math.hr/forum/viewtopic.php?p=9008#9008 ) - ja sam logičar. Meni je teorem ono što se može dokazati. Leme, Korolari, Propozicije, argumentirane Tvrdnje - sve su to teoremi ako imaju dokaz. Unutar neke "akademske" teorije, pojam "Teorem" se obično rezervira za nekoliko centralnih tvrdnji teorije, "Faraone" što bi ti rekao. |
Jesi li ti u svojim studentskim danima sortirao leme,korolare,propozicije ili si sve jednostavno stavljao pod kapu teorema,dakle dali da u memoriranju prop.,lema,korolara sve jednostavno zaguram u koš teorema i time skratim vrijeme pamćenja ?
Dali da se lišim tih ''činova''-ovo mi je lema,ovo mi je propozicija...
Mislim koliko je nužno primjerice lemu,znati pod ''činom'' leme ?
To je korisno samo recimo na usmenom ispitu gdje ti profesor Šikić primjerice kaže:izreci mi ''zgodnu lemu'' za funkcije pa ti onda automatski djeluješ po memorijsku nahođenju.
| Citat: | | Mda. Ali se svejedno uvijek iznova iznenadim. ;-o |
Baš bih volio da se barem jednom pozitivno iznenadiš,a ne da si uvijek misliš-o Bože,kakve bljezgarije!? 
| Citat: | Je li lakše shvatiti Zen ili podići 800kg ? 
Mislim da shvaćaš što hoću reći... to su različite vrste težine. Dokaz FLTa je čisto matematička stvar - definicija skupa je metamatematički problem. |
Pa tko je onda osposobljen za razrješavanje metamatematičkog problema ?
Neka simbioza matematičara i filozofa ?
Filozof matematike ?
Hej(!),ti također rješavaš metamatematički problem,kada si mi rekao da pokušavaš definirati što je broj 3,cool !
| Citat: | | Ne možemo imati i i :money: - i definirati skup preko ostalih math-pojmova, i definirati sve ostale math-pojmove pomoću skupova. |
Dakle meta-glavolomka oko definiranja skupa nikada neće biti razrješena...
Ovo je dokaz moje math nezrelosti ali doista nisam znao da su svi(figurativno) math pojmovi sigurno naslonjeni na pojam skupa,koji nije definiran,nije li to svojevrsni paradoks vrijedan humora?
Ono,ok,neznamo čvrstinu i materijal od kojeg je izgrađen predmet ali idemo na njega osloniti svo ono staklo što smo napravili. 
Btw,vidi ovo:
A,B skupovi ,A C= B ako vrijedi: Za svaki x@A ; x@B
Zašto fino umjesto znaka ' ; ' ne stoji znak implikacije,jeli uopće taj nimalo intuitivan znak konvencionalan ili nečija(profesor) navika-šarotina? 
Opisno govoreći taj znak bi se trebao čitati kako ? :''ujedno i''
Ili to tamo piše slovo ' i ' pa sam te onda opet iznenadio!  
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 23:53 sri, 20. 10. 2004 Naslov: Postano: 23:53 sri, 20. 10. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"][quote]Zato što nije riječ o teoremu koji je naročito važan za teoriju koja se u tom trenutku razvija (elementarna matematika). Možda te zbunila moja uptreba riječi "teorem", koju sam objasnio kad su me prošle godine na ovom forumu optužili da na vježbama "dokazujem teoreme" ( http://degiorgi.math.hr/forum/viewtopic.php?p=9008#9008 ) - ja sam logičar. Meni je teorem ono što se može dokazati. Leme, Korolari, Propozicije, argumentirane Tvrdnje - sve su to teoremi ako imaju dokaz. Unutar neke "akademske" teorije, pojam "Teorem" se obično rezervira za nekoliko centralnih tvrdnji teorije, "Faraone" što bi ti rekao. [/quote]
Jesi li ti u svojim studentskim danima sortirao leme,korolare,propozicije ili si sve jednostavno stavljao pod kapu teorema,dakle dali da u memoriranju prop.,lema,korolara sve jednostavno zaguram u koš teorema i time skratim vrijeme pamćenja ?
Dali da se lišim tih ''činova''-ovo mi je lema,ovo mi je propozicija...[/quote]
Ako ti stvarno to predstavlja neku dodatnu teškoću, nećeš puno konkretnoga izgubiti lišiš li se toga. No izgubit ćeš na apstraktnom planu, jer će stradati tvoj osjećaj za bitno i nebitno, te ćeš teže razlikovati da je nešto "Faraon", nešto drugo samo tehnička Lema da bi se Faraona lakše dokazalo, a nešto treće samo lagani Faraonov korolar. Za logiku je to isto, ali za ljudsku psihologiju i ne mora biti.
[quote]Mislim koliko je nužno primjerice lemu,znati pod ''činom'' leme ?
To je korisno samo recimo na usmenom ispitu gdje ti profesor Šikić primjerice kaže:izreci mi ''zgodnu lemu'' za funkcije pa ti onda automatski djeluješ po memorijsku nahođenju.[/quote]
Naravno. Mislim da sam već pisao o tome po Forumu... na mom usmenom iz MA4, prvo pitanje mi je bilo Poincareova lema. Trebalo mi je više od jedne minute da se sjetim što je dovvaga Poincareova lema, i sigurno manje od minute da je dokažem. :-)
[quote][quote]Mda. Ali se svejedno uvijek iznova iznenadim. ;-o[/quote]
Baš bih volio da se barem jednom pozitivno iznenadiš,a ne da si uvijek misliš-o Bože,kakve bljezgarije!? :o)[/quote]
Pa bude i toga povremeno. ;-)
[quote][quote]Je li lakše shvatiti Zen ili podići 800kg ? ;-D
Mislim da shvaćaš što hoću reći... to su različite vrste težine. Dokaz FLTa je čisto matematička stvar - definicija skupa je metamatematički problem.[/quote]
Pa tko je onda osposobljen za razrješavanje metamatematičkog problema ?
Neka simbioza matematičara i filozofa ?
Filozof matematike ?[/quote]
Na primjer.
[quote]Hej(!),ti također rješavaš metamatematički problem,kada si mi rekao da pokušavaš definirati što je broj 3,cool ![/quote]
Ja inače volim metamatematiku, ali ovo i nije toliki argument. Naime, broj 3 je samo specijalan skup (za mene), inače jednak {0,1,2} (definicije 0 , 1 i 2 imaš gore; ). Kao i sve ostalo... no _općenit pojam skupa_ je ono što ne definiram (matematički).
[quote][quote]Ne možemo imati i :ofca: i :money: - i definirati skup preko ostalih math-pojmova, i definirati sve ostale math-pojmove pomoću skupova.[/quote]
Dakle meta-glavolomka oko definiranja skupa nikada neće biti razrješena...[/quote]
Mah. Kao ni oko bilo kojeg filozofskog pitanja. :-)
Što ne znači da ne možemo imati sasvim zadovoljavajuće "radne" definicije - jednu sam naveo gore, a imaš je i na onoj stranici čiji link navedoh.
[quote]Ovo je dokaz moje math nezrelosti ali doista nisam znao da su svi(figurativno) math pojmovi sigurno naslonjeni na pojam skupa,koji nije definiran,nije li to svojevrsni paradoks vrijedan humora?[/quote]
Nije. To je sasvim logična činjenica. Razmisli malo - svaki pojam je definiran pomoću nekih drugih pojmova, oni opet preko nekih trećih, itd. . Otfuravši to do krajnosti (kako mathematičari obično vole raditi; ), relativno lako se vidi da imaš samo tri mogućnosti:
1. Ovo gore: jedan koncept, od kojeg počinješ, i na kojeg možeš svesti sve ostale.
2. Cirkularne definicije: Negdje imaš pojam A definiran pomoću pojma B , a pojam B u svojoj definiciji koristi pojam A . Ili jednostavno, definiraš pojam A pomoću samog sebe.
3. Beskonačno silazne definicije: beskonačan niz pojmova, svaki od njih "jednostavniji" od onog prethodnog, kojeg definira: A1 je definirano pomoću A2 , A2 pomoću A3 , A3 pomoću A4 i tako u beskonačnost.
Meni se 2. i 3. čine totalno neprihvatljivima. Tebi?
(Ili misliš da postoji 4. mogućnost?)
[quote]Ono,ok,neznamo čvrstinu i materijal od kojeg je izgrađen predmet ali idemo na njega osloniti svo ono staklo što smo napravili. :roll:[/quote]
Znamo. Prazan skup se sastoji od ničega. ;-)
[quote]Btw,vidi ovo:
A,B skupovi ,A C= B ako vrijedi: Za svaki x@A ; x@B
Zašto fino umjesto znaka ' ; ' ne stoji znak implikacije,[/quote]
Zato što se tad formula ne bi mogla parsirati. Pokušaj.
x@A je očito jedna potformula. x@B je druga. Ako ih povežeš znakom implikacije (logički veznik), dobit ćeš x@A=>x@B . I to je ok.
No što sad dodati toj formuli da bi ona postala ovo gore? "Za svaki"? Očito, nedostaje "za svaki _što_?". Naravno, nama je jasno, budući da je jedina varijabla koja se ovdje pojavljuje x , da to znači "za svaki x ". No logika voli biti univerzalna koliko već može. Što da smo imali više varijabli - na koju bi se tad odnosio kvantifikator?
Zato je jednostavnije "za svaki x " nazvati kvantifikatorom, a ono što slijedi nakon toga shvatiti kao posebnu formulu. No u skupovnom pogledu na stvari, prirodno je umjesto "neograničene" kvantifikacije "za svaki x , što god x bio", ograničiti se na elemente nekog skupa - "za svaki x@S , vrijedi nešto". Tako treba shvatiti i gornju formulu. Parsirano po potformulama, to je [latex](\forall x\in A)(x\in B)[/latex].
Sad je samo stvar u tome da se čovjeku ne da pisati zagrade, pa da bi odvojio te dvije "polovice" formule, ne stavlja svaku u zagradu, nego ih odvaja točkazarezom.
[quote]jeli uopće taj nimalo intuitivan znak konvencionalan ili nečija(profesor) navika-šarotina? :-s[/quote]
Prilično je uobičajen - doduše, češći je kod egzistencijalnog kvantifikatora, gdje ima prirodno čitanje "takav da": npr. [latex](\exists x\in A)(x\in B)[/latex], odnosno [latex]\exists x\in A;\;x\in B[/latex] se prirodno čita kao "postoji iks iz a takav da je iks iz be" .
(i kad smo već kod toga, kao takav je meni puno prirodniji i lakši za napisati:-) nego onaj šikićevski 'obrnuti psi'. No, svakom njegova notacija...: )
[quote]Opisno govoreći taj znak bi se trebao čitati kako ? :''ujedno i''[/quote]
Jednostavno "vrijedi". Ili samo "," (zarez: ). "Za svaki iks iz a , iks je iz be."
Ovo "ujedno i" je pokušaj overgeneralizacije činjenice koju ovdje vidiš, a to je da se u x@B i u x@A pojavljuje ista relacija - biti element. To ne mora biti tako. Da je npr. pisalo "x !@ B" ('x nije element od B'), uvjeren sam da ga ne bi čitao "ujedno i". ;->
[quote]Ili to tamo piše slovo ' i ' pa sam te onda opet iznenadio! :doh: :mrgreen:[/quote]
Sumnjam. "i" se obično rezervira za konjunkciju, što ovdje nikako nije. Prije implikacija, ako baš moraš to shvatiti kao logički veznik. No, rekoh, tad 'x' moraš napisati dvaput. :shock: ;-)
| Vincent Van Ear (napisa): | | Citat: | | Zato što nije riječ o teoremu koji je naročito važan za teoriju koja se u tom trenutku razvija (elementarna matematika). Možda te zbunila moja uptreba riječi "teorem", koju sam objasnio kad su me prošle godine na ovom forumu optužili da na vježbama "dokazujem teoreme" ( http://degiorgi.math.hr/forum/viewtopic.php?p=9008#9008 ) - ja sam logičar. Meni je teorem ono što se može dokazati. Leme, Korolari, Propozicije, argumentirane Tvrdnje - sve su to teoremi ako imaju dokaz. Unutar neke "akademske" teorije, pojam "Teorem" se obično rezervira za nekoliko centralnih tvrdnji teorije, "Faraone" što bi ti rekao. |
Jesi li ti u svojim studentskim danima sortirao leme,korolare,propozicije ili si sve jednostavno stavljao pod kapu teorema,dakle dali da u memoriranju prop.,lema,korolara sve jednostavno zaguram u koš teorema i time skratim vrijeme pamćenja ?
Dali da se lišim tih ''činova''-ovo mi je lema,ovo mi je propozicija... |
Ako ti stvarno to predstavlja neku dodatnu teškoću, nećeš puno konkretnoga izgubiti lišiš li se toga. No izgubit ćeš na apstraktnom planu, jer će stradati tvoj osjećaj za bitno i nebitno, te ćeš teže razlikovati da je nešto "Faraon", nešto drugo samo tehnička Lema da bi se Faraona lakše dokazalo, a nešto treće samo lagani Faraonov korolar. Za logiku je to isto, ali za ljudsku psihologiju i ne mora biti.
| Citat: | Mislim koliko je nužno primjerice lemu,znati pod ''činom'' leme ?
To je korisno samo recimo na usmenom ispitu gdje ti profesor Šikić primjerice kaže:izreci mi ''zgodnu lemu'' za funkcije pa ti onda automatski djeluješ po memorijsku nahođenju. |
Naravno. Mislim da sam već pisao o tome po Forumu... na mom usmenom iz MA4, prvo pitanje mi je bilo Poincareova lema. Trebalo mi je više od jedne minute da se sjetim što je dovvaga Poincareova lema, i sigurno manje od minute da je dokažem. 
| Citat: | | Citat: | | Mda. Ali se svejedno uvijek iznova iznenadim. ;-o |
Baš bih volio da se barem jednom pozitivno iznenadiš,a ne da si uvijek misliš-o Bože,kakve bljezgarije!?  |
Pa bude i toga povremeno. 
| Citat: | | Citat: | Je li lakše shvatiti Zen ili podići 800kg ? 
Mislim da shvaćaš što hoću reći... to su različite vrste težine. Dokaz FLTa je čisto matematička stvar - definicija skupa je metamatematički problem. |
Pa tko je onda osposobljen za razrješavanje metamatematičkog problema ?
Neka simbioza matematičara i filozofa ?
Filozof matematike ? |
Na primjer.
| Citat: | | Hej(!),ti također rješavaš metamatematički problem,kada si mi rekao da pokušavaš definirati što je broj 3,cool ! |
Ja inače volim metamatematiku, ali ovo i nije toliki argument. Naime, broj 3 je samo specijalan skup (za mene), inače jednak {0,1,2} (definicije 0 , 1 i 2 imaš gore; ). Kao i sve ostalo... no _općenit pojam skupa_ je ono što ne definiram (matematički).
| Citat: | | Citat: | | Ne možemo imati i :ofca: i :money: - i definirati skup preko ostalih math-pojmova, i definirati sve ostale math-pojmove pomoću skupova. |
Dakle meta-glavolomka oko definiranja skupa nikada neće biti razrješena... |
Mah. Kao ni oko bilo kojeg filozofskog pitanja. 
Što ne znači da ne možemo imati sasvim zadovoljavajuće "radne" definicije - jednu sam naveo gore, a imaš je i na onoj stranici čiji link navedoh.
| Citat: | | Ovo je dokaz moje math nezrelosti ali doista nisam znao da su svi(figurativno) math pojmovi sigurno naslonjeni na pojam skupa,koji nije definiran,nije li to svojevrsni paradoks vrijedan humora? |
Nije. To je sasvim logična činjenica. Razmisli malo - svaki pojam je definiran pomoću nekih drugih pojmova, oni opet preko nekih trećih, itd. . Otfuravši to do krajnosti (kako mathematičari obično vole raditi; ), relativno lako se vidi da imaš samo tri mogućnosti:
1. Ovo gore: jedan koncept, od kojeg počinješ, i na kojeg možeš svesti sve ostale.
2. Cirkularne definicije: Negdje imaš pojam A definiran pomoću pojma B , a pojam B u svojoj definiciji koristi pojam A . Ili jednostavno, definiraš pojam A pomoću samog sebe.
3. Beskonačno silazne definicije: beskonačan niz pojmova, svaki od njih "jednostavniji" od onog prethodnog, kojeg definira: A1 je definirano pomoću A2 , A2 pomoću A3 , A3 pomoću A4 i tako u beskonačnost.
Meni se 2. i 3. čine totalno neprihvatljivima. Tebi?
(Ili misliš da postoji 4. mogućnost?)
| Citat: | Ono,ok,neznamo čvrstinu i materijal od kojeg je izgrađen predmet ali idemo na njega osloniti svo ono staklo što smo napravili.  |
Znamo. Prazan skup se sastoji od ničega. 
| Citat: | Btw,vidi ovo:
A,B skupovi ,A C= B ako vrijedi: Za svaki x@A ; x@B
Zašto fino umjesto znaka ' ; ' ne stoji znak implikacije, |
Zato što se tad formula ne bi mogla parsirati. Pokušaj.
x@A je očito jedna potformula. x@B je druga. Ako ih povežeš znakom implikacije (logički veznik), dobit ćeš x@A⇒x@B . I to je ok.
No što sad dodati toj formuli da bi ona postala ovo gore? "Za svaki"? Očito, nedostaje "za svaki _što_?". Naravno, nama je jasno, budući da je jedina varijabla koja se ovdje pojavljuje x , da to znači "za svaki x ". No logika voli biti univerzalna koliko već može. Što da smo imali više varijabli - na koju bi se tad odnosio kvantifikator?
Zato je jednostavnije "za svaki x " nazvati kvantifikatorom, a ono što slijedi nakon toga shvatiti kao posebnu formulu. No u skupovnom pogledu na stvari, prirodno je umjesto "neograničene" kvantifikacije "za svaki x , što god x bio", ograničiti se na elemente nekog skupa - "za svaki x@S , vrijedi nešto". Tako treba shvatiti i gornju formulu. Parsirano po potformulama, to je 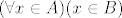 . .
Sad je samo stvar u tome da se čovjeku ne da pisati zagrade, pa da bi odvojio te dvije "polovice" formule, ne stavlja svaku u zagradu, nego ih odvaja točkazarezom.
| Citat: | jeli uopće taj nimalo intuitivan znak konvencionalan ili nečija(profesor) navika-šarotina?  |
Prilično je uobičajen - doduše, češći je kod egzistencijalnog kvantifikatora, gdje ima prirodno čitanje "takav da": npr. 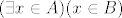 , odnosno , odnosno 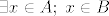 se prirodno čita kao "postoji iks iz a takav da je iks iz be" . se prirodno čita kao "postoji iks iz a takav da je iks iz be" .
(i kad smo već kod toga, kao takav je meni puno prirodniji i lakši za napisati:-) nego onaj šikićevski 'obrnuti psi'. No, svakom njegova notacija...: )
| Citat: | | Opisno govoreći taj znak bi se trebao čitati kako ? :''ujedno i'' |
Jednostavno "vrijedi". Ili samo "," (zarez: ). "Za svaki iks iz a , iks je iz be."
Ovo "ujedno i" je pokušaj overgeneralizacije činjenice koju ovdje vidiš, a to je da se u x@B i u x@A pojavljuje ista relacija - biti element. To ne mora biti tako. Da je npr. pisalo "x !@ B" ('x nije element od B'), uvjeren sam da ga ne bi čitao "ujedno i". ;→
| Citat: | Ili to tamo piše slovo ' i ' pa sam te onda opet iznenadio!   |
Sumnjam. "i" se obično rezervira za konjunkciju, što ovdje nikako nije. Prije implikacija, ako baš moraš to shvatiti kao logički veznik. No, rekoh, tad 'x' moraš napisati dvaput.  
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 11:01 čet, 21. 10. 2004 Naslov: Postano: 11:01 čet, 21. 10. 2004 Naslov: |
    |
|
|
[quote]Ako ti stvarno to predstavlja neku dodatnu teškoću, nećeš puno konkretnoga izgubiti lišiš li se toga. No izgubit ćeš na apstraktnom planu, jer će stradati tvoj osjećaj za bitno i nebitno, te ćeš teže razlikovati da je nešto "Faraon", nešto drugo samo tehnička Lema da bi se Faraona lakše dokazalo, a nešto treće samo lagani Faraonov korolar. Za logiku je to isto, ali za ljudsku psihologiju i ne mora biti.[/quote]
Ok,onda ću ostaviti kako je.
Ma ne,nije mi teškoća,dapače,ovako je cijela stvar šarenija i nekako(nazovi) djetinjastija(ali ipak svrsishodna). ;)
[quote]Meni se 2. i 3. čine totalno neprihvatljivima. Tebi?
(Ili misliš da postoji 4. mogućnost?)[/quote]
Da,fantastično je to da se pomoću samo jednog jedincatog nedefiniranog može definirati sve ostalo,onda je to doista prihvatljivo.
Hej dakle imamo Boga kojega neznamo definirati ali sve što postoji naslanjamo na njega,a kako on nije materijalan onda je sastavljen od ničega baš kao i prazan skup pa je komplement svemira Bog! :mrgreen:
| Citat: | | Ako ti stvarno to predstavlja neku dodatnu teškoću, nećeš puno konkretnoga izgubiti lišiš li se toga. No izgubit ćeš na apstraktnom planu, jer će stradati tvoj osjećaj za bitno i nebitno, te ćeš teže razlikovati da je nešto "Faraon", nešto drugo samo tehnička Lema da bi se Faraona lakše dokazalo, a nešto treće samo lagani Faraonov korolar. Za logiku je to isto, ali za ljudsku psihologiju i ne mora biti. |
Ok,onda ću ostaviti kako je.
Ma ne,nije mi teškoća,dapače,ovako je cijela stvar šarenija i nekako(nazovi) djetinjastija(ali ipak svrsishodna). 
| Citat: | Meni se 2. i 3. čine totalno neprihvatljivima. Tebi?
(Ili misliš da postoji 4. mogućnost?) |
Da,fantastično je to da se pomoću samo jednog jedincatog nedefiniranog može definirati sve ostalo,onda je to doista prihvatljivo.
Hej dakle imamo Boga kojega neznamo definirati ali sve što postoji naslanjamo na njega,a kako on nije materijalan onda je sastavljen od ničega baš kao i prazan skup pa je komplement svemira Bog! 
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
|





