| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 15:58 sub, 13. 11. 2004 Naslov: Propozicija ''o presjeku skupovnih razlika'' Postano: 15:58 sub, 13. 11. 2004 Naslov: Propozicija ''o presjeku skupovnih razlika'' |
    |
|
|
[color=green]Propozicija:
Pretpostavke:A,B C= U
Doprinos: (A\B)n(B\A)=0[/color]
[b]Dokaz:[/b]
Pretpostavi se suprotno i dođe se(sasvim očekivano) do kontradikcije.
Što kada bih išao raspisivati dokaz po definiciji ''biti podskup'',ajmo vidjeti :
Definicija jednakost skupova Tvrdnja iz teorema => Tvrdnja1:(A\B)n(B\A) C= 0 i Tvrdnja2:0 C= (A\B)n(B\A)
Tvrdnja1:dokaz:
Prz. x@(A\B)n(B\A)
Def.presjeka=>x@A\B i x@B\A
Def.skupovne razlike=>x@A i x!@B i x@B i x!@A ,što je očito kontradikcija jer x ne može biti iz A i iz neA baš kao što ne može biti iz B i neB.
Samo,to je kontradikcija s čime ?
Idem li odozdo prema gore u dokazu,sve sam obavljao po definicijama,jedina ''radnja'' koja nema pokrića jest što sam iz skupa (A\B)n(B\A) uzeo element,a nisam znao(stoga sam pretpostavio nešto što nisam smio odnosno dokaz ne trpi pretpostavke) jeli taj skup uopće ima svojstvo da posjeduje elemente odnosno da je neprazan.
Očito je kontradikcija u tome,jeli tako ?
Zaključak:skup (A\B)n(B\A) je prazan _skup_.
Svaki skup ima to svojstvo da je podskup samoga sebe(jamac je jedna propozicija),ili smo mogli reći(po jednom teoremu)da je prazan skup podskup _svakog_ skupa, pa prema tome vrijedi da je (A\B)n(B\A)=0 C= 0 [b]CUBE;)[/b]
Tvrdnja2:dokaz:
Trivijalno,prazan skup(po jednom teoremu) je podskup svakoga skupa pa specijalno i skupa (A\B)n(B\A) [b]CUBE;)[/b]
PS:
Ovo će djelovati glupo ali kada bi me netko nadobudan pitao da mu dokažem da je objekt (A\B)n(B\A) skup bili bilo dovoljno da mu kažem ovako:
A\B je po definiciji skup kao i B\A ,a presjek skupova po definiciji je skup.
Propozicija:
Pretpostavke:A,B C= U
Doprinos: (A\B)n(B\A)=0
Dokaz:
Pretpostavi se suprotno i dođe se(sasvim očekivano) do kontradikcije.
Što kada bih išao raspisivati dokaz po definiciji ''biti podskup'',ajmo vidjeti :
Definicija jednakost skupova Tvrdnja iz teorema => Tvrdnja1:(A\B)n(B\A) C= 0 i Tvrdnja2:0 C= (A\B)n(B\A)
Tvrdnja1:dokaz:
Prz. x@(A\B)n(B\A)
Def.presjeka=>x@A\B i x@B\A
Def.skupovne razlike=>x@A i x!@B i x@B i x!@A ,što je očito kontradikcija jer x ne može biti iz A i iz neA baš kao što ne može biti iz B i neB.
Samo,to je kontradikcija s čime ?
Idem li odozdo prema gore u dokazu,sve sam obavljao po definicijama,jedina ''radnja'' koja nema pokrića jest što sam iz skupa (A\B)n(B\A) uzeo element,a nisam znao(stoga sam pretpostavio nešto što nisam smio odnosno dokaz ne trpi pretpostavke) jeli taj skup uopće ima svojstvo da posjeduje elemente odnosno da je neprazan.
Očito je kontradikcija u tome,jeli tako ?
Zaključak:skup (A\B)n(B\A) je prazan _skup_.
Svaki skup ima to svojstvo da je podskup samoga sebe(jamac je jedna propozicija),ili smo mogli reći(po jednom teoremu)da je prazan skup podskup _svakog_ skupa, pa prema tome vrijedi da je (A\B)n(B\A)=0 C= 0 CUBE;)
Tvrdnja2:dokaz:
Trivijalno,prazan skup(po jednom teoremu) je podskup svakoga skupa pa specijalno i skupa (A\B)n(B\A) CUBE;)
PS:
Ovo će djelovati glupo ali kada bi me netko nadobudan pitao da mu dokažem da je objekt (A\B)n(B\A) skup bili bilo dovoljno da mu kažem ovako:
A\B je po definiciji skup kao i B\A ,a presjek skupova po definiciji je skup.
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 22:55 sub, 13. 11. 2004 Naslov: Re: Propozicija ''o presjeku skupovnih razlika'' Postano: 22:55 sub, 13. 11. 2004 Naslov: Re: Propozicija ''o presjeku skupovnih razlika'' |
    |
|
|
[quote="mdoko"]
Sto ustvari hoce reci da za svaki skup x postoji skup y takav da je z element od y ako i samo ako je z element od x i ako vrijedi [latex]\varphi(z)[/latex].
Odnosno kaze da je [latex] \{ z | z \in x \land \varphi(z) \}[/latex] skup.[/quote]
Konkretno, ovdje je (za skup (A\B)n(B\A) ) bitno uočiti da je presjek, i razlika, dva skupa sigurno podskup prvog od njih. Dakle, prvo po gornjem aksiomu,
za x:=A & fi(z):<=>x(!@)B ,
slijedi da je y=A\B skup. (Analogno B\A ). Sada ponovo po gornjem aksiomu,
za x:=A\B & fi(z):<=>x@B\A ,
slijedi da je y=(A\B)n(B\A) skup.
(@Vincent: Inače, ako ne odgovorim na neki tvoj post u kojem samo iznosiš svoja razmišljanja, to znači nemam ništa krupno za prigovoriti, odnosno da su tvrdnje iznesene u njemu uglavnom prihvatljive. To si već shvatio, zar ne?: )
| mdoko (napisa): |
Sto ustvari hoce reci da za svaki skup x postoji skup y takav da je z element od y ako i samo ako je z element od x i ako vrijedi 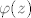 . .
Odnosno kaze da je 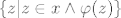 skup. skup. |
Konkretno, ovdje je (za skup (A\B)n(B\A) ) bitno uočiti da je presjek, i razlika, dva skupa sigurno podskup prvog od njih. Dakle, prvo po gornjem aksiomu,
za x:=A & fi(z):⇔x(!@)B ,
slijedi da je y=A\B skup. (Analogno B\A ). Sada ponovo po gornjem aksiomu,
za x:=A\B & fi(z):⇔x@B\A ,
slijedi da je y=(A\B)n(B\A) skup.
(@Vincent: Inače, ako ne odgovorim na neki tvoj post u kojem samo iznosiš svoja razmišljanja, to znači nemam ništa krupno za prigovoriti, odnosno da su tvrdnje iznesene u njemu uglavnom prihvatljive. To si već shvatio, zar ne?: )
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 2:18 ned, 14. 11. 2004 Naslov: Postano: 2:18 ned, 14. 11. 2004 Naslov: |
    |
|
|
[quote] Axpostojiy(Az(z@y<=>(z@x i fi(z))))gdje je bilo koja formula ZF teorije.
Sto ustvari hoce reci da za svaki skup x postoji skup y takav da je z element od y ako i samo ako je z element od x i ako vrijedi .
Odnosno kaze da je skup.
Konkretno, ovdje je (za skup (A\B)n(B\A) ) bitno uočiti da je presjek, i razlika, dva skupa sigurno podskup prvog od njih. Dakle, prvo po gornjem aksiomu,
za x:=A & fi(z):<=>x(!@)B ,
slijedi da je y=A\B skup. (Analogno B\A ). Sada ponovo po gornjem aksiomu,
za x:=A\B & fi(z):<=>x@B\A ,
slijedi da je y=(A\B)n(B\A) skup.[/quote]
Mlako sam to shvatio :grrr: ,mada sam probao:
'Za svaki skup postoji skup...'
Dakle,imajući jedan skup imamo još jedan uz određene zahtjeve za elemente tog drugog skupa,odnosno objekt oblika
je skup ako su njegovi elementi iz _skupa_ x(vjerujem da je on pretpostavljen) i vrijedi _formula u ZF_(?).
Pretpostavljam da je A skup(da je to skup nekako znam,pardon,pretpostavljam,vjerojatno to smijem pretpostaviti jer promatrajući objekt (A\B)n(B\A) zaključujem da su skupovi A i B njegove ''najmanje građevne jedinice'' :crazy: ) i označim ga(malim slovom,ja mislio da skupove označavamo striktno velikim slovima,a onda se uvjerih da smo relacije označavali malim slovom 'ro' pa vidim i ovdje u ZF(štogod ta kratica krila,prema sadržaju bih rekao-Znanstvena Fantastika :mrgreen: ) se skupovi označavaju malim slovom) sa x :
x:=A ,i sad,tu su nastali problemi jer ne shvaćam simboliku ' :<=> ',pa sam ja to shvatio kao:formulu ZF teorije imamo ako i samo ako x nije iz skupa B,hm,nebi li trebalo pisati ako z nije iz B tako da se element x ne miješa sa skupom x(mada si to vjerojatno izbjegao supstitucijom x:=A).
Uglavnom imamo skup čiji su elementi iz skupa A(jer je A\B C= A ) i oni nisu u B pa je A\B skup.
Analogno sa B\A.
:-k
[quote](@Vincent: Inače, ako ne odgovorim na neki tvoj post u kojem samo iznosiš svoja razmišljanja, to znači nemam ništa _krupno_ za prigovoriti, odnosno da su tvrdnje iznesene u njemu _uglavnom_ prihvatljive.[/quote]
Kako je to lijep osjećaj kada vidim da nisam nigdje(krupno v uglavnom) falšao jer ipak si Ti :mrgreen: skenirao.
:banana:
[quote] To si već shvatio, zar ne?: )[/quote]
Iskreno-ne!
Mislio sam da si ljut što sam ti uzalud potrošio točno (sqrt3)^2 fotokopirna papira. :mrgreen:
of course-a joke,I owe you one! :bow:
| Citat: | Axpostojiy(Az(z@y⇔(z@x i fi(z))))gdje je bilo koja formula ZF teorije.
Sto ustvari hoce reci da za svaki skup x postoji skup y takav da je z element od y ako i samo ako je z element od x i ako vrijedi .
Odnosno kaze da je skup.
Konkretno, ovdje je (za skup (A\B)n(B\A) ) bitno uočiti da je presjek, i razlika, dva skupa sigurno podskup prvog od njih. Dakle, prvo po gornjem aksiomu,
za x:=A & fi(z):⇔x(!@)B ,
slijedi da je y=A\B skup. (Analogno B\A ). Sada ponovo po gornjem aksiomu,
za x:=A\B & fi(z):⇔x@B\A ,
slijedi da je y=(A\B)n(B\A) skup. |
Mlako sam to shvatio  ,mada sam probao: ,mada sam probao:
'Za svaki skup postoji skup...'
Dakle,imajući jedan skup imamo još jedan uz određene zahtjeve za elemente tog drugog skupa,odnosno objekt oblika
je skup ako su njegovi elementi iz _skupa_ x(vjerujem da je on pretpostavljen) i vrijedi _formula u ZF_(?).
Pretpostavljam da je A skup(da je to skup nekako znam,pardon,pretpostavljam,vjerojatno to smijem pretpostaviti jer promatrajući objekt (A\B)n(B\A) zaključujem da su skupovi A i B njegove ''najmanje građevne jedinice''  ) i označim ga(malim slovom,ja mislio da skupove označavamo striktno velikim slovima,a onda se uvjerih da smo relacije označavali malim slovom 'ro' pa vidim i ovdje u ZF(štogod ta kratica krila,prema sadržaju bih rekao-Znanstvena Fantastika ) i označim ga(malim slovom,ja mislio da skupove označavamo striktno velikim slovima,a onda se uvjerih da smo relacije označavali malim slovom 'ro' pa vidim i ovdje u ZF(štogod ta kratica krila,prema sadržaju bih rekao-Znanstvena Fantastika  ) se skupovi označavaju malim slovom) sa x : ) se skupovi označavaju malim slovom) sa x :
x:=A ,i sad,tu su nastali problemi jer ne shvaćam simboliku ' :⇔ ',pa sam ja to shvatio kao:formulu ZF teorije imamo ako i samo ako x nije iz skupa B,hm,nebi li trebalo pisati ako z nije iz B tako da se element x ne miješa sa skupom x(mada si to vjerojatno izbjegao supstitucijom x:=A).
Uglavnom imamo skup čiji su elementi iz skupa A(jer je A\B C= A ) i oni nisu u B pa je A\B skup.
Analogno sa B\A.

| Citat: | | (@Vincent: Inače, ako ne odgovorim na neki tvoj post u kojem samo iznosiš svoja razmišljanja, to znači nemam ništa _krupno_ za prigovoriti, odnosno da su tvrdnje iznesene u njemu _uglavnom_ prihvatljive. |
Kako je to lijep osjećaj kada vidim da nisam nigdje(krupno v uglavnom) falšao jer ipak si Ti  skenirao. skenirao.

| Citat: | | To si već shvatio, zar ne?: ) |
Iskreno-ne!
Mislio sam da si ljut što sam ti uzalud potrošio točno (sqrt3)^2 fotokopirna papira. 
of course-a joke,I owe you one! 
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 3:57 ned, 14. 11. 2004 Naslov: Postano: 3:57 ned, 14. 11. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"]
Mlako sam to shvatio :grrr: ,mada sam probao:[/quote]
Pa imaš vremena... TS je tek na trećoj/četvrtoj godini... :-)
[quote]Dakle,imajući jedan skup imamo još jedan uz određene zahtjeve za elemente tog drugog skupa,odnosno objekt oblika
je skup ako su njegovi elementi iz _skupa_ x(vjerujem da je on pretpostavljen) i vrijedi _formula u ZF_(?).[/quote]
"Formula" u ovom slučaju ima "slobodnu varijablu" z , što znači da "vrijedi" (ili ne vrijedi) ne apsolutno (kao sud), već vrijedi (ili ne vrijedi) _za neki objekt_ koji se uvrštava umjesto varijable z . Recimo, formula fi s jednom slobodnom varijablom, zadana s fi(z):<=>z@{1,2,3} vrijedi za 1 , ali ne za 4 .
[quote]Pretpostavljam da je A skup(da je to skup nekako znam,pardon,pretpostavljam,vjerojatno to smijem pretpostaviti jer promatrajući objekt (A\B)n(B\A) zaključujem da su skupovi A i B njegove ''najmanje građevne jedinice'' :crazy: )[/quote]
Ama što će ti sve to? Pa samo pogledaj što piše u pretpostavkama propozicije. A i B su podskupovi od U . Dakle, skupovi.
[quote] i označim ga(malim slovom,ja mislio da skupove označavamo striktno velikim slovima,[/quote]
Dok ste još u "urelement"-mentalitetu, u kojem se math-objekti dijele na skupove i ne-skupove, dobro je različito ih označavati.
[quote]a onda se uvjerih da smo relacije označavali malim slovom 'ro' pa vidim i ovdje u ZF(štogod ta kratica krila,prema sadržaju bih rekao-Znanstvena Fantastika :mrgreen: )[/quote]
Fantastika, ali ne baš znanstvena. ;-)
Zermelo-Fraenkelova standardna teorija skupova.
http://www.cs.bilkent.edu.tr/~akman/jour-papers/air/node5.html
[quote] se skupovi označavaju malim slovom) sa x :[/quote]
Stvar je u tome da, u ZF, _svi_ math-objekti su skupovi. Pa onda nema smisla svjesno se odreći polovice slovâ...
Osim toga, većina math-teorijâ primarne objekte koje proučava označava malim slovima: analiza realne brojeve, linearna algebra vektore... teorija skupova primarno proučava ('đenje!: ) skupove.
[quote]x:=A ,i sad,tu su nastali problemi jer ne shvaćam simboliku ' :<=> ',pa sam ja to shvatio kao:formulu ZF teorije imamo ako i samo ako x nije iz skupa B,[/quote]
Jednostavno, tako definiram formulu koja mi "ovisi" o z . Slično kao što funkciju koja mi "ovisi" o x definiram s npr. f(x):=3x+1 .
Za brojeve i izraze to je = , jednakost. Za formule, to je logička ekvivalencija, <=> .
[quote]hm,nebi li trebalo pisati ako z nije iz B[/quote]
Bi. :oops: Mah, cijelo vrijeme u elementarnoj označavamo "tipični element skupa" s x , pa sam to prenio i ovdje. :-/
[quote] tako da se element x ne miješa sa skupom x(mada si to vjerojatno izbjegao supstitucijom x:=A).[/quote]
Što se toga tiče je ok (iako nije u skladu s nečim što se zove zvučnim imenom Konvencija o varijablama, ali to je ionako uglavnom estetska stvar), ali nije ok jer formula nije dobro opisana. Umjesto fi(z) na lijevoj strani bi trebalo ići fi(x) .
(Zapravo, striktno logički, to _jest_ svejedno. Varijable se, između ostalog da bi ih se imalo beskonačno mnogo i izbjegla konačnost abecede, označavaju redom s v0,v1,v2,.... . Tako da, kad kažemo da formula ima jednu slobodnu varijablu, podrazumijeva se da je to v0 . Ono što piše u zagradama je tada samo psihološka pomoć - ili, u ovom slučaju, odmoć. [:-)] )
| Vincent Van Ear (napisa): |
Mlako sam to shvatio  ,mada sam probao: ,mada sam probao: |
Pa imaš vremena... TS je tek na trećoj/četvrtoj godini... 
| Citat: | Dakle,imajući jedan skup imamo još jedan uz određene zahtjeve za elemente tog drugog skupa,odnosno objekt oblika
je skup ako su njegovi elementi iz _skupa_ x(vjerujem da je on pretpostavljen) i vrijedi _formula u ZF_(?). |
"Formula" u ovom slučaju ima "slobodnu varijablu" z , što znači da "vrijedi" (ili ne vrijedi) ne apsolutno (kao sud), već vrijedi (ili ne vrijedi) _za neki objekt_ koji se uvrštava umjesto varijable z . Recimo, formula fi s jednom slobodnom varijablom, zadana s fi(z):⇔z@{1,2,3} vrijedi za 1 , ali ne za 4 .
| Citat: | Pretpostavljam da je A skup(da je to skup nekako znam,pardon,pretpostavljam,vjerojatno to smijem pretpostaviti jer promatrajući objekt (A\B)n(B\A) zaključujem da su skupovi A i B njegove ''najmanje građevne jedinice''  ) ) |
Ama što će ti sve to? Pa samo pogledaj što piše u pretpostavkama propozicije. A i B su podskupovi od U . Dakle, skupovi.
| Citat: | | i označim ga(malim slovom,ja mislio da skupove označavamo striktno velikim slovima, |
Dok ste još u "urelement"-mentalitetu, u kojem se math-objekti dijele na skupove i ne-skupove, dobro je različito ih označavati.
| Citat: | a onda se uvjerih da smo relacije označavali malim slovom 'ro' pa vidim i ovdje u ZF(štogod ta kratica krila,prema sadržaju bih rekao-Znanstvena Fantastika  ) ) |
Fantastika, ali ne baš znanstvena. 
Zermelo-Fraenkelova standardna teorija skupova.
http://www.cs.bilkent.edu.tr/~akman/jour-papers/air/node5.html
| Citat: | | se skupovi označavaju malim slovom) sa x : |
Stvar je u tome da, u ZF, _svi_ math-objekti su skupovi. Pa onda nema smisla svjesno se odreći polovice slovâ...
Osim toga, većina math-teorijâ primarne objekte koje proučava označava malim slovima: analiza realne brojeve, linearna algebra vektore... teorija skupova primarno proučava ('đenje!: ) skupove.
| Citat: | | x:=A ,i sad,tu su nastali problemi jer ne shvaćam simboliku ' :⇔ ',pa sam ja to shvatio kao:formulu ZF teorije imamo ako i samo ako x nije iz skupa B, |
Jednostavno, tako definiram formulu koja mi "ovisi" o z . Slično kao što funkciju koja mi "ovisi" o x definiram s npr. f(x):=3x+1 .
Za brojeve i izraze to je = , jednakost. Za formule, to je logička ekvivalencija, ⇔ .
| Citat: | | hm,nebi li trebalo pisati ako z nije iz B |
Bi.  Mah, cijelo vrijeme u elementarnoj označavamo "tipični element skupa" s x , pa sam to prenio i ovdje. :-/ Mah, cijelo vrijeme u elementarnoj označavamo "tipični element skupa" s x , pa sam to prenio i ovdje. :-/
| Citat: | | tako da se element x ne miješa sa skupom x(mada si to vjerojatno izbjegao supstitucijom x:=A). |
Što se toga tiče je ok (iako nije u skladu s nečim što se zove zvučnim imenom Konvencija o varijablama, ali to je ionako uglavnom estetska stvar), ali nije ok jer formula nije dobro opisana. Umjesto fi(z) na lijevoj strani bi trebalo ići fi(x) .
(Zapravo, striktno logički, to _jest_ svejedno. Varijable se, između ostalog da bi ih se imalo beskonačno mnogo i izbjegla konačnost abecede, označavaju redom s v0,v1,v2,.... . Tako da, kad kažemo da formula ima jednu slobodnu varijablu, podrazumijeva se da je to v0 . Ono što piše u zagradama je tada samo psihološka pomoć - ili, u ovom slučaju, odmoć. [ ] ) ] )
|
|
| [Vrh] |
|
|





