|
Fiksirajmo neki [latex]\varphi_{0}\in\mathbf{R}[/latex], to je kut koji određuje granu (argumenta/logaritma).
[i]Argument komplesknog broja[/i] (naime ovo je zapravo gradivo MA4) je funkcija [latex]\mathrm{Arg}^{\varphi_{0}}\colon\mathbf{C}_{\varphi_{0}}\to
\langle\varphi_{0},\varphi_{0}+2\pi][/latex]
definirana formulom [latex]\mathrm{Arg}^{\varphi_{0}}(z)=\varphi[/latex] takav da vrijedi [latex]z=|z| e^{i\varphi}[/latex], [latex]\varphi\in\langle\varphi_{0},\varphi_{0}+2\pi][/latex], gdje je [latex]\mathbf{C}_{\varphi_{0}}[/latex] kompleksna ravnina bez polupravca [latex]\{r e^{i\varphi_{0}}:r\geq 0\}[/latex].
[i]Logaritam kompleksnog broja[/i] je funkcija [latex]\mathrm{Ln}^{\varphi_{0}}\colon\mathbf{C}_{\varphi_{0}}\to
\mathbf{C}[/latex] definirana formulom [latex]\mathrm{Ln}^{\varphi_{0}}(z):=\mathrm{ln}(|z|)+i \mathrm{Arg}^{\varphi_{0}}[/latex], gdje je [latex]\mathrm{ln}[/latex] obična (realna) funkcija [i]prirodni logaritam[/i].
Evo npr. [latex]z=-1-i[/latex].
[latex]\mathrm{Ln}^{-\frac{\pi}{2}}(z)=?[/latex]
Napišemo z u obliku [latex]z=\sqrt{2} e^{i \frac{5\pi}{4}}[/latex], pri čemu smo birali [latex]\frac{5\pi}{4} \in\langle-\frac{\pi}{2},\frac{3\pi}{2}][/latex] pa je [latex]\mathrm{Ln}^{-\frac{\pi}{2}}(z)=\mathrm{ln}(\sqrt{2})+i \frac{5\pi}{4}[/latex]
[latex]\mathrm{Ln}^{-\pi}(z)=?[/latex]
Napišemo z u obliku [latex]z=\sqrt{2} e^{i (-\frac{3\pi}{4})}[/latex], pri čemu smo birali [latex]-\frac{3\pi}{4} \in\langle-\pi,\pi][/latex] pa je [latex]\mathrm{Ln}^{-\pi}(z)=\mathrm{ln}(\sqrt{2})+i (-\frac{3\pi}{4})[/latex]
Za svaki [latex]\varphi_{0}[/latex] vrijedi
[latex]e^{\mathrm{Ln}^{\varphi_{0}}(z)}=z[/latex]
te [latex]\left(\mathrm{Ln}^{\varphi_{0}}\right)' (z)=\frac{1}{z}[/latex],
a više derivacije se onda znaju izračunati.
Glavna grana argumenta/logaritma je ona za [latex]\varphi_{0}=-\pi[/latex]. (Dakle, kutovi [latex]\varphi[/latex] se uzimaju iz [latex]\langle-\pi,\pi][/latex]).
Ako trebamo izračunati [latex]f(A)[/latex] za [latex]f(\lambda)=\mathrm{Ln}^{\varphi_{0}}(\lambda)[/latex] i neki operator A, onda to radimo kao i za svaku drugu funkciju. Jedino trebamo paziti da spektar od A bude sadržan u domeni od [latex]\mathrm{Ln}^{\varphi_{0}}[/latex],
tj. da nijedna točka spektra ne leži na polupravcu [latex]\{r e^{i\varphi_{0}}:r\geq 0\}[/latex].
Ako nije precizirano koju granu logaritma računamo (tj. nije preciziran [latex]\varphi_{0}[/latex]), možemo je sami odabrati. Ipak, prioritet ima glavna grana logaritma (za [latex]\varphi_{0}=-\pi[/latex]), tj. (ukoliko je moguće) najradije se uzima baš nju. (Nije sad to nekakvo Pravilo, nego naprosto običaj. Naime ona se npr. na pozitivnim realnim brojevima podudara s običnim realnim logaritmom.)
Nešto slično se pričalo na
http://degiorgi.math.hr/forum/viewtopic.php?t=2747
Evo napr. operator A je zadan, a treba naći neki operator B takav da je [latex]2^B=A[/latex].
[latex]2^\lambda[/latex] zapravo po definiciji znači [latex]e^{\mathrm{ln}(2)\cdot\lambda}[/latex] (kako se na MA4 definira eksponencijalna fukcija pomoću standarnde eksponencijalne funkcije [latex]e^z[/latex]).
Prema tome jedan takav operator B ćemo dobiti formulom [latex]B=\frac{1}{\mathrm{ln}(2)}\mathrm{Ln}^{\varphi_{0}}(A)[/latex] za svaki (po volji odabrani) [latex]\varphi_{0}[/latex] takav da spektar od A nema točaka na izbačenom polupravcu. Za razne [latex]\varphi_{0}[/latex] bismo dobili razne operatore B (neki bi bili jednaki, neki bi bili različiti), ali svi bi zadovoljavali [latex]2^B=A[/latex].
Zato možemo "najzgodnije" izabrati [latex]\varphi_{0}[/latex].
Neka je nadalje npr. [latex]\mu(\lambda)=(\lambda+1)(\lambda-1)[/latex] te [latex]f(A)=f(-1)P_{1}+f(1)P_{2}[/latex].
Sada ne možemo računati glavnu granu logaritma [latex]\mathrm{Ln}^{-\pi}(A)[/latex] jer -1 nije u domeni od [latex]\mathrm{Ln}^{-\pi}[/latex]. Zato se odlučimo recimo za [latex]\varphi_{0}=-\frac{\pi}{2}[/latex], tj. računamo [latex]f(A)[/latex] za [latex]f(\lambda)=\mathrm{Ln}^{-\frac{\pi}{2}}(\lambda)[/latex].
[latex]f(-1)=\mathrm{ln}(1)+i\pi=i\pi[/latex]
[latex]f(1)=\mathrm{ln}(1)+i\cdot 0=0[/latex]
pa je [latex]f(A)=i\pi P_{1}[/latex].
Huh... Nadam se da je sad jasnije... :wink:
Fiksirajmo neki 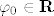 , to je kut koji određuje granu (argumenta/logaritma). , to je kut koji određuje granu (argumenta/logaritma).
Argument komplesknog broja (naime ovo je zapravo gradivo MA4) je funkcija 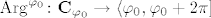
definirana formulom 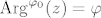 takav da vrijedi takav da vrijedi 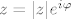 , , 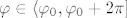 , gdje je , gdje je 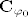 kompleksna ravnina bez polupravca kompleksna ravnina bez polupravca 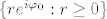 . .
Logaritam kompleksnog broja je funkcija 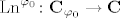 definirana formulom definirana formulom 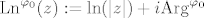 , gdje je , gdje je 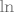 obična (realna) funkcija prirodni logaritam. obična (realna) funkcija prirodni logaritam.
Evo npr. 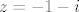 . .
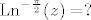
Napišemo z u obliku 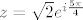 , pri čemu smo birali , pri čemu smo birali 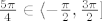 pa je pa je 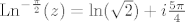
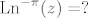
Napišemo z u obliku 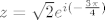 , pri čemu smo birali , pri čemu smo birali 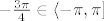 pa je pa je 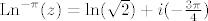
Za svaki 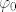 vrijedi vrijedi
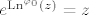
te 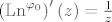 , ,
a više derivacije se onda znaju izračunati.
Glavna grana argumenta/logaritma je ona za  . (Dakle, kutovi . (Dakle, kutovi 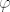 se uzimaju iz se uzimaju iz 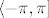 ). ).
Ako trebamo izračunati 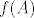 za za 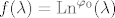 i neki operator A, onda to radimo kao i za svaku drugu funkciju. Jedino trebamo paziti da spektar od A bude sadržan u domeni od i neki operator A, onda to radimo kao i za svaku drugu funkciju. Jedino trebamo paziti da spektar od A bude sadržan u domeni od 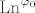 , ,
tj. da nijedna točka spektra ne leži na polupravcu 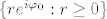 . .
Ako nije precizirano koju granu logaritma računamo (tj. nije preciziran 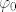 ), možemo je sami odabrati. Ipak, prioritet ima glavna grana logaritma (za ), možemo je sami odabrati. Ipak, prioritet ima glavna grana logaritma (za  ), tj. (ukoliko je moguće) najradije se uzima baš nju. (Nije sad to nekakvo Pravilo, nego naprosto običaj. Naime ona se npr. na pozitivnim realnim brojevima podudara s običnim realnim logaritmom.) ), tj. (ukoliko je moguće) najradije se uzima baš nju. (Nije sad to nekakvo Pravilo, nego naprosto običaj. Naime ona se npr. na pozitivnim realnim brojevima podudara s običnim realnim logaritmom.)
Nešto slično se pričalo na
http://degiorgi.math.hr/forum/viewtopic.php?t=2747
Evo napr. operator A je zadan, a treba naći neki operator B takav da je  . .
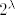 zapravo po definiciji znači zapravo po definiciji znači 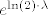 (kako se na MA4 definira eksponencijalna fukcija pomoću standarnde eksponencijalne funkcije (kako se na MA4 definira eksponencijalna fukcija pomoću standarnde eksponencijalne funkcije 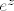 ). ).
Prema tome jedan takav operator B ćemo dobiti formulom 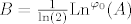 za svaki (po volji odabrani) za svaki (po volji odabrani) 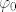 takav da spektar od A nema točaka na izbačenom polupravcu. Za razne takav da spektar od A nema točaka na izbačenom polupravcu. Za razne 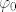 bismo dobili razne operatore B (neki bi bili jednaki, neki bi bili različiti), ali svi bi zadovoljavali bismo dobili razne operatore B (neki bi bili jednaki, neki bi bili različiti), ali svi bi zadovoljavali  . .
Zato možemo "najzgodnije" izabrati 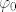 . .
Neka je nadalje npr. 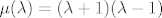 te te 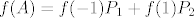 . .
Sada ne možemo računati glavnu granu logaritma 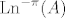 jer -1 nije u domeni od jer -1 nije u domeni od 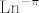 . Zato se odlučimo recimo za . Zato se odlučimo recimo za  , tj. računamo , tj. računamo 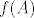 za za 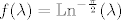 . .
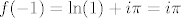
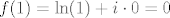
pa je 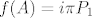 . .
Huh... Nadam se da je sad jasnije... 
|






