|
[quote="Markec"][color=blue][u]Zad.[/u]
Neka je P4={p: [b]R[/b]->[b]R[/b] polinom st<=3}, Q: P4->P4
Qp - polinom stupnja 2 ciji graf prolazi tockama
(-1, p(-1)), (0, p(0)), (1, p(1))
Dokazite da je Q lin. operator, odredite bazu za KerQ, ImQ ,
te odredite r(Q) i d(Q)[/color]
Uglavnom, imamo polinom
[latex] (Qp)(x)= p(0)+ \frac {p(1)-p(-1)}{2}x +(\frac {p(-1)+p(1)}{2} - p(0)) x^2
[/latex]
Q je linearni operator...
i sad
KerQ={p@P4: Qp=0}
i dalje su mi neke sitnice nejasne, pa ako bi netko mogao dovrsiti zadatak (bar odrediti bazu za KerQ)[/quote]
Rješavaš jednadžbu Qp=0polinom . p(x) se sigurno može zapisati kao ax^3+bx^2+cx+d . Vidi kako Qp izgleda u terminima koeficijenata a,b,c,d (njegove koeficijente preko vrijednosti od p u točkama 0,1,-1 si već odredio, samo sad uvrsti p(0)=d , p(1)=a+b+c+d , p(-1)=-a+b-c+d ), i izjednači ga s nulpolinomom -- odnosno, izjednači sve njegove koeficijente s nulom.
Dobit ćeš sustav s tri jednadžbe i 4 nepoznanice, te ćeš imati neko parametarski zadano rješenje. Zapiši kako p izgleda pod tim rješenjem (uvrsti a,b,c,d izražene npr. pomoću s i t ), izluči s i t iz čega možeš, i primijeti da si na taj način dobio proizvoljni element od KerQ kao linearnu kombinaciju dva polinoma (onaj uz s , i onaj uz t ). Dakle, ta dva polinoma čine skup izvodnica. Još provjeri da su nezavisni, i imaš bazu.
**
Drugi način (više misaon, manje računanja): pogledaj kako Q djeluje na bazi. Kanonska baza za P4 je {konstanta1,identiteta,kvadriranje,kubiranje} . Označimo te elemente redom s p1,p2,p3,p4 .
Iz teorema o interpolacijskom polinomu slijedi da Q ostavlja na miru sve polinome stupnja <=2 , specijalno p1,p2,p3 -- pa treba samo vidjeti što je Qp4(x) . Lako se vidi (možemo pogađati rješenje, znamo da je jedinstveno) da je to identiteta (mora prolaziti kroz (-1,-1),(0,0),(1,1) ), odnosno polinom p2 . To znači da je p4-p2 u jezgri. Također, iz onog što je rečeno na početku ovog odlomka slijedi da je slika od Q kompletan P3 (koji je naravno potprostor od P4 ), pa je r(Q)=3 . Po teoremu o rangu i defektu d(Q)=dimP4-r(Q)=4-3=1 , odnosno (p4-p2) je baza za jezgru od Q .
HTH,
| Markec (napisa): | Zad.
Neka je P4={p: R→R polinom st⇐3}, Q: P4→P4
Qp - polinom stupnja 2 ciji graf prolazi tockama
(-1, p(-1)), (0, p(0)), (1, p(1))
Dokazite da je Q lin. operator, odredite bazu za KerQ, ImQ ,
te odredite r(Q) i d(Q)
Uglavnom, imamo polinom
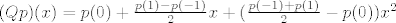
Q je linearni operator...
i sad
KerQ={p@P4: Qp=0}
i dalje su mi neke sitnice nejasne, pa ako bi netko mogao dovrsiti zadatak (bar odrediti bazu za KerQ) |
Rješavaš jednadžbu Qp=0polinom . p(x) se sigurno može zapisati kao ax^3+bx^2+cx+d . Vidi kako Qp izgleda u terminima koeficijenata a,b,c,d (njegove koeficijente preko vrijednosti od p u točkama 0,1,-1 si već odredio, samo sad uvrsti p(0)=d , p(1)=a+b+c+d , p(-1)=-a+b-c+d ), i izjednači ga s nulpolinomom – odnosno, izjednači sve njegove koeficijente s nulom.
Dobit ćeš sustav s tri jednadžbe i 4 nepoznanice, te ćeš imati neko parametarski zadano rješenje. Zapiši kako p izgleda pod tim rješenjem (uvrsti a,b,c,d izražene npr. pomoću s i t ), izluči s i t iz čega možeš, i primijeti da si na taj način dobio proizvoljni element od KerQ kao linearnu kombinaciju dva polinoma (onaj uz s , i onaj uz t ). Dakle, ta dva polinoma čine skup izvodnica. Još provjeri da su nezavisni, i imaš bazu.
**
Drugi način (više misaon, manje računanja): pogledaj kako Q djeluje na bazi. Kanonska baza za P4 je {konstanta1,identiteta,kvadriranje,kubiranje} . Označimo te elemente redom s p1,p2,p3,p4 .
Iz teorema o interpolacijskom polinomu slijedi da Q ostavlja na miru sve polinome stupnja ⇐2 , specijalno p1,p2,p3 – pa treba samo vidjeti što je Qp4(x) . Lako se vidi (možemo pogađati rješenje, znamo da je jedinstveno) da je to identiteta (mora prolaziti kroz (-1,-1),(0,0),(1,1) ), odnosno polinom p2 . To znači da je p4-p2 u jezgri. Također, iz onog što je rečeno na početku ovog odlomka slijedi da je slika od Q kompletan P3 (koji je naravno potprostor od P4 ), pa je r(Q)=3 . Po teoremu o rangu i defektu d(Q)=dimP4-r(Q)=4-3=1 , odnosno (p4-p2) je baza za jezgru od Q .
HTH,
|





