| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Vjeko
Forumaš(ica)

Pridružen/a: 26. 10. 2004. (17:33:06)
Postovi: (39)16
Spol: 
|
 Postano: 20:09 ned, 12. 12. 2004 Naslov: Kolokvijski fenomen Postano: 20:09 ned, 12. 12. 2004 Naslov: Kolokvijski fenomen |
    |
|
|
Ovom bih prilikom volio ukazati na jedan zanimljiv fenomen na koji sam naišao gledajući nedavno pristigle rezultate kolokvija iz EM1. Naime, vidljivo ja da lijep broj mojih kolega za koje znam da su dobri, štoviše odlični matematičari i dosadašnje kolokvije iz ostalih kolegija su dobro napisali, ne zna što je to indukcija., baš kao ni ja. Ostale zadatke napisali su dobro, a njima, kao i meni na bodovima sa zadatka iz indukcije stoji lijepa, okrugla nula. To što ja imam nulu, ne bi me toliko ni začudilo, ali za njih mi je neobično. Čak sam se i čuo s jednom kolegicom i ona mi je rekla da je zadatak predala i misli da joj je točan, ali dobila je nula bodova, a kao i u mom slučaju, predala ga je na zasebnom papiru. Da možda u tom grmu ne leži zec? Jer, pretpostavljam da bi čovjek već samo za bazu indukcije dobio bodić. Ali baš nula… A možda smo zbilja svi i napravili neku grešku u principu pa ako se zaista pojavila takva učestala greška, volio bih da ju netko istakne i naglasi.
Ovom bih prilikom volio ukazati na jedan zanimljiv fenomen na koji sam naišao gledajući nedavno pristigle rezultate kolokvija iz EM1. Naime, vidljivo ja da lijep broj mojih kolega za koje znam da su dobri, štoviše odlični matematičari i dosadašnje kolokvije iz ostalih kolegija su dobro napisali, ne zna što je to indukcija., baš kao ni ja. Ostale zadatke napisali su dobro, a njima, kao i meni na bodovima sa zadatka iz indukcije stoji lijepa, okrugla nula. To što ja imam nulu, ne bi me toliko ni začudilo, ali za njih mi je neobično. Čak sam se i čuo s jednom kolegicom i ona mi je rekla da je zadatak predala i misli da joj je točan, ali dobila je nula bodova, a kao i u mom slučaju, predala ga je na zasebnom papiru. Da možda u tom grmu ne leži zec? Jer, pretpostavljam da bi čovjek već samo za bazu indukcije dobio bodić. Ali baš nula… A možda smo zbilja svi i napravili neku grešku u principu pa ako se zaista pojavila takva učestala greška, volio bih da ju netko istakne i naglasi.
_________________  Mir i dug život! 
 Živi dugo i uspješno!  |
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Smith
Forumaš(ica)


Pridružen/a: 30. 10. 2004. (23:30:23)
Postovi: (178)16
Spol: 
Lokacija: {Tamo Gore}^{TM}
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 21:09 ned, 12. 12. 2004 Naslov: Re: Kolokvijski fenomen Postano: 21:09 ned, 12. 12. 2004 Naslov: Re: Kolokvijski fenomen |
    |
|
|
Ok, idemo redom.
Da, i mene je fenomen začudio. Činjenica je da je math-dokazivanje jedna prilično osjetljiva stvar, i sva poanta i snaga dokaza je u logičkom odmaku završne konkluzije od početnih premisâ. Kod indukcije je to naročito izraženo: iz tvrdnje da nešto vrijedi za samo jedan prirodni broj, i jedne univerzalne implikacije, ja mogu zaključiti univerzalnu tvrdnju da nešto vrijedi za svaki prirodan broj. Moćno, zar ne?
Samo treba tu univerzalnu implikaciju dokazati kako treba, _i iz ispravnih premisa_. Ona ima oblik (Ak@|N)(P(k)=>P(k+1)) . Nažalost, ovo je jedno od mjestâ gdje kvantifikatori _nisu_ distributivni prema logičkim veznicima, te gornji zapis _nije_ ekvivalentan zapisu (Ak@|N)P(k)=>(Ak@|N)P(k+1) . A to je, nažalost, ono što je jaako puno studenata, i to dobrih studenata, napravilo. U pretpostavci indukcije, napisali su "Pretpostavimo da P vrijedi za svaki k@|N ". :-(
E sad, zašto je to tako strašno? Kao što rekoh gore, sva bit math-dokaza je u, da tako kažem, "udaljenosti" između premisa i konkluzije. Ako sam dokazao nešto što je prilično daleko i na puno većoj "visini" od premisâ, dokaz je moćan.
Nažalost, vrijedi i dualno: ako sam dokazao neku od svojih pretpostavki, dokaz je bezvrijedan. Mislim da ćemo se složiti da iz P dokazati P (bar neformalno: ) stvarno nije neko umijeće. :roll:
A to je upravo ono što ispada kad čovjek čita gore skiciran "dokaz" indukcijom. Prvo se dokaže baza, a onda se iz pretpostavke _koja je potpuno jednaka onom što treba dokazati_ dokaže to isto (zapravo slabije: dokaže se da tvrdnja vrijedi za svaki prirodni broj od 2 nadalje. Tek s bazom to postaje ekvivalentno pretpostavci). Dokaz na taj način ima oblik dokaza P=>P , i zaista se tu ne dokazuje zapravo ništa.
E sad, činjenica je da su ti ljudi uglavnom bar bazu riješili kako treba, i obično je praksa da se za bazu dade koji bod. No kao što napisah gore, baza _tek_ pretvara taj napisan dokaz u dokaz oblika P=>P . Dakle, čak i uz nju dokaz zapravo nema logičke vrijednosti. Nema svrhe dokazati P(1) , ako već u sljedećem koraku pretpostavim puuno snažniju stvar (Ak@|N)P(k) .
Možda postoji i argument za suprotnu tezu ovdje, a to je princip "nema negativnih bodova". Odnosno, ako je netko napisao samo bazu, dobio je (ja mislim 1 ) bod. Može se argumentirati da ako je netko napisao _više_ od toga, kakvu god glupost napisao, nije fer kazniti ga oduzimanjem tog boda koji je već zaradio. To sad ovisi o asistentu Pažaninu, koji je ispravljao taj zadatak, i bit će na žalbama u utorak. Ja sam pričao s njim o tom problemu, i rekao mi je da je ionako davao samo jedan bod za sâmu bazu, te da smatra da ljudi valjda neće za jedan bod ići na žalbe. Možda vas je potcijenio... u svakom slučaju, osim baze koja može biti diskutabilna (iako sam prezentirao gore argument da ni ona ništa ne vrijedi u ovom kontekstu), smatram da nemate pravo na bodove.
Samo još jednu stvar da napomenem, za ljude koji ovo gledaju "izvana". Brucoši još nemaju dovoljno fluentno math-izražavanje (treba samo vidjeti što sve ja moram čitati na 1. zadatku :roll: ), i često im se tu debelo gleda kroz prste. No ovo je specifičan slučaj. Na vježbama je posvećeno nekoliko minuta nabrajanju (i možda pokazivanju primjerâ) najčešćih grešaka kod dokazivanja math-indukcijom, i ova je zasigurno bila spomenuta kao najozbiljnija. Dakle, bili ste upozoreni. Matematičkoj strogosti se morate naučiti prije ili kasnije. Ako vam netko eksplicitno kaže da je neko argumentiranje pogrešno, očekuje se da ga *ne* koristite. :-/
Ok, idemo redom.
Da, i mene je fenomen začudio. Činjenica je da je math-dokazivanje jedna prilično osjetljiva stvar, i sva poanta i snaga dokaza je u logičkom odmaku završne konkluzije od početnih premisâ. Kod indukcije je to naročito izraženo: iz tvrdnje da nešto vrijedi za samo jedan prirodni broj, i jedne univerzalne implikacije, ja mogu zaključiti univerzalnu tvrdnju da nešto vrijedi za svaki prirodan broj. Moćno, zar ne?
Samo treba tu univerzalnu implikaciju dokazati kako treba, _i iz ispravnih premisa_. Ona ima oblik (Ak@|N)(P(k)=>P(k+1)) . Nažalost, ovo je jedno od mjestâ gdje kvantifikatori _nisu_ distributivni prema logičkim veznicima, te gornji zapis _nije_ ekvivalentan zapisu (Ak@|N)P(k)=>(Ak@|N)P(k+1) . A to je, nažalost, ono što je jaako puno studenata, i to dobrih studenata, napravilo. U pretpostavci indukcije, napisali su "Pretpostavimo da P vrijedi za svaki k@|N ". 
E sad, zašto je to tako strašno? Kao što rekoh gore, sva bit math-dokaza je u, da tako kažem, "udaljenosti" između premisa i konkluzije. Ako sam dokazao nešto što je prilično daleko i na puno većoj "visini" od premisâ, dokaz je moćan.
Nažalost, vrijedi i dualno: ako sam dokazao neku od svojih pretpostavki, dokaz je bezvrijedan. Mislim da ćemo se složiti da iz P dokazati P (bar neformalno: ) stvarno nije neko umijeće. 
A to je upravo ono što ispada kad čovjek čita gore skiciran "dokaz" indukcijom. Prvo se dokaže baza, a onda se iz pretpostavke _koja je potpuno jednaka onom što treba dokazati_ dokaže to isto (zapravo slabije: dokaže se da tvrdnja vrijedi za svaki prirodni broj od 2 nadalje. Tek s bazom to postaje ekvivalentno pretpostavci). Dokaz na taj način ima oblik dokaza P=>P , i zaista se tu ne dokazuje zapravo ništa.
E sad, činjenica je da su ti ljudi uglavnom bar bazu riješili kako treba, i obično je praksa da se za bazu dade koji bod. No kao što napisah gore, baza _tek_ pretvara taj napisan dokaz u dokaz oblika P=>P . Dakle, čak i uz nju dokaz zapravo nema logičke vrijednosti. Nema svrhe dokazati P(1) , ako već u sljedećem koraku pretpostavim puuno snažniju stvar (Ak@|N)P(k) .
Možda postoji i argument za suprotnu tezu ovdje, a to je princip "nema negativnih bodova". Odnosno, ako je netko napisao samo bazu, dobio je (ja mislim 1 ) bod. Može se argumentirati da ako je netko napisao _više_ od toga, kakvu god glupost napisao, nije fer kazniti ga oduzimanjem tog boda koji je već zaradio. To sad ovisi o asistentu Pažaninu, koji je ispravljao taj zadatak, i bit će na žalbama u utorak. Ja sam pričao s njim o tom problemu, i rekao mi je da je ionako davao samo jedan bod za sâmu bazu, te da smatra da ljudi valjda neće za jedan bod ići na žalbe. Možda vas je potcijenio... u svakom slučaju, osim baze koja može biti diskutabilna (iako sam prezentirao gore argument da ni ona ništa ne vrijedi u ovom kontekstu), smatram da nemate pravo na bodove.
Samo još jednu stvar da napomenem, za ljude koji ovo gledaju "izvana". Brucoši još nemaju dovoljno fluentno math-izražavanje (treba samo vidjeti što sve ja moram čitati na 1. zadatku  ), i često im se tu debelo gleda kroz prste. No ovo je specifičan slučaj. Na vježbama je posvećeno nekoliko minuta nabrajanju (i možda pokazivanju primjerâ) najčešćih grešaka kod dokazivanja math-indukcijom, i ova je zasigurno bila spomenuta kao najozbiljnija. Dakle, bili ste upozoreni. Matematičkoj strogosti se morate naučiti prije ili kasnije. Ako vam netko eksplicitno kaže da je neko argumentiranje pogrešno, očekuje se da ga *ne* koristite. :-/ ), i često im se tu debelo gleda kroz prste. No ovo je specifičan slučaj. Na vježbama je posvećeno nekoliko minuta nabrajanju (i možda pokazivanju primjerâ) najčešćih grešaka kod dokazivanja math-indukcijom, i ova je zasigurno bila spomenuta kao najozbiljnija. Dakle, bili ste upozoreni. Matematičkoj strogosti se morate naučiti prije ili kasnije. Ako vam netko eksplicitno kaže da je neko argumentiranje pogrešno, očekuje se da ga *ne* koristite. :-/
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
Vjeko
Forumaš(ica)

Pridružen/a: 26. 10. 2004. (17:33:06)
Postovi: (39)16
Spol: 
|
 Postano: 18:37 pon, 13. 12. 2004 Naslov: Postano: 18:37 pon, 13. 12. 2004 Naslov: |
    |
|
|
[quote="veky"]smatram da nemate pravo na bodove.
[/quote]
Naravno, sad kad je ukazano na postojanje greške, ni ne pada mi na pamet tražiti nešto što mi ne pripada. Ja jedino objašnjenje i jesam tražio, i sad kad sam ga dobio na njemu sam zahvalan. Pa ipak, mislim da još dugujem neke odgovore na neke tvrdnje.
Najprije
[quote="Smith"]Kolega Vjeko, ne kuzim...
Pa radili smo indukciju kod asistenta Persea, zar ne? :?
[/quote]
Radili smo radili, i znam kako se indukcija računa, ali račun i nije sporan, sporno je objašnjenje.
[quote="veky"]Na vježbama je posvećeno nekoliko minuta nabrajanju (i možda pokazivanju primjerâ) najčešćih grešaka kod dokazivanja math-indukcijom, i ova je zasigurno bila spomenuta kao najozbiljnija. Dakle, bili ste upozoreni. Matematičkoj strogosti se morate naučiti prije ili kasnije. Ako vam netko eksplicitno kaže da je neko argumentiranje pogrešno, očekuje se da ga *ne* koristite. :-/
[/quote]
U ovoj se izjavi krije slična pogreška kao i naša. Riječ je o krivom kvantifikatoru, o korištenju «svi» umjesto «neki». :lol: Ovo je prosuđivanje o cjelini na osnovu poznavanja četvrtine. Ili, uzevši u obzir ovu izjavu,
[quote="Vincent Van Ear"]Kada se prisjetim dijela vježbi što se tiču indukcije,jedino čega se [u]izrazito[/u] sjećam je rečenica koju je asistent Pažanin repetivno konzumirao:
Pretpostavimo da vrijedi za [b]neki[/b] n@IN
Pretpostavimo da vrijedi za [b]neki[/b] n@IN
Pretpostavimo da vrijedi za [b]neki[/b] n@IN
.
.
.
U svakom zadatku je naglašavao riječ '[b]neki[/b]' .Lijepo. :D[/quote]
u najboljem slučaju, polovine. Razgovarao sam o tome s kolegama koji su napravili pogrešku iz grupe (paradoksalno, i oni, kao i ja, uglavnom spadaju u kategoriju onih koji su uvijek na nastavi), ali i ostalima, i oni se, kao ni ja ne sjećaju uopće tako nečega, nekih proučavanja te i takvih grešaka, niti postoji ikakav pismeni trag o tome i nikako nije bilo tako spektakularnih i epskih izjava kao «Keep off! You've been warned!». U stvari, ne morate vjerovati meni, kolega, koliko shvaćam, imate znance i u našoj grupi, pitajte njih. Naravno, ništa od toga ne oslobađa nas odgovornosti, ne mora nam nitko pokazati sve greške koje postoje da bismo znali da ih ne radimo. Osim toga, vjerojatno se pretpostavljalo da su neke stvari već same po sebi jasne.
Zapravo, čini se da je na ovom zadatku bilo zdravije samo izvesti račun i suzdržati se od suvišnih komentara, jer nam je tako netko u najgorem slučaju mogao reći da nam nešto nedostaje i odbiti koji bod, nego se previše trsiti i svojim, još uistinu neizbrušenim matematičkim rječnikom pokušati nešto objasniti i komentirati, a time i riskirati ovakav lapsus zbog kojega nam netko zbog našeg nerazumijevanja može poništiti cijeli zadatak.
[quote="veky"]Ja sam pričao s njim o tom problemu, i rekao mi je da je ionako davao samo jedan bod za sâmu bazu, te da smatra da ljudi valjda neće za jedan bod ići na žalbe. Možda vas je potcijenio... [/quote]
Dobro, ovo je pripisivanje krive motivacije. Ni jedan ni deset bodova gore-dolje nije toliko bitno koliko razumijevanje suštine čitave stvari. I zato ću sutra zbilja ići vidjeti svoj test, bez uvrede ikom i ako nije problem, samo zato da vidim što sam točno napisao, jer teško je sjetiti se baš svake riječi desetak dana unatrag, osobito zato što sam taj zadatak pisao u cajtnotu pa zato i u brzini, a nisam ni osobito obraćao pažnju na popratne komentare. Bodovi su, barem meni, na tom zadatku prestali biti važni čim je ustanovljeno postojanje greške.
No dobro, bar ću iz cijele priče izaći nešto pametniji.
| veky (napisa): | smatram da nemate pravo na bodove.
|
Naravno, sad kad je ukazano na postojanje greške, ni ne pada mi na pamet tražiti nešto što mi ne pripada. Ja jedino objašnjenje i jesam tražio, i sad kad sam ga dobio na njemu sam zahvalan. Pa ipak, mislim da još dugujem neke odgovore na neke tvrdnje.
Najprije
| Smith (napisa): | Kolega Vjeko, ne kuzim...
Pa radili smo indukciju kod asistenta Persea, zar ne? 
|
Radili smo radili, i znam kako se indukcija računa, ali račun i nije sporan, sporno je objašnjenje.
| veky (napisa): | Na vježbama je posvećeno nekoliko minuta nabrajanju (i možda pokazivanju primjerâ) najčešćih grešaka kod dokazivanja math-indukcijom, i ova je zasigurno bila spomenuta kao najozbiljnija. Dakle, bili ste upozoreni. Matematičkoj strogosti se morate naučiti prije ili kasnije. Ako vam netko eksplicitno kaže da je neko argumentiranje pogrešno, očekuje se da ga *ne* koristite. :-/
|
U ovoj se izjavi krije slična pogreška kao i naša. Riječ je o krivom kvantifikatoru, o korištenju «svi» umjesto «neki».  Ovo je prosuđivanje o cjelini na osnovu poznavanja četvrtine. Ili, uzevši u obzir ovu izjavu, Ovo je prosuđivanje o cjelini na osnovu poznavanja četvrtine. Ili, uzevši u obzir ovu izjavu,
| Vincent Van Ear (napisa): | Kada se prisjetim dijela vježbi što se tiču indukcije,jedino čega se izrazito sjećam je rečenica koju je asistent Pažanin repetivno konzumirao:
Pretpostavimo da vrijedi za neki n@IN
Pretpostavimo da vrijedi za neki n@IN
Pretpostavimo da vrijedi za neki n@IN
.
.
.
U svakom zadatku je naglašavao riječ 'neki' .Lijepo.  |
u najboljem slučaju, polovine. Razgovarao sam o tome s kolegama koji su napravili pogrešku iz grupe (paradoksalno, i oni, kao i ja, uglavnom spadaju u kategoriju onih koji su uvijek na nastavi), ali i ostalima, i oni se, kao ni ja ne sjećaju uopće tako nečega, nekih proučavanja te i takvih grešaka, niti postoji ikakav pismeni trag o tome i nikako nije bilo tako spektakularnih i epskih izjava kao «Keep off! You've been warned!». U stvari, ne morate vjerovati meni, kolega, koliko shvaćam, imate znance i u našoj grupi, pitajte njih. Naravno, ništa od toga ne oslobađa nas odgovornosti, ne mora nam nitko pokazati sve greške koje postoje da bismo znali da ih ne radimo. Osim toga, vjerojatno se pretpostavljalo da su neke stvari već same po sebi jasne.
Zapravo, čini se da je na ovom zadatku bilo zdravije samo izvesti račun i suzdržati se od suvišnih komentara, jer nam je tako netko u najgorem slučaju mogao reći da nam nešto nedostaje i odbiti koji bod, nego se previše trsiti i svojim, još uistinu neizbrušenim matematičkim rječnikom pokušati nešto objasniti i komentirati, a time i riskirati ovakav lapsus zbog kojega nam netko zbog našeg nerazumijevanja može poništiti cijeli zadatak.
| veky (napisa): | | Ja sam pričao s njim o tom problemu, i rekao mi je da je ionako davao samo jedan bod za sâmu bazu, te da smatra da ljudi valjda neće za jedan bod ići na žalbe. Možda vas je potcijenio... |
Dobro, ovo je pripisivanje krive motivacije. Ni jedan ni deset bodova gore-dolje nije toliko bitno koliko razumijevanje suštine čitave stvari. I zato ću sutra zbilja ići vidjeti svoj test, bez uvrede ikom i ako nije problem, samo zato da vidim što sam točno napisao, jer teško je sjetiti se baš svake riječi desetak dana unatrag, osobito zato što sam taj zadatak pisao u cajtnotu pa zato i u brzini, a nisam ni osobito obraćao pažnju na popratne komentare. Bodovi su, barem meni, na tom zadatku prestali biti važni čim je ustanovljeno postojanje greške.
No dobro, bar ću iz cijele priče izaći nešto pametniji.
_________________  Mir i dug život! 
 Živi dugo i uspješno!  |
|
| [Vrh] |
|
Kova
Forumaš(ica)


Pridružen/a: 27. 02. 2004. (23:13:50)
Postovi: (4B)16
Spol: 
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
 Postano: 19:56 pon, 13. 12. 2004 Naslov: Re: Kolokvijski fenomen Postano: 19:56 pon, 13. 12. 2004 Naslov: Re: Kolokvijski fenomen |
    |
|
|
[quote="veky"]Samo treba tu univerzalnu implikaciju dokazati kako treba, _i iz ispravnih premisa_. Ona ima oblik (Ak@|N)(P(k)=>P(k+1)) . Nažalost, ovo je jedno od mjestâ gdje kvantifikatori _nisu_ distributivni prema logičkim veznicima, te gornji zapis _nije_ ekvivalentan zapisu (Ak@|N)P(k)=>(Ak@|N)P(k+1) . A to je, nažalost, ono što je jaako puno studenata, i to dobrih studenata, napravilo. U pretpostavci indukcije, napisali su "Pretpostavimo da P vrijedi za svaki k@|N ". :-([/quote]
ok, call me blind/stupid/votevr
no koliko mene moj mozak sluzi, ovo je forma indukcije koju su meni uviejk tupili...... ovo u zagradama se kao podrazumijeva, a sad mi se cini da se cijelo vrijeme podrazumijevalo nesto sasvim krivo.....
(*)
baza n=1 (recimo)
pretp: n=n (da li ovo zapravo znaci da pretp. da nesto vrijedi za neki, pa onda dokazavsi da vrijedi i za n+1 to povlaci da vrijedi za sve?!!?)
korak... n=n+1 (dokazujemo za n+1)
blabla
jerbo..... prva verzija koju napisah je bila n=n (pretp da vrijedi za svaki n)
a obzirom na raspravu...... a i na razum kojeg upravo ukljucih.... nesto mi tu smrdi.....
dakle, u konacnici pitanje: ovo moje sto napisah(*) je ok?
i drugo, zasto se prije nije RIJECIMA govorilo? i ZAPISALO na plocu RIJECIMA?
a ne samo napisati n=n ili k=n ili neku inkarnaciju istog..... i smatrati da se podrazumijeva ovo 'neki n', kao sto rekoh, moj prvi impuls je bio reci 'za svaki'
a ja sam em slusala ipak prije dvije godine.... pa me ovo malo brine..... koliko zapravo ljudi i dalje misli da je 'za svaki'??
| veky (napisa): | Samo treba tu univerzalnu implikaciju dokazati kako treba, _i iz ispravnih premisa_. Ona ima oblik (Ak@|N)(P(k)⇒P(k+1)) . Nažalost, ovo je jedno od mjestâ gdje kvantifikatori _nisu_ distributivni prema logičkim veznicima, te gornji zapis _nije_ ekvivalentan zapisu (Ak@|N)P(k)⇒(Ak@|N)P(k+1) . A to je, nažalost, ono što je jaako puno studenata, i to dobrih studenata, napravilo. U pretpostavci indukcije, napisali su "Pretpostavimo da P vrijedi za svaki k@|N ".  |
ok, call me blind/stupid/votevr
no koliko mene moj mozak sluzi, ovo je forma indukcije koju su meni uviejk tupili...... ovo u zagradama se kao podrazumijeva, a sad mi se cini da se cijelo vrijeme podrazumijevalo nesto sasvim krivo.....
(*)
baza n=1 (recimo)
pretp: n=n (da li ovo zapravo znaci da pretp. da nesto vrijedi za neki, pa onda dokazavsi da vrijedi i za n+1 to povlaci da vrijedi za sve?!!?)
korak... n=n+1 (dokazujemo za n+1)
blabla
jerbo..... prva verzija koju napisah je bila n=n (pretp da vrijedi za svaki n)
a obzirom na raspravu...... a i na razum kojeg upravo ukljucih.... nesto mi tu smrdi.....
dakle, u konacnici pitanje: ovo moje sto napisah(*) je ok?
i drugo, zasto se prije nije RIJECIMA govorilo? i ZAPISALO na plocu RIJECIMA?
a ne samo napisati n=n ili k=n ili neku inkarnaciju istog..... i smatrati da se podrazumijeva ovo 'neki n', kao sto rekoh, moj prvi impuls je bio reci 'za svaki'
a ja sam em slusala ipak prije dvije godine.... pa me ovo malo brine..... koliko zapravo ljudi i dalje misli da je 'za svaki'??
_________________
It's not who you love. It's how.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 20:17 pon, 13. 12. 2004 Naslov: Postano: 20:17 pon, 13. 12. 2004 Naslov: |
    |
|
|
[quote="Vjeko"][quote="veky"]Na vježbama je posvećeno nekoliko minuta nabrajanju (i možda pokazivanju primjerâ) najčešćih grešaka kod dokazivanja math-indukcijom, i ova je zasigurno bila spomenuta kao najozbiljnija. Dakle, bili ste upozoreni. Matematičkoj strogosti se morate naučiti prije ili kasnije. Ako vam netko eksplicitno kaže da je neko argumentiranje pogrešno, očekuje se da ga *ne* koristite. :-/
[/quote]
U ovoj se izjavi krije slična pogreška kao i naša. Riječ je o krivom kvantifikatoru, o korištenju «svi» umjesto «neki». :lol:[/quote]
Sorry, ali vaša pogreška je u tome što ne čitate. :-P
Lijepo gore piše "Ako vam _netko_ eksplicitno kaže..." ;->
No dobro, dosta cjepidlačenja, idemo na bitnije stvari...
[quote] Ovo je prosuđivanje o cjelini na osnovu poznavanja četvrtine. Ili, uzevši u obzir ovu izjavu,
...
u najboljem slučaju, polovine.[/quote]
Ne znam što je za vas najbolji slučaj. :-/ Ja bih rekao, u najgorem slučaju 3/4 (jer definitivno vjerujem da je Mea ispričala to na vježbama), a u najboljem (iz naše perspektive), 1 cijelo. Za Ozrena zaista ne mogu garantirati, i lako mogu zamisliti da je, s obzirom na to da obično voli malo sporije objašnjavati, shvatio da kasni i malo brže prešao preko tog objašnjenja, no i dalje volim misliti da je to _rekao_. Naravno, ja nisam bio tamo... vi ste bili (nadam se). No prošle godine sam naučio da je sasvim moguće da "više od polovice" (jel tako HijenA? :-P ) studenata koji su bili na tom satu na vježbama, misli da nešto nisam rekao, dok ovi ostali znaju da jesam, i imaju to zapisano u bilježnici, tako da nažalost (i stvarno mi je žao zbog toga) nemam više baš puno povjerenja u izjave poput
[quote] Razgovarao sam o tome s kolegama koji su napravili pogrešku iz grupe (paradoksalno, i oni, kao i ja, uglavnom spadaju u kategoriju onih koji su uvijek na nastavi), ali i ostalima, i oni se, kao ni ja ne sjećaju uopće tako nečega, nekih proučavanja te i takvih grešaka, niti postoji ikakav pismeni trag o tome i nikako nije bilo tako spektakularnih i epskih izjava kao «Keep off! You've been warned!».[/quote]
No dobro, "spektakularno i epski" vjerujem da nije Ozrenov stil uopće, tako da me tu ne morate puno uvjeravati. :-) No i dalje mislim da je to rečeno.
[quote]Naravno, ništa od toga ne oslobađa nas odgovornosti, ne mora nam nitko pokazati sve greške koje postoje da bismo znali da ih ne radimo. Osim toga, vjerojatno se pretpostavljalo da su neke stvari već same po sebi jasne.[/quote]
Hm da. Naprimjer, da ako dokažete P pri tome koristeći P , stvarno niste ništa vrijedno napravili. :roll: S ovim bih se definitivno složio, da nije ovog čudnog Nesinog komentara dolje. :-( Možda stvarno to ima puno veće razmjere nego što smo mislili... :-/
[quote]Zapravo, čini se da je na ovom zadatku bilo zdravije samo izvesti račun i suzdržati se od suvišnih komentara, jer nam je tako netko u najgorem slučaju mogao reći da nam nešto nedostaje i odbiti koji bod, nego se previše trsiti i svojim, još uistinu neizbrušenim matematičkim rječnikom pokušati nešto objasniti i komentirati, a time i riskirati ovakav lapsus zbog kojega nam netko zbog našeg nerazumijevanja može poništiti cijeli zadatak.[/quote]
Donekle. Kao što rekoh, jedini argument na vašoj strani je princip "nema negativnih bodova", koji nažalost nije nigdje službeno formuliran, ali AFAIK, po njemu se obično ispravljalo /inače bi mnogi studenti završili u minusu: /.
[quote]Dobro, ovo je pripisivanje krive motivacije. Ni jedan ni deset bodova gore-dolje nije toliko bitno koliko razumijevanje suštine čitave stvari. I zato ću sutra zbilja ići vidjeti svoj test, bez uvrede ikom i ako nije problem, samo zato da vidim što sam točno napisao,[/quote]
Naravno. I ja Vas pozivam da to učinite. Naravno da ja nisam čak ni uopće vidio što ste _Vi_ napisali na tom zadatku... samo zaključujem nepotpunom indukcijom. ;-|
[quote]No dobro, bar ću iz cijele priče izaći nešto pametniji.[/quote]
Vjerovali ili ne, to je sva naša motivacija. I za skidanje bodova, i za rušenje, pa čak i za rušenje na komisiji. [:-/]
| Vjeko (napisa): | | veky (napisa): | Na vježbama je posvećeno nekoliko minuta nabrajanju (i možda pokazivanju primjerâ) najčešćih grešaka kod dokazivanja math-indukcijom, i ova je zasigurno bila spomenuta kao najozbiljnija. Dakle, bili ste upozoreni. Matematičkoj strogosti se morate naučiti prije ili kasnije. Ako vam netko eksplicitno kaže da je neko argumentiranje pogrešno, očekuje se da ga *ne* koristite. :-/
|
U ovoj se izjavi krije slična pogreška kao i naša. Riječ je o krivom kvantifikatoru, o korištenju «svi» umjesto «neki».  |
Sorry, ali vaša pogreška je u tome što ne čitate. 
Lijepo gore piše "Ako vam _netko_ eksplicitno kaže..." ;→
No dobro, dosta cjepidlačenja, idemo na bitnije stvari...
| Citat: | Ovo je prosuđivanje o cjelini na osnovu poznavanja četvrtine. Ili, uzevši u obzir ovu izjavu,
...
u najboljem slučaju, polovine. |
Ne znam što je za vas najbolji slučaj. :-/ Ja bih rekao, u najgorem slučaju 3/4 (jer definitivno vjerujem da je Mea ispričala to na vježbama), a u najboljem (iz naše perspektive), 1 cijelo. Za Ozrena zaista ne mogu garantirati, i lako mogu zamisliti da je, s obzirom na to da obično voli malo sporije objašnjavati, shvatio da kasni i malo brže prešao preko tog objašnjenja, no i dalje volim misliti da je to _rekao_. Naravno, ja nisam bio tamo... vi ste bili (nadam se). No prošle godine sam naučio da je sasvim moguće da "više od polovice" (jel tako HijenA?  ) studenata koji su bili na tom satu na vježbama, misli da nešto nisam rekao, dok ovi ostali znaju da jesam, i imaju to zapisano u bilježnici, tako da nažalost (i stvarno mi je žao zbog toga) nemam više baš puno povjerenja u izjave poput ) studenata koji su bili na tom satu na vježbama, misli da nešto nisam rekao, dok ovi ostali znaju da jesam, i imaju to zapisano u bilježnici, tako da nažalost (i stvarno mi je žao zbog toga) nemam više baš puno povjerenja u izjave poput
| Citat: | | Razgovarao sam o tome s kolegama koji su napravili pogrešku iz grupe (paradoksalno, i oni, kao i ja, uglavnom spadaju u kategoriju onih koji su uvijek na nastavi), ali i ostalima, i oni se, kao ni ja ne sjećaju uopće tako nečega, nekih proučavanja te i takvih grešaka, niti postoji ikakav pismeni trag o tome i nikako nije bilo tako spektakularnih i epskih izjava kao «Keep off! You've been warned!». |
No dobro, "spektakularno i epski" vjerujem da nije Ozrenov stil uopće, tako da me tu ne morate puno uvjeravati.  No i dalje mislim da je to rečeno. No i dalje mislim da je to rečeno.
| Citat: | | Naravno, ništa od toga ne oslobađa nas odgovornosti, ne mora nam nitko pokazati sve greške koje postoje da bismo znali da ih ne radimo. Osim toga, vjerojatno se pretpostavljalo da su neke stvari već same po sebi jasne. |
Hm da. Naprimjer, da ako dokažete P pri tome koristeći P , stvarno niste ništa vrijedno napravili.  S ovim bih se definitivno složio, da nije ovog čudnog Nesinog komentara dolje. S ovim bih se definitivno složio, da nije ovog čudnog Nesinog komentara dolje.  Možda stvarno to ima puno veće razmjere nego što smo mislili... :-/ Možda stvarno to ima puno veće razmjere nego što smo mislili... :-/
| Citat: | | Zapravo, čini se da je na ovom zadatku bilo zdravije samo izvesti račun i suzdržati se od suvišnih komentara, jer nam je tako netko u najgorem slučaju mogao reći da nam nešto nedostaje i odbiti koji bod, nego se previše trsiti i svojim, još uistinu neizbrušenim matematičkim rječnikom pokušati nešto objasniti i komentirati, a time i riskirati ovakav lapsus zbog kojega nam netko zbog našeg nerazumijevanja može poništiti cijeli zadatak. |
Donekle. Kao što rekoh, jedini argument na vašoj strani je princip "nema negativnih bodova", koji nažalost nije nigdje službeno formuliran, ali AFAIK, po njemu se obično ispravljalo /inače bi mnogi studenti završili u minusu: /.
| Citat: | | Dobro, ovo je pripisivanje krive motivacije. Ni jedan ni deset bodova gore-dolje nije toliko bitno koliko razumijevanje suštine čitave stvari. I zato ću sutra zbilja ići vidjeti svoj test, bez uvrede ikom i ako nije problem, samo zato da vidim što sam točno napisao, |
Naravno. I ja Vas pozivam da to učinite. Naravno da ja nisam čak ni uopće vidio što ste _Vi_ napisali na tom zadatku... samo zaključujem nepotpunom indukcijom. ;-|
| Citat: | | No dobro, bar ću iz cijele priče izaći nešto pametniji. |
Vjerovali ili ne, to je sva naša motivacija. I za skidanje bodova, i za rušenje, pa čak i za rušenje na komisiji. [:-/]
|
|
| [Vrh] |
|
Gost
|
 Postano: 21:14 pon, 13. 12. 2004 Naslov: Re: Kolokvijski fenomen Postano: 21:14 pon, 13. 12. 2004 Naslov: Re: Kolokvijski fenomen |
    |
|
|
[quote="Nesi"][quote="veky"]Samo treba tu univerzalnu implikaciju dokazati kako treba, _i iz ispravnih premisa_. Ona ima oblik (Ak@|N)(P(k)=>P(k+1)) . Nažalost, ovo je jedno od mjestâ gdje kvantifikatori _nisu_ distributivni prema logičkim veznicima, te gornji zapis _nije_ ekvivalentan zapisu (Ak@|N)P(k)=>(Ak@|N)P(k+1) . A to je, nažalost, ono što je jaako puno studenata, i to dobrih studenata, napravilo. U pretpostavci indukcije, napisali su "Pretpostavimo da P vrijedi za svaki k@|N ". :-([/quote]
ok, call me blind/stupid/votevr
no koliko mene moj mozak sluzi, ovo je forma indukcije koju su meni uviejk tupili...... ovo u zagradama se kao podrazumijeva, a sad mi se cini da se cijelo vrijeme podrazumijevalo nesto sasvim krivo..... [/quote]
Ne znam na što misliš "u zagradama"... zagrade su gore služile samo za grupiranje. Kao što napisah u gornjem odgovoru, sasvim je moguće da nerazumijevanje ima puno šire razmjere. :-(
[quote](*)
baza n=1 (recimo)
pretp: n=n (da li ovo zapravo znaci da pretp. da nesto vrijedi za neki, pa onda dokazavsi da vrijedi i za n+1 to povlaci da vrijedi za sve?!!?)
korak... n=n+1 (dokazujemo za n+1)
blabla
jerbo..... prva verzija koju napisah je bila n=n (pretp da vrijedi za svaki n)
a obzirom na raspravu...... [b]a i na razum kojeg upravo ukljucih[/b].... nesto mi tu smrdi.....
dakle, u konacnici pitanje: ovo moje sto napisah(*) je ok?[/quote]
Ok, idemo još jednom. Pun zapis aksioma matematičke indukcije glasi
[code:1]P(1) & (Ak@|N)(P(k)=>P(k+1)) => (An@|N)P(n)[/code:1]
, gdje je P nešto dosta komplicirano za definirati, ali neformalno recimo "neko svojstvo prirodnih brojeva" ( P(ž) znači da prirodni broj ž ima to svojstvo).
Dakle, indukcija (kao i većina teorema u mathu) ima oblik implikacije. Da bi se ona mogla iskoristiti (konzultiramo tablicu istinitosti), treba dokazati njenu pretpostavku, dakle
[code:1]P(1) & (Ak@|N)(P(k)=>P(k+1))[/code:1]
, i onda možemo izvući kao zaključak njenu posljedicu,
[code:1](An@|N)P(n)[/code:1]
, što je u većini slučajeva upravo ono što nam treba.
Dakle, treba dokazati P(1) & (Ak@|N)(P(k)=>P(k+1)) ,
i to ima oblik konjunkcije. Opet konzultiramo tablicu istinitosti, i vidimo da treba dokazati oba njena dijela:
[code:1]P(1)[/code:1]
i
[code:1](Ak@|N)(P(k)=>P(k+1)[/code:1]
, da bismo mogli zaključiti da ona vrijedi.
Ovo prvo se obično lako dokaže, i zove se baza. Ovo drugo se obično malo teže dokaže, i zove se korak. Bacimo se na to.
Ta izjava ima oblik univerzalne kvantifikacije po k@|N . Sad nažalost ne možemo konzultirati tablicu istinitosti (to bi bila kao fol konjunkcija beskonačno mnogo implikacijâ tipa (P(1)=>P(2))&(P(2)=>P(3))&.... ), pa moramo primijeniti neku drugu taktiku.
Razmišljamo ovako: ja moram, in effect, dokazati P(52)=>P(53) . No to moram napraviti tako da se u tom dokazu broj 52 može zamijeniti bilo kojim prirodnim brojem (zovem ga k ) (a broj 53 njegovim sljedbenikom). Na prvi pogled, to je stvarno dobro napraviti metodom "sve muhe jednim udarcem", odnosno pretpostaviti P(k) univerzalno. Ali gledajmo korak dalje... ako smo stvarno pretpostavili P(k) univerzalno, _čemu_ dovvaga dokazivati P(53) (i to, ironično, koristeći od naše univerzalne pretpostavke samo totalno loše odabran komad P(52) :-] )? To je onda stvarno samo specijalni slučaj naše pretpostavke, i nije ga nikakav problem dokazati. Pitamo se _zašto_ je to tako? Ofcourse -- zato što smo, silly us, kompletno pretpostavili upravo ono što smo trebali dokazati.
Dakle, treba nam nešto drugo. [u]Intuitivno[/u], trebamo dokazati P(52)=>P(53) , ali zapravo ne pretpostavljajući P(52) . Zašto to ne moramo pretpostavljati? Zato što će slijediti iz implikacije P(51)=>P(52) koju smo hopefully dokazali, jednom kad imamo P(51) . On će također slijediti iz P(50) , po implikaciji P(50)=>P(51) koju smo također već dokazali, i tako dalje... odnosno, preciznije, i tako bliže jedinici. :-)
Dakle, na neformalnoj razini, imamo nešto poput beskonačne varijante onog što se obično zove BSOMP. Sjetimo se što je BSOMP... kad jednom shvatimo da se dokaz od točke na koju smo došli račva u dvije grane, koje su međusobno izomorfne ("jednakog oblika", prelaze jedna u drugu jednostavnom zamjenom nekih slovâ nekim drugim slovima, pri čemu zadatak ostaje isti pri toj zamjeni), možemo dokazati samo _jednu_ od njih (svejedno koju), i iz toga će asistent znati zaključiti da smo znali dokazati i drugu. :-) Da umjesto dvije grane imamo njih 20 , koje su također izomorfne, dovoljno bi bilo dokazati samo _jednu_ od njih (napisavši na početak nešto poput "BSOMP da vrijedi prvi slučaj od njih 20 "). Ta jedna bi onda poslužila kao template pomoću kojeg bi se mogle dokazati i ostalih 19 , samo trivijalnim zamjenama slova ili uvrštavanjima specijalnih slučajeva. Da ih umjesto 20 imamo beskonačno, po jednu za svaki prirodni n , dovoljno bi bilo dokazati da za _neku_ granu od njih, za _neki_ n@|N , dokaz prolazi.
I zato korak indukcije ima takav oblik. Pretpostavi se da za _neki_ n@|N (koji se onda obično označi s k , da se izbjegne konfuzija s čudnom notacijom n=n+1 : ) vrijedi P(k) , i iz toga se dokaže P(k+1) . Na taj način dokazana je implikacija P(k)=>P(k+1) , koja je zaista template za sve implikacije u gornjoj beskonačnoj konjunkciji: P(1)=>P(2) , P(2)=>P(3) , itd. Dakle, dokazano je (Ak@|N)(P(k)=>P(k+1)) , i to bez pretpostavke (Ak@|N)P(k) (koja je naravno samo drugo ime za (An@|N)P(n) , što trebamo dokazati). A to je upravo ono što smo tražili.
Primijetimo podvučenu riječ "intuitivno" gore. To pretpostavlja da univerzalna kvantifikacija ima oblik "beskonačne konjunkcije", što baš i nije logički definabilno u istom frameworku (tzv. logika prvog reda) unutar koje se obično radi gorespomenuta indukcija. Postoji i _strogo logičko_ objašnjenje za to, no bojim se da je pomalo izvan opsega ove diskusije. Zato bih samo napisao jedan jednostavniji slučaj, koji dobro pokazuje zbog čega tu univerzalna kvantifikacija prelazi u egzistencijalnu.
To će biti za slučaj da P(k+1) zamijenimo tvrdnjom koja ne ovisi o k . Dakle, recimo da je to neka tvrdnja Q . To jest bitno pojednostavljivanje, ali će, vjerujem, pokazati što se događa.
Dakle, imamo (Ak@|N)(P(k)=>Q) . Pogledajmo tablicu istinitosti, i vidjet ćemo da je formula P=>Q ekvivalentna formuli (!P)vQ (i inutitivno, math-implikacija da P povlači Q upravo znači da P ne vrijedi, ili pak Q vrijedi).
So, imamo (Ak@|N)(!P(k)vQ) . Dakle, za svaki prirodan broj k , imamo dvije mogućnosti: u prvoj, !P(k) , a u drugoj, Q . No druga ne ovisi o k , pa ako vrijedi Q (neovisno o k ), ne mora uopće vrijediti nijedan !P(k) . S druge strane, ako Q ne vrijedi, druga mogućnost otpada _za svaki k _, pa uvijek vrijedi !P(k) . Sve u svemu, univerzalno imamo dva slučaja: u prvom Q , a u drugom (Ak@|N)!P(k) . Odnosno, imamo tvrdnju ((Ak@|N)!P(k))vQ . Ako je hoćemo napisati u obliku implikacije (da izvučemo tu implikaciju van), pogledajmo gore, moramo je dovesti u oblik !P'vQ' , odnosno prvi disjunkt mora biti negacija.
To možemo, ako se sjetimo formule za negiranje kvantifikatora -- negacija egzistencijalnog je univerzalni. Odnosno, naš prvi disjunkt, (Ak@|N)!P(k) je zapravo !(Ek@|N)P(k) . So, naša tvrdnja ima oblik
(!(Ek@|N)P(k))vQ , pa je možemo zapisati kao implikaciju
(Ek@|N)P(k)=>Q .
Sjetimo se od čega smo krenuli, i vidimo da je
(Ak@|N)(P(k)=>Q)
ekvivalentno s
((Ek@|N)P(k))=>Q .
Dakle, da _za svaki k _ tvrdnja P(k) povlači Q , ekvivalentno je tome da tvrdnja "za [b]neki[/b] k vrijedi P(k) " povlači Q . Naravno, kao što rekoh gore, kad Q ovisi također o k , stvari su kompliciranije jer se scopeovi zapetljavaju, ali u osnovi se događa ista stvar -- u pretpostavci, univerzalna kvantifikacija prelazi u egzistencijalnu. "Pretpostavimo da vrijedi _za neki k _".
[quote]i drugo, zasto se prije nije RIJECIMA govorilo? i ZAPISALO na plocu RIJECIMA?[/quote]
Što misliš? :-/
Da bih napisao ovo gore, trebalo mi je vremena kao za jedne prosječne vježbe ( 2 sata). Ok, s pripremom bi možda bilo malo manje. Ali definitivno, takve stvari se pri ovom programu i tempu _ne stignu_ napraviti.
Sad jasno zašto želim logiku i teoriju skupova na prvoj (zapravo nultoj) godini? Ne da mučim studente... već da im omogućim da govore konzistentno, i da ih ne razumijemo mi , već i oni sami sebe.
Gore je boldano tvoje "a i na razum kojeg upravo ukljucih"... koliko si dosad dokaza indukcijom napravila? Neću reći da su svi bili potpuno bezvrijedni, ali definitivno bi imalo više smisla da ti je ovo gore netko prije rekao, zar ne?
[quote]a ne samo napisati n=n ili k=n ili neku inkarnaciju istog..... i smatrati da se podrazumijeva ovo 'neki n', kao sto rekoh, moj prvi impuls je bio reci 'za svaki'[/quote]
Da, i ovo "n=n" isto vidjeh, i apsoštrumfno mi nije jasno kako netko može takvo nešto napisati. Što je onda korak, "n=n+1"?? :roll: "Za n=n+1" vrijedi sve, jer to ne zadovoljava nijedan n@|N .
Ako se već želi labelirati etape dokaza bez puno razmišljanja, standardne labele su "n=1","n=k"&"n=k+1" .
[quote]a ja sam em slusala ipak prije dvije godine.... pa me ovo malo brine..... koliko zapravo ljudi i dalje misli da je 'za svaki'??[/quote]
I mene isto (brine). :-S
| Nesi (napisa): | | veky (napisa): | Samo treba tu univerzalnu implikaciju dokazati kako treba, _i iz ispravnih premisa_. Ona ima oblik (Ak@|N)(P(k)⇒P(k+1)) . Nažalost, ovo je jedno od mjestâ gdje kvantifikatori _nisu_ distributivni prema logičkim veznicima, te gornji zapis _nije_ ekvivalentan zapisu (Ak@|N)P(k)⇒(Ak@|N)P(k+1) . A to je, nažalost, ono što je jaako puno studenata, i to dobrih studenata, napravilo. U pretpostavci indukcije, napisali su "Pretpostavimo da P vrijedi za svaki k@|N ".  |
ok, call me blind/stupid/votevr
no koliko mene moj mozak sluzi, ovo je forma indukcije koju su meni uviejk tupili...... ovo u zagradama se kao podrazumijeva, a sad mi se cini da se cijelo vrijeme podrazumijevalo nesto sasvim krivo..... |
Ne znam na što misliš "u zagradama"... zagrade su gore služile samo za grupiranje. Kao što napisah u gornjem odgovoru, sasvim je moguće da nerazumijevanje ima puno šire razmjere. 
| Citat: | (*)
baza n=1 (recimo)
pretp: n=n (da li ovo zapravo znaci da pretp. da nesto vrijedi za neki, pa onda dokazavsi da vrijedi i za n+1 to povlaci da vrijedi za sve?!!?)
korak... n=n+1 (dokazujemo za n+1)
blabla
jerbo..... prva verzija koju napisah je bila n=n (pretp da vrijedi za svaki n)
a obzirom na raspravu...... a i na razum kojeg upravo ukljucih.... nesto mi tu smrdi.....
dakle, u konacnici pitanje: ovo moje sto napisah(*) je ok? |
Ok, idemo još jednom. Pun zapis aksioma matematičke indukcije glasi
| Kod: | | P(1) & (Ak@|N)(P(k)=>P(k+1)) => (An@|N)P(n) |
, gdje je P nešto dosta komplicirano za definirati, ali neformalno recimo "neko svojstvo prirodnih brojeva" ( P(ž) znači da prirodni broj ž ima to svojstvo).
Dakle, indukcija (kao i većina teorema u mathu) ima oblik implikacije. Da bi se ona mogla iskoristiti (konzultiramo tablicu istinitosti), treba dokazati njenu pretpostavku, dakle
| Kod: | | P(1) & (Ak@|N)(P(k)=>P(k+1)) |
, i onda možemo izvući kao zaključak njenu posljedicu,
, što je u većini slučajeva upravo ono što nam treba.
Dakle, treba dokazati P(1) & (Ak@|N)(P(k)⇒P(k+1)) ,
i to ima oblik konjunkcije. Opet konzultiramo tablicu istinitosti, i vidimo da treba dokazati oba njena dijela:
i
| Kod: | | (Ak@|N)(P(k)=>P(k+1) |
, da bismo mogli zaključiti da ona vrijedi.
Ovo prvo se obično lako dokaže, i zove se baza. Ovo drugo se obično malo teže dokaže, i zove se korak. Bacimo se na to.
Ta izjava ima oblik univerzalne kvantifikacije po k@|N . Sad nažalost ne možemo konzultirati tablicu istinitosti (to bi bila kao fol konjunkcija beskonačno mnogo implikacijâ tipa (P(1)⇒P(2))&(P(2)⇒P(3))&.... ), pa moramo primijeniti neku drugu taktiku.
Razmišljamo ovako: ja moram, in effect, dokazati P(52)⇒P(53) . No to moram napraviti tako da se u tom dokazu broj 52 može zamijeniti bilo kojim prirodnim brojem (zovem ga k ) (a broj 53 njegovim sljedbenikom). Na prvi pogled, to je stvarno dobro napraviti metodom "sve muhe jednim udarcem", odnosno pretpostaviti P(k) univerzalno. Ali gledajmo korak dalje... ako smo stvarno pretpostavili P(k) univerzalno, _čemu_ dovvaga dokazivati P(53) (i to, ironično, koristeći od naše univerzalne pretpostavke samo totalno loše odabran komad P(52) :-] )? To je onda stvarno samo specijalni slučaj naše pretpostavke, i nije ga nikakav problem dokazati. Pitamo se _zašto_ je to tako? Ofcourse – zato što smo, silly us, kompletno pretpostavili upravo ono što smo trebali dokazati.
Dakle, treba nam nešto drugo. Intuitivno, trebamo dokazati P(52)⇒P(53) , ali zapravo ne pretpostavljajući P(52) . Zašto to ne moramo pretpostavljati? Zato što će slijediti iz implikacije P(51)⇒P(52) koju smo hopefully dokazali, jednom kad imamo P(51) . On će također slijediti iz P(50) , po implikaciji P(50)⇒P(51) koju smo također već dokazali, i tako dalje... odnosno, preciznije, i tako bliže jedinici. 
Dakle, na neformalnoj razini, imamo nešto poput beskonačne varijante onog što se obično zove BSOMP. Sjetimo se što je BSOMP... kad jednom shvatimo da se dokaz od točke na koju smo došli račva u dvije grane, koje su međusobno izomorfne ("jednakog oblika", prelaze jedna u drugu jednostavnom zamjenom nekih slovâ nekim drugim slovima, pri čemu zadatak ostaje isti pri toj zamjeni), možemo dokazati samo _jednu_ od njih (svejedno koju), i iz toga će asistent znati zaključiti da smo znali dokazati i drugu.  Da umjesto dvije grane imamo njih 20 , koje su također izomorfne, dovoljno bi bilo dokazati samo _jednu_ od njih (napisavši na početak nešto poput "BSOMP da vrijedi prvi slučaj od njih 20 "). Ta jedna bi onda poslužila kao template pomoću kojeg bi se mogle dokazati i ostalih 19 , samo trivijalnim zamjenama slova ili uvrštavanjima specijalnih slučajeva. Da ih umjesto 20 imamo beskonačno, po jednu za svaki prirodni n , dovoljno bi bilo dokazati da za _neku_ granu od njih, za _neki_ n@|N , dokaz prolazi. Da umjesto dvije grane imamo njih 20 , koje su također izomorfne, dovoljno bi bilo dokazati samo _jednu_ od njih (napisavši na početak nešto poput "BSOMP da vrijedi prvi slučaj od njih 20 "). Ta jedna bi onda poslužila kao template pomoću kojeg bi se mogle dokazati i ostalih 19 , samo trivijalnim zamjenama slova ili uvrštavanjima specijalnih slučajeva. Da ih umjesto 20 imamo beskonačno, po jednu za svaki prirodni n , dovoljno bi bilo dokazati da za _neku_ granu od njih, za _neki_ n@|N , dokaz prolazi.
I zato korak indukcije ima takav oblik. Pretpostavi se da za _neki_ n@|N (koji se onda obično označi s k , da se izbjegne konfuzija s čudnom notacijom n=n+1 : ) vrijedi P(k) , i iz toga se dokaže P(k+1) . Na taj način dokazana je implikacija P(k)⇒P(k+1) , koja je zaista template za sve implikacije u gornjoj beskonačnoj konjunkciji: P(1)⇒P(2) , P(2)⇒P(3) , itd. Dakle, dokazano je (Ak@|N)(P(k)⇒P(k+1)) , i to bez pretpostavke (Ak@|N)P(k) (koja je naravno samo drugo ime za (An@|N)P(n) , što trebamo dokazati). A to je upravo ono što smo tražili.
Primijetimo podvučenu riječ "intuitivno" gore. To pretpostavlja da univerzalna kvantifikacija ima oblik "beskonačne konjunkcije", što baš i nije logički definabilno u istom frameworku (tzv. logika prvog reda) unutar koje se obično radi gorespomenuta indukcija. Postoji i _strogo logičko_ objašnjenje za to, no bojim se da je pomalo izvan opsega ove diskusije. Zato bih samo napisao jedan jednostavniji slučaj, koji dobro pokazuje zbog čega tu univerzalna kvantifikacija prelazi u egzistencijalnu.
To će biti za slučaj da P(k+1) zamijenimo tvrdnjom koja ne ovisi o k . Dakle, recimo da je to neka tvrdnja Q . To jest bitno pojednostavljivanje, ali će, vjerujem, pokazati što se događa.
Dakle, imamo (Ak@|N)(P(k)⇒Q) . Pogledajmo tablicu istinitosti, i vidjet ćemo da je formula P⇒Q ekvivalentna formuli (!P)vQ (i inutitivno, math-implikacija da P povlači Q upravo znači da P ne vrijedi, ili pak Q vrijedi).
So, imamo (Ak@|N)(!P(k)vQ) . Dakle, za svaki prirodan broj k , imamo dvije mogućnosti: u prvoj, !P(k) , a u drugoj, Q . No druga ne ovisi o k , pa ako vrijedi Q (neovisno o k ), ne mora uopće vrijediti nijedan !P(k) . S druge strane, ako Q ne vrijedi, druga mogućnost otpada _za svaki k _, pa uvijek vrijedi !P(k) . Sve u svemu, univerzalno imamo dva slučaja: u prvom Q , a u drugom (Ak@|N)!P(k) . Odnosno, imamo tvrdnju ((Ak@|N)!P(k))vQ . Ako je hoćemo napisati u obliku implikacije (da izvučemo tu implikaciju van), pogledajmo gore, moramo je dovesti u oblik !P'vQ' , odnosno prvi disjunkt mora biti negacija.
To možemo, ako se sjetimo formule za negiranje kvantifikatora – negacija egzistencijalnog je univerzalni. Odnosno, naš prvi disjunkt, (Ak@|N)!P(k) je zapravo !(Ek@|N)P(k) . So, naša tvrdnja ima oblik
(!(Ek@|N)P(k))vQ , pa je možemo zapisati kao implikaciju
(Ek@|N)P(k)⇒Q .
Sjetimo se od čega smo krenuli, i vidimo da je
(Ak@|N)(P(k)⇒Q)
ekvivalentno s
((Ek@|N)P(k))⇒Q .
Dakle, da _za svaki k _ tvrdnja P(k) povlači Q , ekvivalentno je tome da tvrdnja "za neki k vrijedi P(k) " povlači Q . Naravno, kao što rekoh gore, kad Q ovisi također o k , stvari su kompliciranije jer se scopeovi zapetljavaju, ali u osnovi se događa ista stvar – u pretpostavci, univerzalna kvantifikacija prelazi u egzistencijalnu. "Pretpostavimo da vrijedi _za neki k _".
| Citat: | | i drugo, zasto se prije nije RIJECIMA govorilo? i ZAPISALO na plocu RIJECIMA? |
Što misliš? :-/
Da bih napisao ovo gore, trebalo mi je vremena kao za jedne prosječne vježbe ( 2 sata). Ok, s pripremom bi možda bilo malo manje. Ali definitivno, takve stvari se pri ovom programu i tempu _ne stignu_ napraviti.
Sad jasno zašto želim logiku i teoriju skupova na prvoj (zapravo nultoj) godini? Ne da mučim studente... već da im omogućim da govore konzistentno, i da ih ne razumijemo mi , već i oni sami sebe.
Gore je boldano tvoje "a i na razum kojeg upravo ukljucih"... koliko si dosad dokaza indukcijom napravila? Neću reći da su svi bili potpuno bezvrijedni, ali definitivno bi imalo više smisla da ti je ovo gore netko prije rekao, zar ne?
| Citat: | | a ne samo napisati n=n ili k=n ili neku inkarnaciju istog..... i smatrati da se podrazumijeva ovo 'neki n', kao sto rekoh, moj prvi impuls je bio reci 'za svaki' |
Da, i ovo "n=n" isto vidjeh, i apsoštrumfno mi nije jasno kako netko može takvo nešto napisati. Što je onda korak, "n=n+1"??  "Za n=n+1" vrijedi sve, jer to ne zadovoljava nijedan n@|N . "Za n=n+1" vrijedi sve, jer to ne zadovoljava nijedan n@|N .
Ako se već želi labelirati etape dokaza bez puno razmišljanja, standardne labele su "n=1","n=k"&"n=k+1" .
| Citat: | | a ja sam em slusala ipak prije dvije godine.... pa me ovo malo brine..... koliko zapravo ljudi i dalje misli da je 'za svaki'?? |
I mene isto (brine). :-S
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
Vjeko
Forumaš(ica)

Pridružen/a: 26. 10. 2004. (17:33:06)
Postovi: (39)16
Spol: 
|
 Postano: 8:08 uto, 14. 12. 2004 Naslov: Postano: 8:08 uto, 14. 12. 2004 Naslov: |
    |
|
|
[quote="veky"]
Za Ozrena zaista ne mogu garantirati, i lako mogu zamisliti da je, s obzirom na to da obično voli malo sporije objašnjavati, shvatio da kasni i malo brže prešao preko tog objašnjenja, no i dalje volim misliti da je to _rekao_. Naravno, ja nisam bio tamo... vi ste bili (nadam se). No prošle godine sam naučio da je sasvim moguće da "više od polovice" (jel tako HijenA? :-P ) studenata koji su bili na tom satu na vježbama, misli da nešto nisam rekao, dok ovi ostali znaju da jesam, i imaju to zapisano u bilježnici, tako da nažalost (i stvarno mi je žao zbog toga) nemam više baš puno povjerenja u izjave poput ...
[/quote]
Rekao sam, imate kod koga kod nas provjeriti. Ali da se razumijemo, ništa ja ne zamjeram asistentu Peršeu, on je nama dobro pokazao kako treba, što je i jedino što se od asistenta mora očekivati. Jedino što je ona "We told you so"-tvrdnja diskutabilna.
| veky (napisa): |
Za Ozrena zaista ne mogu garantirati, i lako mogu zamisliti da je, s obzirom na to da obično voli malo sporije objašnjavati, shvatio da kasni i malo brže prešao preko tog objašnjenja, no i dalje volim misliti da je to _rekao_. Naravno, ja nisam bio tamo... vi ste bili (nadam se). No prošle godine sam naučio da je sasvim moguće da "više od polovice" (jel tako HijenA?  ) studenata koji su bili na tom satu na vježbama, misli da nešto nisam rekao, dok ovi ostali znaju da jesam, i imaju to zapisano u bilježnici, tako da nažalost (i stvarno mi je žao zbog toga) nemam više baš puno povjerenja u izjave poput ... ) studenata koji su bili na tom satu na vježbama, misli da nešto nisam rekao, dok ovi ostali znaju da jesam, i imaju to zapisano u bilježnici, tako da nažalost (i stvarno mi je žao zbog toga) nemam više baš puno povjerenja u izjave poput ...
|
Rekao sam, imate kod koga kod nas provjeriti. Ali da se razumijemo, ništa ja ne zamjeram asistentu Peršeu, on je nama dobro pokazao kako treba, što je i jedino što se od asistenta mora očekivati. Jedino što je ona "We told you so"-tvrdnja diskutabilna.
_________________  Mir i dug život! 
 Živi dugo i uspješno!  |
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 16:22 uto, 14. 12. 2004 Naslov: Postano: 16:22 uto, 14. 12. 2004 Naslov: |
    |
|
|
[quote="veky"]
Ne znam što je za vas najbolji slučaj. :-/ Ja bih rekao, u najgorem slučaju 3/4 (jer definitivno vjerujem da je Mea ispričala to na vježbama), a u najboljem (iz naše perspektive), 1 cijelo. Za Ozrena zaista ne mogu garantirati, i lako mogu zamisliti da je, s obzirom na to da obično voli malo sporije objašnjavati, shvatio da kasni i malo brže prešao preko tog objašnjenja, no i dalje volim misliti da je to _rekao_. Naravno, ja nisam bio tamo... vi ste bili (nadam se). No prošle godine sam naučio da je sasvim moguće da "više od polovice" (jel tako HijenA? :-P ) studenata koji su bili na tom satu na vježbama, misli da nešto nisam rekao, dok ovi ostali znaju da jesam, i imaju to zapisano u bilježnici, tako da nažalost (i stvarno mi je žao zbog toga) nemam više baš puno povjerenja u izjave poput
[quote] Razgovarao sam o tome s kolegama koji su napravili pogrešku iz grupe (paradoksalno, i oni, kao i ja, uglavnom spadaju u kategoriju onih koji su uvijek na nastavi), ali i ostalima, i oni se, kao ni ja ne sjećaju uopće tako nečega, nekih proučavanja te i takvih grešaka, niti postoji ikakav pismeni trag o tome i nikako nije bilo tako spektakularnih i epskih izjava kao «Keep off! You've been warned!».[/quote][/quote]
tako je...ali to svejedno ne znaci da ja nisam bio u pravu. eto, pred hansom sam pitao jednog kolegu (koji je bio sa mnom na vjezbama) kako su mu se svidjele tvoje vjezbe, a on je rekao, doslovce, katastrofa i da nije nista shvatio. ja te opet pitam: zar stvarno mislis da kad, od 70 studenata, dolazi na vjezbe njih 10 sve u redu sa samim predavanjima, te da je problem u studentima? na to mi pitanje nisi nikad odgovorio.
mislim, ovo je zadnje sto cu reci o toj temi. dosta je puta vec prozvakana, ne zelim biti :OT:, i ne zelim se vise na to vracati. bilo pa proslo.
| veky (napisa): |
Ne znam što je za vas najbolji slučaj. :-/ Ja bih rekao, u najgorem slučaju 3/4 (jer definitivno vjerujem da je Mea ispričala to na vježbama), a u najboljem (iz naše perspektive), 1 cijelo. Za Ozrena zaista ne mogu garantirati, i lako mogu zamisliti da je, s obzirom na to da obično voli malo sporije objašnjavati, shvatio da kasni i malo brže prešao preko tog objašnjenja, no i dalje volim misliti da je to _rekao_. Naravno, ja nisam bio tamo... vi ste bili (nadam se). No prošle godine sam naučio da je sasvim moguće da "više od polovice" (jel tako HijenA?  ) studenata koji su bili na tom satu na vježbama, misli da nešto nisam rekao, dok ovi ostali znaju da jesam, i imaju to zapisano u bilježnici, tako da nažalost (i stvarno mi je žao zbog toga) nemam više baš puno povjerenja u izjave poput ) studenata koji su bili na tom satu na vježbama, misli da nešto nisam rekao, dok ovi ostali znaju da jesam, i imaju to zapisano u bilježnici, tako da nažalost (i stvarno mi je žao zbog toga) nemam više baš puno povjerenja u izjave poput
| Citat: | | Razgovarao sam o tome s kolegama koji su napravili pogrešku iz grupe (paradoksalno, i oni, kao i ja, uglavnom spadaju u kategoriju onih koji su uvijek na nastavi), ali i ostalima, i oni se, kao ni ja ne sjećaju uopće tako nečega, nekih proučavanja te i takvih grešaka, niti postoji ikakav pismeni trag o tome i nikako nije bilo tako spektakularnih i epskih izjava kao «Keep off! You've been warned!». |
|
tako je...ali to svejedno ne znaci da ja nisam bio u pravu. eto, pred hansom sam pitao jednog kolegu (koji je bio sa mnom na vjezbama) kako su mu se svidjele tvoje vjezbe, a on je rekao, doslovce, katastrofa i da nije nista shvatio. ja te opet pitam: zar stvarno mislis da kad, od 70 studenata, dolazi na vjezbe njih 10 sve u redu sa samim predavanjima, te da je problem u studentima? na to mi pitanje nisi nikad odgovorio.
mislim, ovo je zadnje sto cu reci o toj temi. dosta je puta vec prozvakana, ne zelim biti  , i ne zelim se vise na to vracati. bilo pa proslo. , i ne zelim se vise na to vracati. bilo pa proslo.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 17:33 uto, 14. 12. 2004 Naslov: Postano: 17:33 uto, 14. 12. 2004 Naslov: |
    |
|
|
[quote="HijenA"]
tako je...ali to svejedno ne znaci da ja nisam bio u pravu.[/quote]
Sad ne pričamo o tome. Posljednji put kad smo pričali o tome, povukao si se bez ispunjenog obećanja. Znaš dobro o čemu pričam.
[quote] eto, pred hansom sam pitao jednog kolegu (koji je bio sa mnom na vjezbama) kako su mu se svidjele tvoje vjezbe, a on je rekao, doslovce, katastrofa i da nije nista shvatio. ja te opet pitam: zar stvarno mislis da kad, od 70 studenata, dolazi na vjezbe njih 10 sve u redu sa samim predavanjima, te da je problem u studentima? na to mi pitanje nisi nikad odgovorio.[/quote]
Jesam, samo taj dio moje priče nikad nisi želio slušati. A ti meni nisi odgovorio na deset pitanja iz mog zadnjeg pm-a.
[quote]mislim, ovo je zadnje sto cu reci o toj temi. dosta je puta vec prozvakana, ne zelim biti :OT:, i ne zelim se vise na to vracati. bilo pa proslo.[/quote]
Odgovorio bih ti na pm, kad ne bih znao da na pmove ne odgovaraš. :-/
| HijenA (napisa): |
tako je...ali to svejedno ne znaci da ja nisam bio u pravu. |
Sad ne pričamo o tome. Posljednji put kad smo pričali o tome, povukao si se bez ispunjenog obećanja. Znaš dobro o čemu pričam.
| Citat: | | eto, pred hansom sam pitao jednog kolegu (koji je bio sa mnom na vjezbama) kako su mu se svidjele tvoje vjezbe, a on je rekao, doslovce, katastrofa i da nije nista shvatio. ja te opet pitam: zar stvarno mislis da kad, od 70 studenata, dolazi na vjezbe njih 10 sve u redu sa samim predavanjima, te da je problem u studentima? na to mi pitanje nisi nikad odgovorio. |
Jesam, samo taj dio moje priče nikad nisi želio slušati. A ti meni nisi odgovorio na deset pitanja iz mog zadnjeg pm-a.
| Citat: | mislim, ovo je zadnje sto cu reci o toj temi. dosta je puta vec prozvakana, ne zelim biti  , i ne zelim se vise na to vracati. bilo pa proslo. , i ne zelim se vise na to vracati. bilo pa proslo. |
Odgovorio bih ti na pm, kad ne bih znao da na pmove ne odgovaraš. :-/
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
 Postano: 18:55 čet, 16. 12. 2004 Naslov: Re: Kolokvijski fenomen Postano: 18:55 čet, 16. 12. 2004 Naslov: Re: Kolokvijski fenomen |
    |
|
|
[quote="Veky neulogirani"][quote]i drugo, zasto se prije nije RIJECIMA govorilo? i ZAPISALO na plocu RIJECIMA?[/quote]
Što misliš? :-/
Da bih napisao ovo gore, trebalo mi je vremena kao za jedne prosječne vježbe ( 2 sata). Ok, s pripremom bi možda bilo malo manje. Ali definitivno, takve stvari se pri ovom programu i tempu _ne stignu_ napraviti.[/quote]
zapravo sam mislila na sljedece:
ne pisati [latex]\forall k \in N[/latex] vec pisati [b]za neki [/b][latex]k \in N[/latex]
na ploci nisam (I believe) NIKADA vidjela da pise 'pretpostavimo da za neki k iz N vrijedi'
to su mozda rekli - ali to ispari...... :roll:
a jedino pisano bi bilo 'n=k' ili 'n=n' bez icega vise, uz, kao sto rekoh [u]mozda[/u] receno, ali cisto sumnjam.....
a cini se da je upravo tu big problem - prvih par puta bi bas rijecima trebalo zapisati 'pretp. da za NEKI k iz N vrijedi....' <ubaci tvrdnju> 'idemo provjeriti da li vrijedi za k+1'....<blabla dalje>
a tako necega se ne sjecam.....
[quote]Sad jasno zašto želim logiku i teoriju skupova na prvoj (zapravo nultoj) godini? Ne da mučim studente... već da im omogućim da govore konzistentno, i da ih ne razumijemo mi , već i oni sami sebe.[/quote]
:g:
[quote]Gore je boldano tvoje "a i na razum kojeg upravo ukljucih"... koliko si dosad dokaza indukcijom napravila? Neću reći da su svi bili potpuno bezvrijedni, ali definitivno bi imalo više smisla da ti je ovo gore netko prije rekao, zar ne?[/quote]
pobogu DA!!!
tuzno je da tek na trecoj godini postanem svjesna sto indukcija zbilja jest, a za nju mi pile vec 7 godina.... ali taj famozni 'neki' mi prije (u srednjoj) nije bas nesto posebno znacio
a na faxu su ga zaboravili propisno istaknuti.....
[quote][quote]a ne samo napisati n=n ili k=n ili neku inkarnaciju istog..... i smatrati da se podrazumijeva ovo 'neki n', kao sto rekoh, moj prvi impuls je bio reci 'za svaki'[/quote]
Da, i ovo "n=n" isto vidjeh, i apsoštrumfno mi nije jasno kako netko može takvo nešto napisati. Što je onda korak, "n=n+1"?? :roll: "Za n=n+1" vrijedi sve, jer to ne zadovoljava nijedan n@|N .
Ako se već želi labelirati etape dokaza bez puno razmišljanja, standardne labele su "n=1","n=k"&"n=k+1" .[/quote]
meni su to uglavnom bile samo labele.......
cinimise da mi je tek sad jasno zasto mi nikad nije sve stimalo s indukcijom...... uvijek mi je nes fallio i nikad mi nije 'legla'
do sada :g:
tnx Veky :klapklap:
ovak sad zgledas: :bis: :g:
[quote][quote]a ja sam em slusala ipak prije dvije godine.... pa me ovo malo brine..... koliko zapravo ljudi i dalje misli da je 'za svaki'??[/quote]
I mene isto (brine). :-S[/quote]
mozda ne bi bilo losa inicijativa napisati ne jedan papircek - jedan mali dokaz, JAKO istaknuti ovo 'za neki'.... posebno naglasiti da to nije 'za svaki' jer onda cemu uopce dokazivati...... i staviti link na ovu raspravu - i pokeljiti po faxu....
mislim da je to bitnija informacija studentima od raznoraznih plakata koji vise po zgradi..... :g:
| Veky neulogirani (napisa): | | Citat: | | i drugo, zasto se prije nije RIJECIMA govorilo? i ZAPISALO na plocu RIJECIMA? |
Što misliš? :-/
Da bih napisao ovo gore, trebalo mi je vremena kao za jedne prosječne vježbe ( 2 sata). Ok, s pripremom bi možda bilo malo manje. Ali definitivno, takve stvari se pri ovom programu i tempu _ne stignu_ napraviti. |
zapravo sam mislila na sljedece:
ne pisati 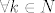 vec pisati za neki vec pisati za neki 
na ploci nisam (I believe) NIKADA vidjela da pise 'pretpostavimo da za neki k iz N vrijedi'
to su mozda rekli - ali to ispari...... 
a jedino pisano bi bilo 'n=k' ili 'n=n' bez icega vise, uz, kao sto rekoh mozda receno, ali cisto sumnjam.....
a cini se da je upravo tu big problem - prvih par puta bi bas rijecima trebalo zapisati 'pretp. da za NEKI k iz N vrijedi....' <ubaci tvrdnju> 'idemo provjeriti da li vrijedi za k+1'....<blabla dalje>
a tako necega se ne sjecam.....
| Citat: | | Sad jasno zašto želim logiku i teoriju skupova na prvoj (zapravo nultoj) godini? Ne da mučim studente... već da im omogućim da govore konzistentno, i da ih ne razumijemo mi , već i oni sami sebe. |

| Citat: | | Gore je boldano tvoje "a i na razum kojeg upravo ukljucih"... koliko si dosad dokaza indukcijom napravila? Neću reći da su svi bili potpuno bezvrijedni, ali definitivno bi imalo više smisla da ti je ovo gore netko prije rekao, zar ne? |
pobogu DA!!!
tuzno je da tek na trecoj godini postanem svjesna sto indukcija zbilja jest, a za nju mi pile vec 7 godina.... ali taj famozni 'neki' mi prije (u srednjoj) nije bas nesto posebno znacio
a na faxu su ga zaboravili propisno istaknuti.....
| Citat: | | Citat: | | a ne samo napisati n=n ili k=n ili neku inkarnaciju istog..... i smatrati da se podrazumijeva ovo 'neki n', kao sto rekoh, moj prvi impuls je bio reci 'za svaki' |
Da, i ovo "n=n" isto vidjeh, i apsoštrumfno mi nije jasno kako netko može takvo nešto napisati. Što je onda korak, "n=n+1"??  "Za n=n+1" vrijedi sve, jer to ne zadovoljava nijedan n@|N . "Za n=n+1" vrijedi sve, jer to ne zadovoljava nijedan n@|N .
Ako se već želi labelirati etape dokaza bez puno razmišljanja, standardne labele su "n=1","n=k"&"n=k+1" . |
meni su to uglavnom bile samo labele.......
cinimise da mi je tek sad jasno zasto mi nikad nije sve stimalo s indukcijom...... uvijek mi je nes fallio i nikad mi nije 'legla'
do sada 
tnx Veky 
ovak sad zgledas:  
| Citat: | | Citat: | | a ja sam em slusala ipak prije dvije godine.... pa me ovo malo brine..... koliko zapravo ljudi i dalje misli da je 'za svaki'?? |
I mene isto (brine). :-S |
mozda ne bi bilo losa inicijativa napisati ne jedan papircek - jedan mali dokaz, JAKO istaknuti ovo 'za neki'.... posebno naglasiti da to nije 'za svaki' jer onda cemu uopce dokazivati...... i staviti link na ovu raspravu - i pokeljiti po faxu....
mislim da je to bitnija informacija studentima od raznoraznih plakata koji vise po zgradi..... 
_________________
It's not who you love. It's how.
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 21:27 čet, 16. 12. 2004 Naslov: Re: Kolokvijski fenomen Postano: 21:27 čet, 16. 12. 2004 Naslov: Re: Kolokvijski fenomen |
    |
|
|
[quote="Nesi"][quote="Veky neulogirani"][quote]i drugo, zasto se prije nije RIJECIMA govorilo? i ZAPISALO na plocu RIJECIMA?[/quote]
Što misliš? :-/
Da bih napisao ovo gore, trebalo mi je vremena kao za jedne prosječne vježbe ( 2 sata). Ok, s pripremom bi možda bilo malo manje. Ali definitivno, takve stvari se pri ovom programu i tempu _ne stignu_ napraviti.[/quote]
zapravo sam mislila na sljedece:
ne pisati [latex]\forall k \in N[/latex] vec pisati [b]za neki [/b][latex]k \in N[/latex]
na ploci nisam (I believe) NIKADA vidjela da pise 'pretpostavimo da za neki k iz N vrijedi'[/quote]
Pa iskreno se nadam da nisi ni vidjela da piše [latex]\forall k\in\bf N[/latex] (u pretpostavci).
[quote]to su mozda rekli - ali to ispari...... :roll:[/quote]
Hm... pa da ti i piše u bilježnici iz kolegija koji si slušala prije dvije godine, jednako bi dosad isparilo kao i iz glave... ne li?
A eto, Vincentu očito nije isparilo što mu je as.Pažanin govorio... :-)
[quote]a jedino pisano bi bilo 'n=k' ili 'n=n' bez icega vise, uz, kao sto rekoh [u]mozda[/u] receno, ali cisto sumnjam..... [/quote]
Mi smo to rekli. Bar se nadam, svi. Jer u vježbama po kojima svi radimo (krckovim), bilo je eksplicitno naglašeno kao česta greška. A što se tiče pisanja, čitaj dolje...
[quote]a cini se da je upravo tu big problem - prvih par puta bi bas rijecima trebalo zapisati 'pretp. da za NEKI k iz N vrijedi....' <ubaci tvrdnju> 'idemo provjeriti da li vrijedi za k+1'....<blabla dalje>
a tako necega se ne sjecam..... [/quote]
The problem is, ljudima se previše na prvoj godini tupi s izomorfizmom intuitivnog shvaćanja i strogo logičkog kvantificiranja. I zato (IMO) ljudi imaju toliko problema sa shvaćanjem implikacije, zato mnogi ne kuže poantu dokaza metodom kontradikcije, prazan skup im predstavlja konceptualne probleme, i hrpa drugih stvari.
Kakve to veze ima s ovim? Kod mnogo njih, pogotovo ovih naprednijih studenata (koji su češće i napravili tu grešku), kvantifikatori su samo nešto što se onako "ofrlje" doda na izjavu, čisto kao neko pojašnjenje. I u tom mindsetu, [latex]\forall[/latex] znači "razmišljam univerzalno" (ono što engleski jezik označava članom "a"), dok [latex]\exists[/latex] znači "razmišljam partikularno" (ono što se u engleskom označava s "the"). A to u mnogim primjerima dovodi do gadnih miskoncepcijâ. Nemogućnost shvaćanja da za sve elemente praznog skupa vrijedi bilo što, je jedna od njih. Ovo o čemu ovdje pričamo je druga.
Jer stvarno, u tom mindsetu, čovjek samo želi reći "ovo što tu pišem, moći će se pretpostaviti, i iz toga dokazati što već treba, što god k bio. Razmišljam univerzalno". Da smo napisali na ploču "za [b]neki[/b]", i to podvukli/istakli/whatever, dogodilo bi se nešto još gore /iako bi se možda za to dobilo više bodova: /. Čovjek bi rekao "aha, razmišljam partikularno", dokazao da recimo P(1)=>P(2) , i gotova stvar. Suptilne stvari poput dosega pojedinih pretpostavki, i ostali detalji koji su bolno detaljno raspisani u gornjem postu, ostaju zauvijek skriveni.
Zato ja jednostavno eksplicitno upozorim ljude da ne smiju napisati "za svaki", i objasnim im zašto (otprilike kao ono što napisah gore, samo kraće: ), ali ne pišem ni "neki", jer bih to vjerojatno prije ili kasnije napisao kao "[latex]\exists[/latex]", a iz gore opisanih razlogâ, mislim da bi ih to zbunilo još više. Jednostavno objasnim šprancu, dam intuitivno objašnjenje zašto ona radi, i nakon toga koristim labele "n=1","n=k"&"n=k+1" , uz napomenu da će o striktnim scopeovima pojedinih varijabli ovdje naučiti tek nešto kasnije.
(Osim toga, kad se piše strogo simbolički, nesporazum nestaje. Samo treba zatvoriti zagradu na pravom mjestu.
"(.za svaki k.)[b]([/b]pretpostavimo da vrijedi P(k) ...i iz toga dokažimo P(k+1)...[b])[/b]" je sasvim ok. No ljudi onda pišu polusimbolički, jednostavno ne stave zagrade, i u prvom retku ostane samo
za svaki k, pretpostavimo da vrijedi P(k).
Još se to onda "prevede" na klasični Analiza-dijalekt, koji stavlja kvantifikatore na kraj, i dobiješ
pretpostavimo da vrijedi P(k) za svaki k ,
dakle, katastrofu.)
[quote]tuzno je da tek na trecoj godini postanem svjesna sto indukcija zbilja jest, a za nju mi pile vec 7 godina.... ali taj famozni 'neki' mi prije (u srednjoj) nije bas nesto posebno znacio
a na faxu su ga zaboravili propisno istaknuti..... [/quote]
Da ti pravo kažem, nemam blagog pojma gdje bi ljudi ovo (što gore napisah) trebali čuti. Pravo mjesto bi bila neka nulta godina, gdje se uči jezik i samo jezik. [size=9](Pa zaBoga, ne učiš npr. norveški tako da te netko baci u Norvešku i pusti te da učiš metodom pokušaja i pogrešaka... prvo imaš bar neku probnu simulaciju.)[/size] Ovako, stvarno to ostavljam "za poslije", kao i hrpu stvari, misleći "a valjda će to naučiti na logici/teoriji_skupova/...", no nekako više nisam siguran da je to dobra taktika. Anyhow, uvijek postoji hr.sci.matematika , gdje se mogu raspisati koliko želim. ;-)
[quote]meni su to uglavnom bile samo labele.......
cinimise da mi je tek sad jasno zasto mi nikad nije sve stimalo s indukcijom...... uvijek mi je nes fallio i nikad mi nije 'legla'
do sada :g:[/quote]
Meni se čini da je tako sa svim math-nerazumijevanjima. Glavni problem je što se uči obrnutim redom. Skoro svaku stvar prvo naučiš kao glupu mehaničku metodu, a tek onda, često i desetak godina kasnije, naučiš _zašto_, dovvaga. :-/
[quote]mozda ne bi bilo losa inicijativa napisati ne jedan papircek - jedan mali dokaz, JAKO istaknuti ovo 'za neki'.... posebno naglasiti da to nije 'za svaki' jer onda cemu uopce dokazivati...... i staviti link na ovu raspravu - i pokeljiti po faxu.... [/quote]
Imam kričavozeleni link na mom siteu. To je najviše što se usudim, da ne bi opet netko počeo kako ja imam "svoje uvrnuto viđenje stvari", kako mu namećem svoju filozofiju svijeta, i slično. Čak i na ovom Forumu, triput sam razmislio mogu li to ovdje napisati.
No ti, kao objektivni promatrač;-), možeš to uraditi. Na math nema licence... slobodno čini s mojim postovima što želiš.
[quote]mislim da je to bitnija informacija studentima od raznoraznih plakata koji vise po zgradi..... :g:[/quote]
Apsolutno se slažem. No pitanje je koliko bi se studenata složilo s time...
| Nesi (napisa): | | Veky neulogirani (napisa): | | Citat: | | i drugo, zasto se prije nije RIJECIMA govorilo? i ZAPISALO na plocu RIJECIMA? |
Što misliš? :-/
Da bih napisao ovo gore, trebalo mi je vremena kao za jedne prosječne vježbe ( 2 sata). Ok, s pripremom bi možda bilo malo manje. Ali definitivno, takve stvari se pri ovom programu i tempu _ne stignu_ napraviti. |
zapravo sam mislila na sljedece:
ne pisati 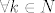 vec pisati za neki vec pisati za neki 
na ploci nisam (I believe) NIKADA vidjela da pise 'pretpostavimo da za neki k iz N vrijedi' |
Pa iskreno se nadam da nisi ni vidjela da piše 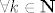 (u pretpostavci). (u pretpostavci).
| Citat: | to su mozda rekli - ali to ispari......  |
Hm... pa da ti i piše u bilježnici iz kolegija koji si slušala prije dvije godine, jednako bi dosad isparilo kao i iz glave... ne li?
A eto, Vincentu očito nije isparilo što mu je as.Pažanin govorio... 
| Citat: | | a jedino pisano bi bilo 'n=k' ili 'n=n' bez icega vise, uz, kao sto rekoh mozda receno, ali cisto sumnjam..... |
Mi smo to rekli. Bar se nadam, svi. Jer u vježbama po kojima svi radimo (krckovim), bilo je eksplicitno naglašeno kao česta greška. A što se tiče pisanja, čitaj dolje...
| Citat: | a cini se da je upravo tu big problem - prvih par puta bi bas rijecima trebalo zapisati 'pretp. da za NEKI k iz N vrijedi....' <ubaci tvrdnju> 'idemo provjeriti da li vrijedi za k+1'....<blabla dalje>
a tako necega se ne sjecam..... |
The problem is, ljudima se previše na prvoj godini tupi s izomorfizmom intuitivnog shvaćanja i strogo logičkog kvantificiranja. I zato (IMO) ljudi imaju toliko problema sa shvaćanjem implikacije, zato mnogi ne kuže poantu dokaza metodom kontradikcije, prazan skup im predstavlja konceptualne probleme, i hrpa drugih stvari.
Kakve to veze ima s ovim? Kod mnogo njih, pogotovo ovih naprednijih studenata (koji su češće i napravili tu grešku), kvantifikatori su samo nešto što se onako "ofrlje" doda na izjavu, čisto kao neko pojašnjenje. I u tom mindsetu, 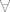 znači "razmišljam univerzalno" (ono što engleski jezik označava članom "a"), dok znači "razmišljam univerzalno" (ono što engleski jezik označava članom "a"), dok 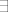 znači "razmišljam partikularno" (ono što se u engleskom označava s "the"). A to u mnogim primjerima dovodi do gadnih miskoncepcijâ. Nemogućnost shvaćanja da za sve elemente praznog skupa vrijedi bilo što, je jedna od njih. Ovo o čemu ovdje pričamo je druga. znači "razmišljam partikularno" (ono što se u engleskom označava s "the"). A to u mnogim primjerima dovodi do gadnih miskoncepcijâ. Nemogućnost shvaćanja da za sve elemente praznog skupa vrijedi bilo što, je jedna od njih. Ovo o čemu ovdje pričamo je druga.
Jer stvarno, u tom mindsetu, čovjek samo želi reći "ovo što tu pišem, moći će se pretpostaviti, i iz toga dokazati što već treba, što god k bio. Razmišljam univerzalno". Da smo napisali na ploču "za neki", i to podvukli/istakli/whatever, dogodilo bi se nešto još gore /iako bi se možda za to dobilo više bodova: /. Čovjek bi rekao "aha, razmišljam partikularno", dokazao da recimo P(1)⇒P(2) , i gotova stvar. Suptilne stvari poput dosega pojedinih pretpostavki, i ostali detalji koji su bolno detaljno raspisani u gornjem postu, ostaju zauvijek skriveni.
Zato ja jednostavno eksplicitno upozorim ljude da ne smiju napisati "za svaki", i objasnim im zašto (otprilike kao ono što napisah gore, samo kraće: ), ali ne pišem ni "neki", jer bih to vjerojatno prije ili kasnije napisao kao " ", a iz gore opisanih razlogâ, mislim da bi ih to zbunilo još više. Jednostavno objasnim šprancu, dam intuitivno objašnjenje zašto ona radi, i nakon toga koristim labele "n=1","n=k"&"n=k+1" , uz napomenu da će o striktnim scopeovima pojedinih varijabli ovdje naučiti tek nešto kasnije. ", a iz gore opisanih razlogâ, mislim da bi ih to zbunilo još više. Jednostavno objasnim šprancu, dam intuitivno objašnjenje zašto ona radi, i nakon toga koristim labele "n=1","n=k"&"n=k+1" , uz napomenu da će o striktnim scopeovima pojedinih varijabli ovdje naučiti tek nešto kasnije.
(Osim toga, kad se piše strogo simbolički, nesporazum nestaje. Samo treba zatvoriti zagradu na pravom mjestu.
"(.za svaki k.)(pretpostavimo da vrijedi P(k) ...i iz toga dokažimo P(k+1)...)" je sasvim ok. No ljudi onda pišu polusimbolički, jednostavno ne stave zagrade, i u prvom retku ostane samo
za svaki k, pretpostavimo da vrijedi P(k).
Još se to onda "prevede" na klasični Analiza-dijalekt, koji stavlja kvantifikatore na kraj, i dobiješ
pretpostavimo da vrijedi P(k) za svaki k ,
dakle, katastrofu.)
| Citat: | tuzno je da tek na trecoj godini postanem svjesna sto indukcija zbilja jest, a za nju mi pile vec 7 godina.... ali taj famozni 'neki' mi prije (u srednjoj) nije bas nesto posebno znacio
a na faxu su ga zaboravili propisno istaknuti..... |
Da ti pravo kažem, nemam blagog pojma gdje bi ljudi ovo (što gore napisah) trebali čuti. Pravo mjesto bi bila neka nulta godina, gdje se uči jezik i samo jezik. (Pa zaBoga, ne učiš npr. norveški tako da te netko baci u Norvešku i pusti te da učiš metodom pokušaja i pogrešaka... prvo imaš bar neku probnu simulaciju.) Ovako, stvarno to ostavljam "za poslije", kao i hrpu stvari, misleći "a valjda će to naučiti na logici/teoriji_skupova/...", no nekako više nisam siguran da je to dobra taktika. Anyhow, uvijek postoji hr.sci.matematika , gdje se mogu raspisati koliko želim. 
| Citat: | meni su to uglavnom bile samo labele.......
cinimise da mi je tek sad jasno zasto mi nikad nije sve stimalo s indukcijom...... uvijek mi je nes fallio i nikad mi nije 'legla'
do sada  |
Meni se čini da je tako sa svim math-nerazumijevanjima. Glavni problem je što se uči obrnutim redom. Skoro svaku stvar prvo naučiš kao glupu mehaničku metodu, a tek onda, često i desetak godina kasnije, naučiš _zašto_, dovvaga. :-/
| Citat: | | mozda ne bi bilo losa inicijativa napisati ne jedan papircek - jedan mali dokaz, JAKO istaknuti ovo 'za neki'.... posebno naglasiti da to nije 'za svaki' jer onda cemu uopce dokazivati...... i staviti link na ovu raspravu - i pokeljiti po faxu.... |
Imam kričavozeleni link na mom siteu. To je najviše što se usudim, da ne bi opet netko počeo kako ja imam "svoje uvrnuto viđenje stvari", kako mu namećem svoju filozofiju svijeta, i slično. Čak i na ovom Forumu, triput sam razmislio mogu li to ovdje napisati.
No ti, kao objektivni promatrač , možeš to uraditi. Na math nema licence... slobodno čini s mojim postovima što želiš. , možeš to uraditi. Na math nema licence... slobodno čini s mojim postovima što želiš.
| Citat: | mislim da je to bitnija informacija studentima od raznoraznih plakata koji vise po zgradi.....  |
Apsolutno se slažem. No pitanje je koliko bi se studenata složilo s time...
|
|
| [Vrh] |
|
Vjeko
Forumaš(ica)

Pridružen/a: 26. 10. 2004. (17:33:06)
Postovi: (39)16
Spol: 
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 1:22 pet, 17. 12. 2004 Naslov: Postano: 1:22 pet, 17. 12. 2004 Naslov: |
    |
|
|
[quote="Vjeko"][quote="veky"]
Imam kričavozeleni link na mom siteu.[/quote]
Da, baš sam vidio. Je li izbor boje po meni :mrgreen: ?[/quote]
Možda podsvjesno. ;-)
BTW što ti je to na čelu? :-k
[quote]Inicijativa nije loša i definitivno ne može nikome škoditi. Imam osjećaj da većina ljudi i ne shvaća da bi trebala pročitati ovu raspravu.[/quote]
Kao što rekoh, podržavam zamisao da Nesi (ili netko drugi) to napravi.
[quote]Također nisam siguran bih li prije trebao svima zahvaliti na sudjelovanju u raspravi ili se ispričati na pokretanju ovog topica, jer je diskusija u pojedinim trenucima bila prilično vruća i prevruća i kao da sam dirnuo u osinje gnijezdo. :oops:[/quote]
Mah, to je samo HijenA... :-)
Osim toga, što god bilo, ti tome nisi kriv. Zanimalo te zašto si izgubio bodove, odgovor si dobio (možda malo predetaljan za tvoj ukus, ali tako je to često na ovom Forumu: ). Što se dalje događa u diskusiji, možeš čitati ako te zanima, možeš odmahnuti rukom, možeš i sudjelovati ako želiš, ali u svakom slučaju, nisi odgovoran za ono što drugi pišu. Mi smo svi odrasli ljudi -- ili bar tako, s različitim uspjesima, glumimo. ;-)
| Vjeko (napisa): | | veky (napisa): |
Imam kričavozeleni link na mom siteu. |
Da, baš sam vidio. Je li izbor boje po meni  ? ? |
Možda podsvjesno. 
BTW što ti je to na čelu? 
| Citat: | | Inicijativa nije loša i definitivno ne može nikome škoditi. Imam osjećaj da većina ljudi i ne shvaća da bi trebala pročitati ovu raspravu. |
Kao što rekoh, podržavam zamisao da Nesi (ili netko drugi) to napravi.
| Citat: | Također nisam siguran bih li prije trebao svima zahvaliti na sudjelovanju u raspravi ili se ispričati na pokretanju ovog topica, jer je diskusija u pojedinim trenucima bila prilično vruća i prevruća i kao da sam dirnuo u osinje gnijezdo.  |
Mah, to je samo HijenA... 
Osim toga, što god bilo, ti tome nisi kriv. Zanimalo te zašto si izgubio bodove, odgovor si dobio (možda malo predetaljan za tvoj ukus, ali tako je to često na ovom Forumu: ). Što se dalje događa u diskusiji, možeš čitati ako te zanima, možeš odmahnuti rukom, možeš i sudjelovati ako želiš, ali u svakom slučaju, nisi odgovoran za ono što drugi pišu. Mi smo svi odrasli ljudi – ili bar tako, s različitim uspjesima, glumimo. 
|
|
| [Vrh] |
|
Vjeko
Forumaš(ica)

Pridružen/a: 26. 10. 2004. (17:33:06)
Postovi: (39)16
Spol: 
|
 Postano: 8:04 pet, 17. 12. 2004 Naslov: Postano: 8:04 pet, 17. 12. 2004 Naslov: |
    |
|
|
[quote="veky"]BTW što ti je to na čelu? :-k
[/quote]
To je moja varijanta riječi "Pseudo". A to što je došlo do kovanice Pseudo-Vjeko korijen ima u UUR-u i pripremama za kolokvij iz istoga. Detaljnije objašnjenje slijedi, ali ne sad ujutro, kad sam na net doletio nakratko.
[quote="veky"]odgovor si dobio (možda malo predetaljan za tvoj ukus, ali tako je to često na ovom Forumu: ).
[/quote]
Takvo što ne postoji. Ili ako i postoji, u svakom je slučaju bolje od dvije krajnosti. Nemam ništa protiv da su svi odgovori na moja pitanja takvi.
Ali da nema takvih žestokih diskusija život bi bio dosadan, ne?
| veky (napisa): | BTW što ti je to na čelu? 
|
To je moja varijanta riječi "Pseudo". A to što je došlo do kovanice Pseudo-Vjeko korijen ima u UUR-u i pripremama za kolokvij iz istoga. Detaljnije objašnjenje slijedi, ali ne sad ujutro, kad sam na net doletio nakratko.
| veky (napisa): | odgovor si dobio (možda malo predetaljan za tvoj ukus, ali tako je to često na ovom Forumu: ).
|
Takvo što ne postoji. Ili ako i postoji, u svakom je slučaju bolje od dvije krajnosti. Nemam ništa protiv da su svi odgovori na moja pitanja takvi.
Ali da nema takvih žestokih diskusija život bi bio dosadan, ne?
_________________  Mir i dug život! 
 Živi dugo i uspješno!  |
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
|















