| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Markec
Forumaš(ica)

Pridružen/a: 20. 02. 2003. (14:49:45)
Postovi: (134)16
Spol: 
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 21:57 ned, 5. 12. 2004 Naslov: Re: Zadatak Lin. operator (s matricama) Postano: 21:57 ned, 5. 12. 2004 Naslov: Re: Zadatak Lin. operator (s matricama) |
    |
|
|
(prvi dio je točan)
[quote="Markec"]Trebamo odrediti matricu od A u kanonskoj bazi od M2([b]R[/b])[size=18][color=red]???[/color][/size][/quote]
Kanonska baza od M_2(|R) je (E11,E12,E21,E22) , gdje je Eij matrica koja na (i,j)-mjestu ima jedinicu, ostalo nule. Npr. E12=[0 1//0 0] .
Tvoje je da vidiš kako A preslikava E11 , E12 , E21 i E22 , te rezultate zapišeš natrag u toj bazi (efektivno, samo pročitaš komponente matrice po recima), i to potrpaš u stupce matrice A_Bk koju želiš dobiti.
Ako ja nisam negdje zeznuo, trebaš dobiti
A_Bk=[1 -1 0 0//-1 1 2 0//1 0 -1 -1//-1 0 2 1] .
Kao što vidiš, traženu matricu možeš dobiti i po recima, tako da jednostavno čitaš komponente tipične slike od A , odnosno u njima koeficijente uz a,b,c,d (npr. a-b => 1,-1,0,0 ).
(prvi dio je točan)
| Markec (napisa): | | Trebamo odrediti matricu od A u kanonskoj bazi od M2(R)??? |
Kanonska baza od M_2(|R) je (E11,E12,E21,E22) , gdje je Eij matrica koja na (i,j)-mjestu ima jedinicu, ostalo nule. Npr. E12=[0 1//0 0] .
Tvoje je da vidiš kako A preslikava E11 , E12 , E21 i E22 , te rezultate zapišeš natrag u toj bazi (efektivno, samo pročitaš komponente matrice po recima), i to potrpaš u stupce matrice A_Bk koju želiš dobiti.
Ako ja nisam negdje zeznuo, trebaš dobiti
A_Bk=[1 -1 0 0//-1 1 2 0//1 0 -1 -1//-1 0 2 1] .
Kao što vidiš, traženu matricu možeš dobiti i po recima, tako da jednostavno čitaš komponente tipične slike od A , odnosno u njima koeficijente uz a,b,c,d (npr. a-b ⇒ 1,-1,0,0 ).
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 12:21 uto, 7. 12. 2004 Naslov: Re: Zadatak Lin. operator (s matricama) Postano: 12:21 uto, 7. 12. 2004 Naslov: Re: Zadatak Lin. operator (s matricama) |
    |
|
|
[quote="veky"](prvi dio je točan)
[quote="Markec"]Trebamo odrediti matricu od A u kanonskoj bazi od M2([b]R[/b])[size=18][color=red]???[/color][/size][/quote]
Kanonska baza od M_2(|R) je (E11,E12,E21,E22) , gdje je Eij matrica koja na (i,j)-mjestu ima jedinicu, ostalo nule. Npr. E12=[0 1//0 0] .
Tvoje je da vidiš kako A preslikava E11 , E12 , E21 i E22 , te rezultate zapišeš natrag u toj bazi (efektivno, samo pročitaš komponente matrice po recima), i to potrpaš u stupce matrice A_Bk koju želiš dobiti.
Ako ja nisam negdje zeznuo, trebaš dobiti
A_Bk=[1 -1 0 0//-1 1 2 0//1 0 -1 -1//-1 0 2 1] .
Kao što vidiš, traženu matricu možeš dobiti i po recima, tako da jednostavno čitaš komponente tipične slike od A , odnosno u njima koeficijente uz a,b,c,d (npr. a-b => 1,-1,0,0 ).[/quote]
jel ti se da raspisati?! ajd pliz. tejnks :)
| veky (napisa): | (prvi dio je točan)
| Markec (napisa): | | Trebamo odrediti matricu od A u kanonskoj bazi od M2(R)??? |
Kanonska baza od M_2(|R) je (E11,E12,E21,E22) , gdje je Eij matrica koja na (i,j)-mjestu ima jedinicu, ostalo nule. Npr. E12=[0 1//0 0] .
Tvoje je da vidiš kako A preslikava E11 , E12 , E21 i E22 , te rezultate zapišeš natrag u toj bazi (efektivno, samo pročitaš komponente matrice po recima), i to potrpaš u stupce matrice A_Bk koju želiš dobiti.
Ako ja nisam negdje zeznuo, trebaš dobiti
A_Bk=[1 -1 0 0//-1 1 2 0//1 0 -1 -1//-1 0 2 1] .
Kao što vidiš, traženu matricu možeš dobiti i po recima, tako da jednostavno čitaš komponente tipične slike od A , odnosno u njima koeficijente uz a,b,c,d (npr. a-b ⇒ 1,-1,0,0 ). |
jel ti se da raspisati?! ajd pliz. tejnks 
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 14:38 uto, 7. 12. 2004 Naslov: Re: Zadatak Lin. operator (s matricama) Postano: 14:38 uto, 7. 12. 2004 Naslov: Re: Zadatak Lin. operator (s matricama) |
    |
|
|
[quote="HijenA"]jel ti se da raspisati?! ajd pliz. tejnks :)[/quote]
_Što_ raspisati?
Ovo zadnje?
Well, OP reče:
[latex]A( \left[ \begin{array}{cc} a & b \\
c & d \end{array} \right] ) = \left[ \begin{array}{cc} a-b & -a+b+2c \\
a-c-d & -a+2c+d \end{array} \right][/latex]
Na prvom mjestu (11) slike stoji a-b=1*a+(-1)*b+0*c+0*d . Dakle u prvi redak pišeš 1,-1,0,0 . Na drugom mjestu (12) stoji -a+b+2c , so u drugi redak ide -1,1,2,0 . Na trećem (21) stoji a-c-d , so treći redak tražene matrice je 1,0,-1,-1 . I zadnji redak je -a+2c+d --> -1,0,2,1 .
To si mislio?
| HijenA (napisa): | jel ti se da raspisati?! ajd pliz. tejnks  |
_Što_ raspisati?
Ovo zadnje?
Well, OP reče:
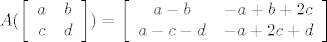
Na prvom mjestu (11) slike stoji a-b=1*a+(-1)*b+0*c+0*d . Dakle u prvi redak pišeš 1,-1,0,0 . Na drugom mjestu (12) stoji -a+b+2c , so u drugi redak ide -1,1,2,0 . Na trećem (21) stoji a-c-d , so treći redak tražene matrice je 1,0,-1,-1 . I zadnji redak je -a+2c+d → -1,0,2,1 .
To si mislio?
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 17:16 uto, 7. 12. 2004 Naslov: Re: Zadatak Lin. operator (s matricama) Postano: 17:16 uto, 7. 12. 2004 Naslov: Re: Zadatak Lin. operator (s matricama) |
    |
|
|
[quote="veky"][quote="HijenA"]jel ti se da raspisati?! ajd pliz. tejnks :)[/quote]
_Što_ raspisati?
Ovo zadnje?
Well, OP reče:
[latex]A( \left[ \begin{array}{cc} a & b \\
c & d \end{array} \right] ) = \left[ \begin{array}{cc} a-b & -a+b+2c \\
a-c-d & -a+2c+d \end{array} \right][/latex]
Na prvom mjestu (11) slike stoji a-b=1*a+(-1)*b+0*c+0*d . Dakle u prvi redak pišeš 1,-1,0,0 . Na drugom mjestu (12) stoji -a+b+2c , so u drugi redak ide -1,1,2,0 . Na trećem (21) stoji a-c-d , so treći redak tražene matrice je 1,0,-1,-1 . I zadnji redak je -a+2c+d --> -1,0,2,1 .
To si mislio?[/quote]
upravo to. hvala :D
| veky (napisa): | | HijenA (napisa): | jel ti se da raspisati?! ajd pliz. tejnks  |
_Što_ raspisati?
Ovo zadnje?
Well, OP reče:
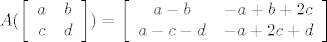
Na prvom mjestu (11) slike stoji a-b=1*a+(-1)*b+0*c+0*d . Dakle u prvi redak pišeš 1,-1,0,0 . Na drugom mjestu (12) stoji -a+b+2c , so u drugi redak ide -1,1,2,0 . Na trećem (21) stoji a-c-d , so treći redak tražene matrice je 1,0,-1,-1 . I zadnji redak je -a+2c+d → -1,0,2,1 .
To si mislio? |
upravo to. hvala 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
 Postano: 5:30 čet, 20. 1. 2005 Naslov: Postano: 5:30 čet, 20. 1. 2005 Naslov: |
    |
|
|
Opcenito, skup izvodnica za Im je skup slika vektora (bilo koje) baze domene pa se nadju te slike i dobiveni skup reducira na linearno nezavisan. U konkretnom zadatku, nadju se slike 4 matrice koje cine bazu i onda se ukloni jedna koja se moze izraziti kao lin. kombinacija ostalih (moze se primijeniti cinjenica da ce se jedan dati prikazati pomocu prethodnih).
Dakle, neka je f s V u W linearni operator i (e1,..., en) baza od V.
Medju vektorima f(e1),...,f(en) postoji baza za Im f pa se primijeni redukcija skupa izvodnica (za Im f) do baze.
Opcenito, skup izvodnica za Im je skup slika vektora (bilo koje) baze domene pa se nadju te slike i dobiveni skup reducira na linearno nezavisan. U konkretnom zadatku, nadju se slike 4 matrice koje cine bazu i onda se ukloni jedna koja se moze izraziti kao lin. kombinacija ostalih (moze se primijeniti cinjenica da ce se jedan dati prikazati pomocu prethodnih).
Dakle, neka je f s V u W linearni operator i (e1,..., en) baza od V.
Medju vektorima f(e1),...,f(en) postoji baza za Im f pa se primijeni redukcija skupa izvodnica (za Im f) do baze.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|







