| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
defar
Forumaš(ica)
Pridružen/a: 19. 01. 2004. (01:37:19)
Postovi: (152)16
|
 Postano: 20:48 čet, 20. 1. 2005 Naslov: diferencijalna_jednadzba_savjeti |
    |
|
|
zbilja bi trebala rijesiti sljedecu dif. jednadzbu:
x^2+y^2y'-xyy'=0 , a do sad mi nije poslo za rukom, i cini se da sam iscrpila sve ideje.
doduse, ja bas i nisam vjesta u tome, pa mozda nesto bitno ne vidim.
daklem, jednadzba je oblika x^2dx+(y^2-xy)dy=0
tj.
dy/dx=x^2/(xy-y^2)
pa je dx/dy=(xy-y^2)/x^2= y/x - y^2/x^2
probala sam se dokopat' rjesenja supstitucijom u(y)=x(y)/y , medjutim
to dovodi do toga da se mora (po u) integrirati funkcija
u^2/(1-u-u^3) , a ja to ne znam. uopce ne vidim sto bi pametno napravila. cini se da nazivnik ima kompleksne nultocke - daklem rastav na parcijalne razlomke otpada.
nadalje, jednadzba nije egzaktna, derivacija prve koordinatne fje dif. forme po drugoj var. je 0, a druge po prvoj -y.
ne mogu meni poznatim tehnikama niti nekakvim odokativnim napipavanjem naci lagrangeov multiplikator.
ako ima zainteresiranih, savjete svake vrste prihvacam :D
zbilja bi trebala rijesiti sljedecu dif. jednadzbu:
x^2+y^2y'-xyy'=0 , a do sad mi nije poslo za rukom, i cini se da sam iscrpila sve ideje.
doduse, ja bas i nisam vjesta u tome, pa mozda nesto bitno ne vidim.
daklem, jednadzba je oblika x^2dx+(y^2-xy)dy=0
tj.
dy/dx=x^2/(xy-y^2)
pa je dx/dy=(xy-y^2)/x^2= y/x - y^2/x^2
probala sam se dokopat' rjesenja supstitucijom u(y)=x(y)/y , medjutim
to dovodi do toga da se mora (po u) integrirati funkcija
u^2/(1-u-u^3) , a ja to ne znam. uopce ne vidim sto bi pametno napravila. cini se da nazivnik ima kompleksne nultocke - daklem rastav na parcijalne razlomke otpada.
nadalje, jednadzba nije egzaktna, derivacija prve koordinatne fje dif. forme po drugoj var. je 0, a druge po prvoj -y.
ne mogu meni poznatim tehnikama niti nekakvim odokativnim napipavanjem naci lagrangeov multiplikator.
ako ima zainteresiranih, savjete svake vrste prihvacam 
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)
Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
| Postano: 0:28 pet, 21. 1. 2005 Naslov: Re: diferencijalna_jednadzba_savjeti |
|
|
|
[quote="defar"]zbilja bi trebala rijesiti sljedecu dif. jednadzbu:
probala sam se dokopat' rjesenja supstitucijom u(y)=x(y)/y , medjutim
to dovodi do toga da se mora (po u) integrirati funkcija
u^2/(1-u-u^3) , a ja to ne znam. uopce ne vidim sto bi pametno napravila.
[/quote]
Jednadzba je homogena, sto znaci da odmah mozes uvrstiti supstituciju z(x)=y(x)/x.
Mene to dovodi do toga da se treba po z integrirati (z - z^2)/(1 - z^2 + z^3), a kao integral toga Mathematica navodi neku bolestinu, i nisam siguran moze li se ta funkcija integrirati elementarnim metodama.
(Svojom supstitucijom ti dobivas nesto slicno i prica je ista...)
[quote="defar"]
cini se da nazivnik ima kompleksne nultocke - daklem rastav na parcijalne razlomke otpada.
[/quote]
Svaki polinom treceg (i svakog drugog neparnog) stupnja s realnim koeficijentima ima realne nultocke (limesi u plus u minus beskonacno su mu razliciti, jedan plus, a drugi minus beskonacno, pa negdje mora prolaziti kroz nulu), samo je problem sto je (jedina) realna nultocka od 1-u-u^3 jednaka
[latex]
u=-(\frac{2}{3(9+\sqrt{93})})^\frac{1}{3}+\frac{(\frac{1}{2}(9+\sqrt{93})^\frac{1}{3})}{3^\frac{2}{3}}
[/latex]...
Mathematica inace za samo rjesenje jednadzbe kaze [i]The equations appear to involve the variables to be solved for in an essentially non-algebraic way.[/i]
Tako da ja sumnjam da se moze nesto pametno napraviti s tom jednadzbom :(
| defar (napisa): | zbilja bi trebala rijesiti sljedecu dif. jednadzbu:
probala sam se dokopat' rjesenja supstitucijom u(y)=x(y)/y , medjutim
to dovodi do toga da se mora (po u) integrirati funkcija
u^2/(1-u-u^3) , a ja to ne znam. uopce ne vidim sto bi pametno napravila.
|
Jednadzba je homogena, sto znaci da odmah mozes uvrstiti supstituciju z(x)=y(x)/x.
Mene to dovodi do toga da se treba po z integrirati (z - z^2)/(1 - z^2 + z^3), a kao integral toga Mathematica navodi neku bolestinu, i nisam siguran moze li se ta funkcija integrirati elementarnim metodama.
(Svojom supstitucijom ti dobivas nesto slicno i prica je ista...)
| defar (napisa): |
cini se da nazivnik ima kompleksne nultocke - daklem rastav na parcijalne razlomke otpada.
|
Svaki polinom treceg (i svakog drugog neparnog) stupnja s realnim koeficijentima ima realne nultocke (limesi u plus u minus beskonacno su mu razliciti, jedan plus, a drugi minus beskonacno, pa negdje mora prolaziti kroz nulu), samo je problem sto je (jedina) realna nultocka od 1-u-u^3 jednaka
 ...
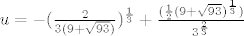Mathematica inace za samo rjesenje jednadzbe kaze The equations appear to involve the variables to be solved for in an essentially non-algebraic way.
Tako da ja sumnjam da se moze nesto pametno napraviti s tom jednadzbom 
|
|
| [Vrh] |
|
defar
Forumaš(ica)
Pridružen/a: 19. 01. 2004. (01:37:19)
Postovi: (152)16
|
| Postano: 0:56 pet, 21. 1. 2005 Naslov: Re: diferencijalna_jednadzba_savjeti |
|
|
|
[quote="Tonci"]
Svaki polinom treceg (i svakog drugog neparnog) stupnja s realnim koeficijentima ima realne nultocke (limesi u plus u minus beskonacno su mu razliciti, jedan plus, a drugi minus beskonacno, pa negdje mora prolaziti kroz nulu)
[/quote]
ah, da, zbilja. :oops: ja vidila "ruzan" polinom, koji ne mogu odokativno faktorizirat', pa ga odmah otpisala...
[quote="Tonci"]
Mene to dovodi do toga da se treba po z integrirati (z - z^2)/(1 - z^2 + z^3), a kao integral toga Mathematica navodi neku bolestinu, i nisam siguran moze li se ta funkcija integrirati elementarnim metodama.
(Svojom supstitucijom ti dobivas nesto slicno i prica je ista...)
[/quote]
znaci, ipak nije tako pitoma? :(
no, hvala puno na trudu, cak si i mathematicu konzultirao! :)
| Tonci (napisa): |
Svaki polinom treceg (i svakog drugog neparnog) stupnja s realnim koeficijentima ima realne nultocke (limesi u plus u minus beskonacno su mu razliciti, jedan plus, a drugi minus beskonacno, pa negdje mora prolaziti kroz nulu)
|
ah, da, zbilja.  ja vidila "ruzan" polinom, koji ne mogu odokativno faktorizirat', pa ga odmah otpisala...
| Tonci (napisa): |
Mene to dovodi do toga da se treba po z integrirati (z - z^2)/(1 - z^2 + z^3), a kao integral toga Mathematica navodi neku bolestinu, i nisam siguran moze li se ta funkcija integrirati elementarnim metodama.
(Svojom supstitucijom ti dobivas nesto slicno i prica je ista...)
|
znaci, ipak nije tako pitoma?
no, hvala puno na trudu, cak si i mathematicu konzultirao! 
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|
|
| [Vrh] |
|
veky
Forumaš(ica)
Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
| Postano: 17:07 pet, 21. 1. 2005 Naslov: Re: diferencijalna_jednadzba_savjeti |
|
|
|
[quote="Tonci"]
Mene to dovodi do toga da se treba po z integrirati (z - z^2)/(1 - z^2 + z^3), a kao integral toga Mathematica navodi neku bolestinu, i nisam siguran moze li se ta funkcija integrirati elementarnim metodama.[/quote]
Naravno da može. To je integral racionalne funkcije. Čak štoviše, nazivnik je 3. stupnja, i jedna nultočka je realna a ostale dvije konjugirano kompleksne, pa se integrand može zapisati rastavom na parcijalne razlomke kao A/(z-z0)+(Bz+C)/(z^2+alfa*z+beta) , što se onda lako riješi. Jedini je problem što alfa i beta ovise o z0 , a z0 je užasno kompliciran (iako elementarno izraziv).
Pouka: ne miješati "elementarno" i "lagano". ;-)
[quote]Svaki polinom treceg (i svakog drugog neparnog) stupnja s realnim koeficijentima ima realne nultocke[/quote]
Bar jednu, that is. :-)
[quote]Mathematica inace za samo rjesenje jednadzbe kaze [i]The equations appear to involve the variables to be solved for in an essentially non-algebraic way.[/i]
Tako da ja sumnjam da se moze nesto pametno napraviti s tom jednadzbom :([/quote]
Mathematica zna biti blesava ponekad... lijepo kaže da se radi o RootSumu, Normal ga čak rastavi na Rootove, i onda Cubics nikako da je nagovori da stvarno raspiše kako izgledaju ti korijeni. No dobro, nije da bi se time dobilo nešto jednostavno (linearne kombinacije logaritama skoro-pa rješenjâ gornje jednadžbe trećeg stupnja), ali svejedno sam očekivao da Mma pokaže malo manje lijenosti. :-o :-)
| Tonci (napisa): |
Mene to dovodi do toga da se treba po z integrirati (z - z^2)/(1 - z^2 + z^3), a kao integral toga Mathematica navodi neku bolestinu, i nisam siguran moze li se ta funkcija integrirati elementarnim metodama. |
Naravno da može. To je integral racionalne funkcije. Čak štoviše, nazivnik je 3. stupnja, i jedna nultočka je realna a ostale dvije konjugirano kompleksne, pa se integrand može zapisati rastavom na parcijalne razlomke kao A/(z-z0)+(Bz+C)/(z^2+alfa*z+beta) , što se onda lako riješi. Jedini je problem što alfa i beta ovise o z0 , a z0 je užasno kompliciran (iako elementarno izraziv).
Pouka: ne miješati "elementarno" i "lagano". 
| Citat: | | Svaki polinom treceg (i svakog drugog neparnog) stupnja s realnim koeficijentima ima realne nultocke |
Bar jednu, that is.
| Citat: | Mathematica inace za samo rjesenje jednadzbe kaze The equations appear to involve the variables to be solved for in an essentially non-algebraic way.
Tako da ja sumnjam da se moze nesto pametno napraviti s tom jednadzbom |
Mathematica zna biti blesava ponekad... lijepo kaže da se radi o RootSumu, Normal ga čak rastavi na Rootove, i onda Cubics nikako da je nagovori da stvarno raspiše kako izgledaju ti korijeni. No dobro, nije da bi se time dobilo nešto jednostavno (linearne kombinacije logaritama skoro-pa rješenjâ gornje jednadžbe trećeg stupnja), ali svejedno sam očekivao da Mma pokaže malo manje lijenosti. 
|
|
| [Vrh] |
|
Edo
Forumaš(ica)
Pridružen/a: 09. 02. 2004. (23:03:41)
Postovi: (6C)16
|
| Postano: 14:45 sub, 22. 1. 2005 Naslov: |
|
|
|
Mozda ja mogu dati jedan generalni savjet za ODJ. Dakle, prije puno, puno godina (prije nego su se rodili vasi ocevi, a mozda i djedovi) jedan je njemacki matematicar imenom E.Kamke sastavio tablice rjesenja za ODJ svih mogucih tipova. Knjiga je izdana u bezbroj izdanja i jedno od njih se moze naci u nasoj knjiznici : Kamke, E. (1961): "Differentialgleichungen-Lösungsmethoden und Lösungen, 1. Gewöhnliche Differentialgleichungen", Akad Verl. Ges. Geest & Portig K.G., Leipzig, 7th edition.
Postoje i ruski i engelski prijevod. Ako imate u rukama ODJ koja se moze pjesice rijesiti, naci cete je tamo. Sanse da jednadzba nije tabelirana u Kamkeu, a da se rjesenje moze izraziti, bilo eksplicitno bilo implicitno preko znanih nam elementarnih i specijalnih funkcija, tako su male da medju ljudima od struke vrijedi pravilo da ono sto nije u Kamkeu treba rjesavati numericki.
Knjiga je ogromna i u njoj se ponekad teze snaci, ali je puno pouzdanija od Mathematice, premda se oni pozivaju na Kamkea.
Mozda ja mogu dati jedan generalni savjet za ODJ. Dakle, prije puno, puno godina (prije nego su se rodili vasi ocevi, a mozda i djedovi) jedan je njemacki matematicar imenom E.Kamke sastavio tablice rjesenja za ODJ svih mogucih tipova. Knjiga je izdana u bezbroj izdanja i jedno od njih se moze naci u nasoj knjiznici : Kamke, E. (1961): "Differentialgleichungen-Lösungsmethoden und Lösungen, 1. Gewöhnliche Differentialgleichungen", Akad Verl. Ges. Geest & Portig K.G., Leipzig, 7th edition.
Postoje i ruski i engelski prijevod. Ako imate u rukama ODJ koja se moze pjesice rijesiti, naci cete je tamo. Sanse da jednadzba nije tabelirana u Kamkeu, a da se rjesenje moze izraziti, bilo eksplicitno bilo implicitno preko znanih nam elementarnih i specijalnih funkcija, tako su male da medju ljudima od struke vrijedi pravilo da ono sto nije u Kamkeu treba rjesavati numericki.
Knjiga je ogromna i u njoj se ponekad teze snaci, ali je puno pouzdanija od Mathematice, premda se oni pozivaju na Kamkea.
|
|
| [Vrh] |
|
veky
Forumaš(ica)
Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
| Postano: 18:13 sub, 22. 1. 2005 Naslov: |
|
|
|
[quote="Edo"]Knjiga je ogromna i u njoj se ponekad teze snaci, ali je puno pouzdanija od Mathematice, premda se oni pozivaju na Kamkea.[/quote]
Pouzdanija? :shock:
Možeš navesti primjer ODJ koja je u Kamkeu, a Mma je ne može riješiti? (Primijeti da ova gornja nije takva... to je stvarno jednostavni integral racionalne funkcije. To što su nultočke nazivnika grozomorne, nije stvar oblika diferencijalne jednadžbe, i u tome ti IMHO neće ni Kamke pomoći. : )
| Edo (napisa): | | Knjiga je ogromna i u njoj se ponekad teze snaci, ali je puno pouzdanija od Mathematice, premda se oni pozivaju na Kamkea. |
Pouzdanija? 
Možeš navesti primjer ODJ koja je u Kamkeu, a Mma je ne može riješiti? (Primijeti da ova gornja nije takva... to je stvarno jednostavni integral racionalne funkcije. To što su nultočke nazivnika grozomorne, nije stvar oblika diferencijalne jednadžbe, i u tome ti IMHO neće ni Kamke pomoći. : )
|
|
| [Vrh] |
|
defar
Forumaš(ica)
Pridružen/a: 19. 01. 2004. (01:37:19)
Postovi: (152)16
|
| Postano: 18:32 sub, 22. 1. 2005 Naslov: |
|
|
|
[quote="Edo"] Kamke, E. (1961): "Differentialgleichungen-Lösungsmethoden und Lösungen, 1. Gewöhnliche Differentialgleichungen", Akad Verl. Ges. Geest & Portig K.G., Leipzig, 7th edition.
Postoje i ruski i engelski prijevod.[/quote]
hah, zvuci tako romanticno :D
hvala! spremljeno u "good to know"(a vjerovatno odem i vidit kako to cudo izgleda) iako ni bronsteina nikad bas nisam prihvatila...
a iz daljnje rasprave se povlacim, jer i ne znam mnogo niti o dif. jednadzbama, niti o tome kako Mathematica ustvari funkcionira...
| Edo (napisa): | Kamke, E. (1961): "Differentialgleichungen-Lösungsmethoden und Lösungen, 1. Gewöhnliche Differentialgleichungen", Akad Verl. Ges. Geest & Portig K.G., Leipzig, 7th edition.
Postoje i ruski i engelski prijevod. |
hah, zvuci tako romanticno
hvala! spremljeno u "good to know"(a vjerovatno odem i vidit kako to cudo izgleda) iako ni bronsteina nikad bas nisam prihvatila...
a iz daljnje rasprave se povlacim, jer i ne znam mnogo niti o dif. jednadzbama, niti o tome kako Mathematica ustvari funkcionira...
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|
|
| [Vrh] |
|
Edo
Forumaš(ica)
Pridružen/a: 09. 02. 2004. (23:03:41)
Postovi: (6C)16
|
| Postano: 0:27 ned, 23. 1. 2005 Naslov: |
|
|
|
[quote="veky"]Pouzdanija? :shock:
Možeš navesti primjer ODJ koja je u Kamkeu, a Mma je ne može riješiti? (Primijeti da ova gornja nije takva... to je stvarno jednostavni integral racionalne funkcije. To što su nultočke nazivnika grozomorne, nije stvar oblika diferencijalne jednadžbe, i u tome ti IMHO neće ni Kamke pomoći. : )[/quote]
Puno pouzdanija je mozda pretjerano, ali kad sam se zadnji put bavio tom problematikom, prije nekih 5-6 godina, mathematica i maple mi nisu pomogli, za razliku od Kamkea. Da bi se prisjetio jednadzbe, morao bi kopati po papirima, ali do nje smo dosli separacijom varijabli za Schrodingera u vanjstini paraboloida ili konusa (ne sjecam se vise). Dobila se nekakva ODJ s regularnim singularitetom Fuchsovog tipa, a rjesenje joj je imalo neke veze s hipergeometrijskim f-jama. Mozda je Mathematica od tada evoluirala, ali tesko mi je vjerovati da bi netko zbilja u svoj software ugradjivao sve one preverzije koje je gospodin Kamke desetljecima sakupljao.
S PDJ je situacija bitno gora ili je meni tu lakse naci feler jer sam tu kod kuce.
Primjer kad se maple sasvim raspao, koji mi je u svjezijem sjecanju je vezan uz hiperbolicke PDJ 1. reda i metodu karakteristika. Probao sam rijesiti Burgersovu jednadzbu s pocetnim uvjetom koji nije monoton i maple nije skuzio shock val. Jednostavno, maple i mathematica su solidni proizvodi opce prakse, ali nje za ocekivati da ce rijesiti vrlo specijalne probleme, npr. izabrati entropijsko rjesenje u mnostvu rjesenja Burgersove jednadzbe. Za to nisu ni stvoreni.
| veky (napisa): | Pouzdanija?
Možeš navesti primjer ODJ koja je u Kamkeu, a Mma je ne može riješiti? (Primijeti da ova gornja nije takva... to je stvarno jednostavni integral racionalne funkcije. To što su nultočke nazivnika grozomorne, nije stvar oblika diferencijalne jednadžbe, i u tome ti IMHO neće ni Kamke pomoći. : ) |
Puno pouzdanija je mozda pretjerano, ali kad sam se zadnji put bavio tom problematikom, prije nekih 5-6 godina, mathematica i maple mi nisu pomogli, za razliku od Kamkea. Da bi se prisjetio jednadzbe, morao bi kopati po papirima, ali do nje smo dosli separacijom varijabli za Schrodingera u vanjstini paraboloida ili konusa (ne sjecam se vise). Dobila se nekakva ODJ s regularnim singularitetom Fuchsovog tipa, a rjesenje joj je imalo neke veze s hipergeometrijskim f-jama. Mozda je Mathematica od tada evoluirala, ali tesko mi je vjerovati da bi netko zbilja u svoj software ugradjivao sve one preverzije koje je gospodin Kamke desetljecima sakupljao.
S PDJ je situacija bitno gora ili je meni tu lakse naci feler jer sam tu kod kuce.
Primjer kad se maple sasvim raspao, koji mi je u svjezijem sjecanju je vezan uz hiperbolicke PDJ 1. reda i metodu karakteristika. Probao sam rijesiti Burgersovu jednadzbu s pocetnim uvjetom koji nije monoton i maple nije skuzio shock val. Jednostavno, maple i mathematica su solidni proizvodi opce prakse, ali nje za ocekivati da ce rijesiti vrlo specijalne probleme, npr. izabrati entropijsko rjesenje u mnostvu rjesenja Burgersove jednadzbe. Za to nisu ni stvoreni.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja
Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
|
homogena afaik nije, a nije ni linearna ni bernoullijeva(?). Ideje?
