|
Rješenje je
[latex]\displaystyle\frac{2l}{\pi M}+\displaystyle\frac{2l}{\pi L}-\displaystyle\frac{l^2}{\pi ML}[/latex]
tj. P(klasični Buffon)+P(klasični buffon)-P(presjek)
[quote]Mislio sam da je trazeni skup kruznica polumjera l/2 oko tocke u kojoj se sijeku cetiri stranice dva pravokutnika, no unutar te kruznice igla moze pasti t.d. ona ne sijece oba pravokutnika.[/quote]
Zato i ne možeš tako jednostavno, nego i kad računaš vjerojatnost presjeka moraš uzeti u obzir "smjer igle" (određen nekim kutom).
Dakle, izračunajmo vjerojatnost da igla siječe i neki vertikalni i neki horizontalni pravac. Neka igla zatvara kut [latex]\varphi\in\left\langle 0,\frac{\pi}{2}\right\rangle[/latex] s x-osi (zbog simetrije je dosta gledati takve kutove) i neka je (x,y) njeno središte.
Igla siječe i vertikalni i horizontalni pravac akko je (x,y) unutar nekog pravokutnika sa središtem u čvoru mreže i stranicama duljina [latex]l\cos\varphi[/latex], [latex]l\sin\varphi[/latex].
Vjerojatnost je
[latex]\displaystyle\frac{1}{\frac{\pi}{2}\cdot ML}\displaystyle\int_{0}^{\pi/2}l^2 \cos\varphi\sin\varphi\,d\varphi=\displaystyle\frac{l^2}{\pi ML}[/latex]
Čini se da se ta generalizacija zove Buffon-Laplace-ov problem:
http://mathworld.wolfram.com/Buffon-LaplaceNeedleProblem.html
Rješenje je
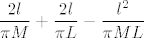
tj. P(klasični Buffon)+P(klasični buffon)-P(presjek)
| Citat: | | Mislio sam da je trazeni skup kruznica polumjera l/2 oko tocke u kojoj se sijeku cetiri stranice dva pravokutnika, no unutar te kruznice igla moze pasti t.d. ona ne sijece oba pravokutnika. |
Zato i ne možeš tako jednostavno, nego i kad računaš vjerojatnost presjeka moraš uzeti u obzir "smjer igle" (određen nekim kutom).
Dakle, izračunajmo vjerojatnost da igla siječe i neki vertikalni i neki horizontalni pravac. Neka igla zatvara kut 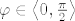 s x-osi (zbog simetrije je dosta gledati takve kutove) i neka je (x,y) njeno središte.
Igla siječe i vertikalni i horizontalni pravac akko je (x,y) unutar nekog pravokutnika sa središtem u čvoru mreže i stranicama duljina  ,  .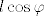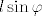
Vjerojatnost je
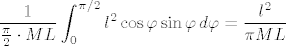
Čini se da se ta generalizacija zove Buffon-Laplace-ov problem:
http://mathworld.wolfram.com/Buffon-LaplaceNeedleProblem.html
|
