| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
defar
Forumaš(ica)
Pridružen/a: 19. 01. 2004. (01:37:19)
Postovi: (152)16
|
 Postano: 21:07 uto, 8. 2. 2005 Naslov: |
    |
|
|
pa...mozda bi se to moglo ovako nekako pobrojat:
najvise sto mozes stavit' u prve dvije kutije je k kuglica. ovako:
k k 1
onda mozes u zadnju kutiju stavit 2 kuglice (onda moras ili iz prve ili iz druge tu jos jednu premjestit):
k-1 k 2 ili k k-1 2
onda, ako u trecu kutiju stavis tri , mozes ovako:
k-2 k 3
k-1 k-1 3
k k-2 3
ako je u zadnjoj kutiji x kuglica, moras ih iz prve uzet' a, a iz druge b t.d.
a+b=x-1, a to se moze na (x-1)+2=x+1 nacina.
pa ukupno ima: 1+2+3+...+(k+1)=(k+1)(k+2)/2 nacina razmjestaja.
ako kutije medjusobno razlikujes(?).
pa...mozda bi se to moglo ovako nekako pobrojat:
najvise sto mozes stavit' u prve dvije kutije je k kuglica. ovako:
k k 1
onda mozes u zadnju kutiju stavit 2 kuglice (onda moras ili iz prve ili iz druge tu jos jednu premjestit):
k-1 k 2 ili k k-1 2
onda, ako u trecu kutiju stavis tri , mozes ovako:
k-2 k 3
k-1 k-1 3
k k-2 3
ako je u zadnjoj kutiji x kuglica, moras ih iz prve uzet' a, a iz druge b t.d.
a+b=x-1, a to se moze na (x-1)+2=x+1 nacina.
pa ukupno ima: 1+2+3+...+(k+1)=(k+1)(k+2)/2 nacina razmjestaja.
ako kutije medjusobno razlikujes(?).
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo
Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)
Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
| Postano: 1:31 sri, 9. 2. 2005 Naslov: |
|
|
|
A ako se kutije [u]ne[/u] razlikuju rješenje je (ako nisam pogriješio u računu, a mislim da nisam jer sam pazio):
[latex]\displaystyle\left(\left\lfloor\frac{k}{2}\right\rfloor-\left\lfloor\frac{k}{3}\right\rfloor\right)\left(\frac{3}{2}\left(\left\lfloor\frac{k}{2}\right\rfloor+\left\lfloor\frac{k}{3}\right\rfloor\right)-k+\frac{3}{2}\right)+\\
+\displaystyle\left(\left\lfloor\frac{k+1}{2}\right\rfloor-\left\lfloor\frac{k+1}{3}\right\rfloor\right)\left(\frac{3}{2}\left(\left\lfloor\frac{k+1}{2}\right\rfloor+\left\lfloor\frac{k+1}{3}\right\rfloor\right)-k+\frac{1}{2}\right)
[/latex]
Znam da to nikoga nije zanimalo, ali, eto, kao kuriozitet... :lol:
--------
Usput, ovo razlikovanje/nerazlikovanje me podsjetilo na foru:
Na koliko načina se može m bombona podijeliti na n djece ako su bomboni svi međusobno različiti, a djeca k'o djeca...
:lol: :wink:
A ako se kutije ne razlikuju rješenje je (ako nisam pogriješio u računu, a mislim da nisam jer sam pazio):
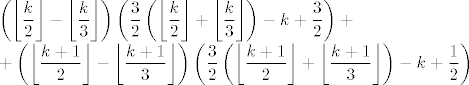
Znam da to nikoga nije zanimalo, ali, eto, kao kuriozitet... 
--------
Usput, ovo razlikovanje/nerazlikovanje me podsjetilo na foru:
Na koliko načina se može m bombona podijeliti na n djece ako su bomboni svi međusobno različiti, a djeca k'o djeca...
|
|
| [Vrh] |
|
veky
Forumaš(ica)
Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo
Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
defar
Forumaš(ica)
Pridružen/a: 19. 01. 2004. (01:37:19)
Postovi: (152)16
|
| Postano: 14:24 sri, 9. 2. 2005 Naslov: |
|
|
|
[quote="defar"]
ako je u zadnjoj kutiji x kuglica, moras ih iz prve uzet' a, a iz druge b t.d.
a+b=x-1, a to se moze na (x-1)+2=x+1 nacina.
[/quote]
hm, da, to se moze na (x-1)+1=x nacina.
onda, ako bi ih ovo tocno sve prebrojalo, odgovor bi bijo k(k+1)/2.
| defar (napisa): |
ako je u zadnjoj kutiji x kuglica, moras ih iz prve uzet' a, a iz druge b t.d.
a+b=x-1, a to se moze na (x-1)+2=x+1 nacina.
|
hm, da, to se moze na (x-1)+1=x nacina.
onda, ako bi ih ovo tocno sve prebrojalo, odgovor bi bijo k(k+1)/2.
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|
|
| [Vrh] |
|
defar
Forumaš(ica)
Pridružen/a: 19. 01. 2004. (01:37:19)
Postovi: (152)16
|
| Postano: 14:35 sri, 9. 2. 2005 Naslov: |
|
|
|
[quote="krcko"]Ako su kutije razlicite, to su cjelobrojna rjesenja jednadzbe x_1+x_2+x_3=2k+1 uz uvjet 0<=x_i<=k. Ukupno (nenegativnih) rjesenja ima (2k+1 povrh 2). Treba izbaciti ona u kojima je neka od varijabli veca od k, dakle oduzeti 3*(k+2 povrh 2).[/quote]
aha, mislio si oduzmu se svi rasporedi kod kojih je barem (k+1) rezervirano za neku od tri kutije, a preostalih 2k+1-(k+1)=k se rasporedi bilo kako - tj oduzmu se 3 puta nenegativna rj. jednadjbe x1+x2+x3=k
(njih ima (k+2 povrh 2))?
ali...mozda ih je previse tri put oduzet...najme, za k=1, tj. za tri kuglice, i za k=2, tj. pet kuglica se dobija negativno rjesenje, tj. nema rjesenja :?
| krcko (napisa): | | Ako su kutije razlicite, to su cjelobrojna rjesenja jednadzbe x_1+x_2+x_3=2k+1 uz uvjet 0⇐x_i⇐k. Ukupno (nenegativnih) rjesenja ima (2k+1 povrh 2). Treba izbaciti ona u kojima je neka od varijabli veca od k, dakle oduzeti 3*(k+2 povrh 2). |
aha, mislio si oduzmu se svi rasporedi kod kojih je barem (k+1) rezervirano za neku od tri kutije, a preostalih 2k+1-(k+1)=k se rasporedi bilo kako - tj oduzmu se 3 puta nenegativna rj. jednadjbe x1+x2+x3=k
(njih ima (k+2 povrh 2))?
ali...mozda ih je previse tri put oduzet...najme, za k=1, tj. za tri kuglice, i za k=2, tj. pet kuglica se dobija negativno rjesenje, tj. nema rjesenja 
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo
Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
| Postano: 19:11 sri, 9. 2. 2005 Naslov: |
|
|
|
[quote="defar"]ali...mozda ih je previse tri put oduzet...najme, za k=1, tj. za tri kuglice, i za k=2, tj. pet kuglica se dobija negativno rjesenje, tj. nema rjesenja :?[/quote]
Ne, greska je u prvom dijelu. Ukupno rjesenja ima (2k+3 povrh 2), a ne (2k+1 povrh 2). Kad se srede moji bin. koeficijenti dobije se isto kao tvoje rjesenje :)
| defar (napisa): | | ali...mozda ih je previse tri put oduzet...najme, za k=1, tj. za tri kuglice, i za k=2, tj. pet kuglica se dobija negativno rjesenje, tj. nema rjesenja |
Ne, greska je u prvom dijelu. Ukupno rjesenja ima (2k+3 povrh 2), a ne (2k+1 povrh 2). Kad se srede moji bin. koeficijenti dobije se isto kao tvoje rjesenje 
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
defar
Forumaš(ica)
Pridružen/a: 19. 01. 2004. (01:37:19)
Postovi: (152)16
|
| Postano: 19:21 sri, 9. 2. 2005 Naslov: |
|
|
|
aha, zbilja! :)
aha, zbilja!
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|
|
| [Vrh] |
|
Gost
|
| Postano: 22:18 sri, 9. 2. 2005 Naslov: TNx |
|
|
|
[quote]hm, da, to se moze na (x-1)+1=x nacina.
onda, ako bi ih ovo tocno sve prebrojalo, odgovor bi bijo k(k+1)/2[/quote]
HVALA VAM!!! SUPER STE! Pomoglo mi je da dodjem do istog rjesenja na drugaciji nacin, problem mi je bilo pocet sa zadatkom kao i obicno!
Jos jednom tnx!
| Citat: | hm, da, to se moze na (x-1)+1=x nacina.
onda, ako bi ih ovo tocno sve prebrojalo, odgovor bi bijo k(k+1)/2 |
HVALA VAM!!! SUPER STE! Pomoglo mi je da dodjem do istog rjesenja na drugaciji nacin, problem mi je bilo pocet sa zadatkom kao i obicno!
Jos jednom tnx!
|
|
| [Vrh] |
|
defar
Forumaš(ica)
Pridružen/a: 19. 01. 2004. (01:37:19)
Postovi: (152)16
|
| Postano: 23:00 sri, 9. 2. 2005 Naslov: Re: TNx |
|
|
|
[quote="Anonymous"]
HVALA VAM!!! SUPER STE! Pomoglo mi je da dodjem do istog rjesenja na drugaciji nacin, problem mi je bilo pocet sa zadatkom kao i obicno!
Jos jednom tnx![/quote]
cini mi se da je ipak vjekovac ponovno odnio titulu najsarmantnijeg postasa na topicu :P recimo, mozes iskoristit ovaj njegov jednostavan izraz za broj rasporeda u slucaju da kutije ne razlikujes, pa vidit kako bi stvari izgledale da ispermutiras kutije :lol:
saljim se, uzivaj i dalje u kombinatorici i vidimo se na sljedecem pismenom :)
| Anonymous (napisa): |
HVALA VAM!!! SUPER STE! Pomoglo mi je da dodjem do istog rjesenja na drugaciji nacin, problem mi je bilo pocet sa zadatkom kao i obicno!
Jos jednom tnx! |
cini mi se da je ipak vjekovac ponovno odnio titulu najsarmantnijeg postasa na topicu  recimo, mozes iskoristit ovaj njegov jednostavan izraz za broj rasporeda u slucaju da kutije ne razlikujes, pa vidit kako bi stvari izgledale da ispermutiras kutije
saljim se, uzivaj i dalje u kombinatorici i vidimo se na sljedecem pismenom
_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'
|
|
| [Vrh] |
|
|
