|
[quote]1.U teoremu 25.2. kada dokazujemo da ako integral diferenc.1-forme ne ovisi po putu integracije,onda postoji glatka funkcija f ...
Zašto je dovoljno konstruirati f u slučaju kada je skup povezan ?[/quote]
Zato što je općenito otvoreni podskup od R^n unija u parovima disjunktnih povezanih otvorenih skupova (=područja) -> to su njegove [i]komponente povezanosti[/i].
Ako konstruiramo traženu funkciju f na svakom od tih područja, onda smo zapravo definirali funkciju na njihovoj uniji (tj. cijelom otvorenom skupu). Zbog disjunktnosti komponenti je ta dobivena funkcija opet glatka, parcijalne derivacije u svakoj točki su joj iste, itd. Naime, oko svake točke skupa možemo opisati kuglicu koja se cijela nalazi u jednoj komponenti, a parcijalne derivacije u toj točki ovise samo o vrijednostima funkcije na toj kuglici.
[quote]2. U dokazu Caucyevog tm.za pravokutnik kaže se da ako je y(t) PDG parametrizacija ruba pravokutnika I,tada je i ay(t) PDG parametrizacija ruba pravokutnika Ia (a je iz <0,1> i Ia je pravokut.,unutar pravokut.I.
Otkuda taj zaključak?[/quote]
Evo baš gledam interenet-verziju skripte, str. 91. i tamo je čak nacrtana sličica. Pa, mislim, to je očigledno?!
C->C, z->az je homotetija sa središtem 0 i koeficijentom a. Dakle, ako t->y(t) parametrizira rub od I, onda t->ay(t) parametrizira njegovu sliku po toj homotetiji, a to je rub od Ia. Dakle, cijela slika se stisnula a puta.
[quote]3.Primjer funkcije koja ima izolirani singluaritet i primjer funkc.koja ima singularitet koji nije izoliran.[/quote]
Izolirani singularitet u 0 ima npr. [latex]f(z)=\displaystyle\frac{1}{z}[/latex], ili npr, [latex]f(z)=\displaystyle\frac{1}{\sin z}[/latex] ili, uostalom, bilo koji primjer s vježbi.
Singularitet koji nije izoliran ima npr. [latex]f(z)=\displaystyle\frac{1}{\sin\frac{1}{z}}[/latex]
Naime, nultočke sinusa su k*pi; k€Z pa su nultočke nazivnika [latex]\frac{1}{k\pi}[/latex]; k€Z. Točka 0 je singularitet (f nije definirana u 0), ali nije izoliran. Da bi bio izoliran, trebala bi funkcija biti analitička na nekoj okolini 0, tj. na nekom kružiću K(0,r). Ali za svaki r>0 postoji k€N takav da je [latex]\frac{1}{k\pi}<r[/latex], tj. [latex]\frac{1}{k\pi}\in K(0,r)[/latex] pa f ne može biti analitička na K(0,r).
| Citat: | 1.U teoremu 25.2. kada dokazujemo da ako integral diferenc.1-forme ne ovisi po putu integracije,onda postoji glatka funkcija f ...
Zašto je dovoljno konstruirati f u slučaju kada je skup povezan ? |
Zato što je općenito otvoreni podskup od R^n unija u parovima disjunktnih povezanih otvorenih skupova (=područja) → to su njegove komponente povezanosti.
Ako konstruiramo traženu funkciju f na svakom od tih područja, onda smo zapravo definirali funkciju na njihovoj uniji (tj. cijelom otvorenom skupu). Zbog disjunktnosti komponenti je ta dobivena funkcija opet glatka, parcijalne derivacije u svakoj točki su joj iste, itd. Naime, oko svake točke skupa možemo opisati kuglicu koja se cijela nalazi u jednoj komponenti, a parcijalne derivacije u toj točki ovise samo o vrijednostima funkcije na toj kuglici.
| Citat: | 2. U dokazu Caucyevog tm.za pravokutnik kaže se da ako je y(t) PDG parametrizacija ruba pravokutnika I,tada je i ay(t) PDG parametrizacija ruba pravokutnika Ia (a je iz <0,1> i Ia je pravokut.,unutar pravokut.I.
Otkuda taj zaključak? |
Evo baš gledam interenet-verziju skripte, str. 91. i tamo je čak nacrtana sličica. Pa, mislim, to je očigledno?!
C→C, z→az je homotetija sa središtem 0 i koeficijentom a. Dakle, ako t→y(t) parametrizira rub od I, onda t→ay(t) parametrizira njegovu sliku po toj homotetiji, a to je rub od Ia. Dakle, cijela slika se stisnula a puta.
| Citat: | | 3.Primjer funkcije koja ima izolirani singluaritet i primjer funkc.koja ima singularitet koji nije izoliran. |
Izolirani singularitet u 0 ima npr. 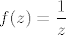 , ili npr, , ili npr, 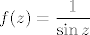 ili, uostalom, bilo koji primjer s vježbi. ili, uostalom, bilo koji primjer s vježbi.
Singularitet koji nije izoliran ima npr. 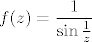
Naime, nultočke sinusa su k*pi; k€Z pa su nultočke nazivnika 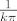 ; k€Z. Točka 0 je singularitet (f nije definirana u 0), ali nije izoliran. Da bi bio izoliran, trebala bi funkcija biti analitička na nekoj okolini 0, tj. na nekom kružiću K(0,r). Ali za svaki r>0 postoji k€N takav da je ; k€Z. Točka 0 je singularitet (f nije definirana u 0), ali nije izoliran. Da bi bio izoliran, trebala bi funkcija biti analitička na nekoj okolini 0, tj. na nekom kružiću K(0,r). Ali za svaki r>0 postoji k€N takav da je 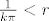 , tj. , tj. 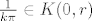 pa f ne može biti analitička na K(0,r). pa f ne može biti analitička na K(0,r).
|





