|
[quote="Pajo"][quote="veky"]
[latex]
S=( \frac{n^2 + sin \frac{n\Pi}{2}}{n^2} | n \in N) [/latex]
Kao što napisa, imaš sliku niza zadanog s a_n:=1+sin(npi/2)/n^2 . Sad imaš tri slučaja, odnosno S se rastavlja na tri skupa.
U prvom slučaju, n=2k . Tada je sin(npi/2)=sin(kpi)=0 => a_2k=1 . Supremum i infimum tog podskupa su očito 1 . 8)
U drugom slučaju, imaš n=4k+1 , k@\N . Tada je sin(npi/2)=sin(2kpi+pi/2)=sin(pi/2)=1 , pa imaš 1+1/(4k+1)^2 . To pada, pa je supremum onaj prvi, 1+1/1=2 , a infimum je limes, dakle 1 .
U trećem slučaju, imaš n=4k+3 , k@\N . Tada je ovaj sinus jednak -1 , pa ti član niza izgleda 1-1/(4k+3)^2 . To raste, pa je supremum jednak limesu, 1 , a infimum je jednak prvom članu, 1-1/3^2=8/9 .
Sve skupa, infS=min{1,1,8/9}=8/9 , a supS=max{1,2,1}=2 . Oba se naravno postižu, jedan za n=3 , drugi za n=1 .
[/quote]
Bi se moglo umjesto drugog slučaja n=4k+1 uzeti n=2k+3,a umjesto treceg slucaja n=4k+3 uzeti n=2k+1?[/quote]
Ne. Bar dok ne napišeš što je k . Podrazumijeva se (i zato i ideš s takvom supstitucijom, da dobiješ novi _niz_) da k ide po |N (ili \N=|NU{0} ). No u tom slučaju, 2k+1 i 2k+3 kupe više-manje iste brojeve (osim broja 1 ): neparne. Na primjer, 7 je i oblika 2k+1 (za k=3 ) i oblika 2k+3 (za k=2 ).
Drugi razlog je taj što ti takvi slučajevi neće puno pomoći, čak ni da čine particiju... stvar je u tome da i dalje ne znaš što ti je sin(kpi/2) . Ok, ako je k=2k+1 , imaš da je to sin(kpi+pi/2) , no i dalje to može biti i -1 i 1 (konkretno, ovdje je to (-1)^k ).
Point ovog gornjeg rastavljanja na slučajeve je upravo u tome da u svakom tom slučaju dobiješ jednostavnu konstantu za taj sin , da ti se razlomak pojednostavi.
[quote]Imamo tri slucaja,3 skupa.
prvi slucaj n=2k+1[/quote]
Gr. Gle gore... ista vrsta greške. Ne rastavljaš s obzirom na ostatke pri dijeljenju s 2 , već s 3 :!: Inače, 2k+1 i 2k+3 bi ti opet bila skoro ista stvar -- neparni brojevi; a osim toga, ne bi mogao zaključiti da je (2k+l)/3-floor((2k+l)/3) neka konstantna vrijednost (jer nije).
[quote][latex]
S=\{5 - \frac{\frac{2k+1}{3} - \lfloor \frac{2k+1}{3} \rfloor}{{2k+1}^2} | n \in N\}[/latex] [/quote]
Ovo nema baš puno smisla. Ako karakteristični element skupa ovisi o k , treba izgradnju skupa kvantificirati po k . Na primjer, ako n daje ostatak 2 pri dijeljenju s 3 , i n je prirodan broj, tada je n=3k+2 , gdje je k@\N . Dakle gornji skup (i, povrh svega, to nije S općenito :!: -- samo neki njegov podskup, jer smo uzeli samo neke n ) je S2={...| [color=red]k[/color]@\N} .
[quote]Tada je
[latex]
S=\{5 - \frac{\frac{3}{3} - \lfloor \frac{3}{3} \rfloor}{{3}^2} | n \in N\}[/latex]
za k=1 pa je supremum i infumum jednak 5.[/quote]
Slična stvar. Ne možeš sve podskupove skupa S označavati s S . :-o Ako si stavio k=1 , imaš samo jedan element od S2 , koji ti onda govori ili ne govori nešto. U ovom konkretnom slučaju, kad bi n bio djeljiv s 3 , cijeli S0 je zapravo jedank {5} , pa to i nije tolika pogreška. No u donjim slučajevima jest.
[quote]dobro je tako?[/quote]
Nije.
Ok, ajmo ispočetka. Neka je S slika nekog niza, koji označimo s (b_n)_n . Naravno, b_n:=5-(n/3-floor(n/3))/n^2 . Da bismo lakše ispitali ponašanje niza b_n , podijelit ćemo ga u tri podniza: za n=3k , n=3k+1 i n=3k+2 .
Prvi podniz: n je djeljiv s 3 . Tad je naravno n/3 cijeli broj, pa je n/3-floor(n/3)=0 . Odnosno, b_{3k}=5 , za svaki prirodni k . To je konstantan podniz, i njegova slika je samo singleton S0={5} , sa infimumom i supremumom jednakim 5 .
Drugi: n daje ostatak 1 pri dijeljenju s 3 . Dakle n=3k+1 , no iako je n prirodan broj, to znači da k može biti prirodan broj ili 0 (jasno ovo?). Dakle S1={b_{3k+1} | k@\N} . A tipični član od S1 je b_{3k+1} , takav da je "n"/3=(3k+1)/3=k+1/3 . Očito će najveće cijelo od toga biti k , pa je razlika jednaka 1/3 .
Ukupno imamo b_{3k+1}=5-(1/3)/(3k+1)^2 . Ovaj podniz raste ((s porastom k povećava se i (3k+1)^2 , pa se umanjitelj smanjuje, a budući da je umanjenik konstantan ( 5 ), b_{3k+1} se povećava)), pa je njegov infimum ujedno i minimum, ujedno i prvi član, b_{3*0+1}=b_1 (tu se dobro vidi kako treba dozvoliti i 0 za k ... prvi prirodni n koji daje ostatak 1 pri dijeljenju s 3 je naravno n=1 , a on je 3*(k=0)+1 .
Izračunamo, to je infS1=minS1=b_1=5-1/3=14/3 .
Također, jer taj podniz raste, supremum slike mu je jednak limesu, dakle 5 .
Sad za S2 , dobiven uzevši one preostale n-ove , koji daju ostatak 2 pri dijeljenju s 3 , vjerujem da stvarno možeš (i trebaš) sam. Trebaš dobiti infS2=29/6 & supS2=5 .
I onda naravno, supS=max{supS0,supS1,supS2}=5 , a infS=min{5,14/3,29/6}=14/3 . Oba se postižu, za npr. n=3 i n=1 redom.
I zadnji zadatak...
[quote]sam dobro rijesio?[/quote]
Nisi.
Rastav na slučajeve mod 4 je dobar, ali ima ih *4* , zaBoga... zaboravio si 4k+1 . :-/
Osim toga, treba biti malo pažljiviji pri gledanju koji podnizovi rastu a koji padaju, što utječe na to što je infimum, a što supremum.
I za kraj, kao što već par puta rekoh gore, ako je n=4k+1 i n prirodan broj, onda je k prirodan broj _ili nula_. Jedini slučaj ovog tipa kad nije tako je kad je n djeljiv s 4 , n=4k . Tada naravno, n@|N => k@|N .
Ajd sad riješi zadatak.
HTH,
| Pajo (napisa): | | veky (napisa): |
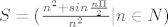
Kao što napisa, imaš sliku niza zadanog s a_n:=1+sin(npi/2)/n^2 . Sad imaš tri slučaja, odnosno S se rastavlja na tri skupa.
U prvom slučaju, n=2k . Tada je sin(npi/2)=sin(kpi)=0 ⇒ a_2k=1 . Supremum i infimum tog podskupa su očito 1 . 
U drugom slučaju, imaš n=4k+1 , k@\N . Tada je sin(npi/2)=sin(2kpi+pi/2)=sin(pi/2)=1 , pa imaš 1+1/(4k+1)^2 . To pada, pa je supremum onaj prvi, 1+1/1=2 , a infimum je limes, dakle 1 .
U trećem slučaju, imaš n=4k+3 , k@\N . Tada je ovaj sinus jednak -1 , pa ti član niza izgleda 1-1/(4k+3)^2 . To raste, pa je supremum jednak limesu, 1 , a infimum je jednak prvom članu, 1-1/3^2=8/9 .
Sve skupa, infS=min{1,1,8/9}=8/9 , a supS=max{1,2,1}=2 . Oba se naravno postižu, jedan za n=3 , drugi za n=1 .
|
Bi se moglo umjesto drugog slučaja n=4k+1 uzeti n=2k+3,a umjesto treceg slucaja n=4k+3 uzeti n=2k+1? |
Ne. Bar dok ne napišeš što je k . Podrazumijeva se (i zato i ideš s takvom supstitucijom, da dobiješ novi _niz_) da k ide po |N (ili \N=|NU{0} ). No u tom slučaju, 2k+1 i 2k+3 kupe više-manje iste brojeve (osim broja 1 ): neparne. Na primjer, 7 je i oblika 2k+1 (za k=3 ) i oblika 2k+3 (za k=2 ).
Drugi razlog je taj što ti takvi slučajevi neće puno pomoći, čak ni da čine particiju... stvar je u tome da i dalje ne znaš što ti je sin(kpi/2) . Ok, ako je k=2k+1 , imaš da je to sin(kpi+pi/2) , no i dalje to može biti i -1 i 1 (konkretno, ovdje je to (-1)^k ).
Point ovog gornjeg rastavljanja na slučajeve je upravo u tome da u svakom tom slučaju dobiješ jednostavnu konstantu za taj sin , da ti se razlomak pojednostavi.
| Citat: | Imamo tri slucaja,3 skupa.
prvi slucaj n=2k+1 |
Gr. Gle gore... ista vrsta greške. Ne rastavljaš s obzirom na ostatke pri dijeljenju s 2 , već s 3  Inače, 2k+1 i 2k+3 bi ti opet bila skoro ista stvar – neparni brojevi; a osim toga, ne bi mogao zaključiti da je (2k+l)/3-floor((2k+l)/3) neka konstantna vrijednost (jer nije).
| Citat: |  |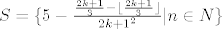
Ovo nema baš puno smisla. Ako karakteristični element skupa ovisi o k , treba izgradnju skupa kvantificirati po k . Na primjer, ako n daje ostatak 2 pri dijeljenju s 3 , i n je prirodan broj, tada je n=3k+2 , gdje je k@\N . Dakle gornji skup (i, povrh svega, to nije S općenito – samo neki njegov podskup, jer smo uzeli samo neke n ) je S2={...| k@\N} .
| Citat: | Tada je
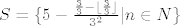
za k=1 pa je supremum i infumum jednak 5. |
Slična stvar. Ne možeš sve podskupove skupa S označavati s S .  Ako si stavio k=1 , imaš samo jedan element od S2 , koji ti onda govori ili ne govori nešto. U ovom konkretnom slučaju, kad bi n bio djeljiv s 3 , cijeli S0 je zapravo jedank {5} , pa to i nije tolika pogreška. No u donjim slučajevima jest.
Nije.
Ok, ajmo ispočetka. Neka je S slika nekog niza, koji označimo s (b_n)_n . Naravno, b_n:=5-(n/3-floor(n/3))/n^2 . Da bismo lakše ispitali ponašanje niza b_n , podijelit ćemo ga u tri podniza: za n=3k , n=3k+1 i n=3k+2 .
Prvi podniz: n je djeljiv s 3 . Tad je naravno n/3 cijeli broj, pa je n/3-floor(n/3)=0 . Odnosno, b_{3k}=5 , za svaki prirodni k . To je konstantan podniz, i njegova slika je samo singleton S0={5} , sa infimumom i supremumom jednakim 5 .
Drugi: n daje ostatak 1 pri dijeljenju s 3 . Dakle n=3k+1 , no iako je n prirodan broj, to znači da k može biti prirodan broj ili 0 (jasno ovo?). Dakle S1={b_{3k+1} | k@\N} . A tipični član od S1 je b_{3k+1} , takav da je "n"/3=(3k+1)/3=k+1/3 . Očito će najveće cijelo od toga biti k , pa je razlika jednaka 1/3 .
Ukupno imamo b_{3k+1}=5-(1/3)/(3k+1)^2 . Ovaj podniz raste ((s porastom k povećava se i (3k+1)^2 , pa se umanjitelj smanjuje, a budući da je umanjenik konstantan ( 5 ), b_{3k+1} se povećava)), pa je njegov infimum ujedno i minimum, ujedno i prvi član, b_{3*0+1}=b_1 (tu se dobro vidi kako treba dozvoliti i 0 za k ... prvi prirodni n koji daje ostatak 1 pri dijeljenju s 3 je naravno n=1 , a on je 3*(k=0)+1 .
Izračunamo, to je infS1=minS1=b_1=5-1/3=14/3 .
Također, jer taj podniz raste, supremum slike mu je jednak limesu, dakle 5 .
Sad za S2 , dobiven uzevši one preostale n-ove , koji daju ostatak 2 pri dijeljenju s 3 , vjerujem da stvarno možeš (i trebaš) sam. Trebaš dobiti infS2=29/6 & supS2=5 .
I onda naravno, supS=max{supS0,supS1,supS2}=5 , a infS=min{5,14/3,29/6}=14/3 . Oba se postižu, za npr. n=3 i n=1 redom.
I zadnji zadatak...
| Citat: | | sam dobro rijesio? |
Nisi.
Rastav na slučajeve mod 4 je dobar, ali ima ih *4* , zaBoga... zaboravio si 4k+1 . :-/
Osim toga, treba biti malo pažljiviji pri gledanju koji podnizovi rastu a koji padaju, što utječe na to što je infimum, a što supremum.
I za kraj, kao što već par puta rekoh gore, ako je n=4k+1 i n prirodan broj, onda je k prirodan broj _ili nula_. Jedini slučaj ovog tipa kad nije tako je kad je n djeljiv s 4 , n=4k . Tada naravno, n@|N ⇒ k@|N .
Ajd sad riješi zadatak.
HTH,
|
