| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pefri
Forumaš(ica)

Pridružen/a: 09. 02. 2005. (22:34:29)
Postovi: (20)16
|
 Postano: 0:17 pon, 14. 2. 2005 Naslov: FUI Postano: 0:17 pon, 14. 2. 2005 Naslov: FUI |
    |
|
|
Evo malo zadataka i iz fui koje ne znam ili mi treba kontrola dal dobro radim:
1. Koliko se šestero znamenkastih brojeva može napraviti od znamenaka broja 3457359497 tako da dvije jednake znamenke ne budu jedna pored druge.
2.Koliko ima permutacija od N_7 koje imaju fiksnu točku među parnim brojevima?
3.Na koliko načina možemo n različitih predmeta razmjestiti u r različitih kutija tako da točno 3 kutije ostanu prazne? A barem 3 prazne?
4. Koliko ima permutacija skupa {a,a,b,b,c,c} u kojima niti jedno slovo se ne pojavljuje na istom mjestu kao u permutaciji bbccaa?
5. Od 200 studenata 100 ih je polozilo MA3, 150 K, 175 RP1, 75 MA3 i K, 80 MA3 i RP1, 130 K i RP1.
a) dokažite da najviše 5 studenata nije položilo niti jedan ispit.
b)koliko najviše, a koliko najmanje studenata je položilo sva 3 ispita?
(treba mi samo uputa kako zapoceti rjesavati jer kontradikcijom da ih ima 6 nista ne dobijem!!!)
Moje rješenje prvog zadatka:
Znači radi se o multiskupu. Ukupan broj permutacija je (5//3)6!/2!2!2! + (5//2)*(5//3)*6!/1!1!2!2! + (5//1)* 6!/2!1!1!1!1!= 8100
S A_1 označimo skup svih 6-perm. s jednim parom od dvije jednake cifre npr 33 jedna kraj druge i |A_1|= (4//2)* 6!/2!2!2! + 6!/2!1!1!1!1!
Tako za |A_1 presjek A_2|, itd.
Rješenje se dobije:
|A_1^c presjek ... presjek A_5^c|=8100-5*|A_1| + (5//2)|A_1 presjek A_2|-...- (5//5)|A_1 presjek ... presjek A_5|
Da li je ovo dobar način?
Moje rješenje drugog zadatka:
Rješenje mi dođe: 7!-3*6!*D_6 + 3*5!*D_5 - D_4
Moje rješenje trećeg zadatka:
T.d.su točno 3 prazne dobijem (4 povrh 3)*1
Da barem 3 budu prazne:
Ukupno slučajeva: r^n
Niti jedna nije prazna: r!*{n//r}
A_i skup svih razmjestaja (preslikavanja) tako da je i-ta kutija prazna |A_i|=(r-1)^n
|A_i presjek A_j|= (r-2)^n
Pa bi rješenje bilo r^n - r!*{n//r} - (r-1)^n - (r-2)^n (ovo nije dobro jer smo u ovom slučaju previše toga po mom misljenju oduzeli -MOje pitanje je kako izbjeći te slučajeve?)
4.zadatak - Ovdje se radi o dearanžmanima al ne znam kako započeti ovaj zadatak pa trebam pomoć!!
Evo malo zadataka i iz fui koje ne znam ili mi treba kontrola dal dobro radim:
1. Koliko se šestero znamenkastih brojeva može napraviti od znamenaka broja 3457359497 tako da dvije jednake znamenke ne budu jedna pored druge.
2.Koliko ima permutacija od N_7 koje imaju fiksnu točku među parnim brojevima?
3.Na koliko načina možemo n različitih predmeta razmjestiti u r različitih kutija tako da točno 3 kutije ostanu prazne? A barem 3 prazne?
4. Koliko ima permutacija skupa {a,a,b,b,c,c} u kojima niti jedno slovo se ne pojavljuje na istom mjestu kao u permutaciji bbccaa?
5. Od 200 studenata 100 ih je polozilo MA3, 150 K, 175 RP1, 75 MA3 i K, 80 MA3 i RP1, 130 K i RP1.
a) dokažite da najviše 5 studenata nije položilo niti jedan ispit.
b)koliko najviše, a koliko najmanje studenata je položilo sva 3 ispita?
(treba mi samo uputa kako zapoceti rjesavati jer kontradikcijom da ih ima 6 nista ne dobijem!!!)
Moje rješenje prvog zadatka:
Znači radi se o multiskupu. Ukupan broj permutacija je (5//3)6!/2!2!2! + (5//2)*(5//3)*6!/1!1!2!2! + (5//1)* 6!/2!1!1!1!1!= 8100
S A_1 označimo skup svih 6-perm. s jednim parom od dvije jednake cifre npr 33 jedna kraj druge i |A_1|= (4//2)* 6!/2!2!2! + 6!/2!1!1!1!1!
Tako za |A_1 presjek A_2|, itd.
Rješenje se dobije:
|A_1^c presjek ... presjek A_5^c|=8100-5*|A_1| + (5//2)|A_1 presjek A_2|-...- (5//5)|A_1 presjek ... presjek A_5|
Da li je ovo dobar način?
Moje rješenje drugog zadatka:
Rješenje mi dođe: 7!-3*6!*D_6 + 3*5!*D_5 - D_4
Moje rješenje trećeg zadatka:
T.d.su točno 3 prazne dobijem (4 povrh 3)*1
Da barem 3 budu prazne:
Ukupno slučajeva: r^n
Niti jedna nije prazna: r!*{n//r}
A_i skup svih razmjestaja (preslikavanja) tako da je i-ta kutija prazna |A_i|=(r-1)^n
|A_i presjek A_j|= (r-2)^n
Pa bi rješenje bilo r^n - r!*{n//r} - (r-1)^n - (r-2)^n (ovo nije dobro jer smo u ovom slučaju previše toga po mom misljenju oduzeli -MOje pitanje je kako izbjeći te slučajeve?)
4.zadatak - Ovdje se radi o dearanžmanima al ne znam kako započeti ovaj zadatak pa trebam pomoć!!
|
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
 Postano: 3:52 pon, 14. 2. 2005 Naslov: Postano: 3:52 pon, 14. 2. 2005 Naslov: |
    |
|
|
[quote]4. Koliko ima permutacija skupa {a,a,b,b,c,c} u kojima niti jedno slovo se ne pojavljuje na istom mjestu kao u permutaciji bbccaa?[/quote]
zadnji ti mogu zdravoseljacki, ne znam koristi li ti to, ali... nek se nadje
neka su nam to "slotovi" 1..6
na prva dva ne smije doci slovo b.
ako stavimo dva slova "a", onda nuzno mora biti aabbcc
analogno, ako stavimo dva slova c, mora biti ccaabb
preostaje nam slucaj kada su prva dva znaka "ac" (ili "ca", ali to cemo kasnije).
tada je nuzno nasa permutacija oblika "ac" "ab" "bc".
jos svaki par mozemo permutirati na dva nacina, pa to skupa cini 8 nacina (2*2*2).
sve zajedno, to je bijednih 10 :).
| Citat: | | 4. Koliko ima permutacija skupa {a,a,b,b,c,c} u kojima niti jedno slovo se ne pojavljuje na istom mjestu kao u permutaciji bbccaa? |
zadnji ti mogu zdravoseljacki, ne znam koristi li ti to, ali... nek se nadje
neka su nam to "slotovi" 1..6
na prva dva ne smije doci slovo b.
ako stavimo dva slova "a", onda nuzno mora biti aabbcc
analogno, ako stavimo dva slova c, mora biti ccaabb
preostaje nam slucaj kada su prva dva znaka "ac" (ili "ca", ali to cemo kasnije).
tada je nuzno nasa permutacija oblika "ac" "ab" "bc".
jos svaki par mozemo permutirati na dva nacina, pa to skupa cini 8 nacina (2*2*2).
sve zajedno, to je bijednih 10 :).
_________________  |
|
| [Vrh] |
|
pefri
Forumaš(ica)

Pridružen/a: 09. 02. 2005. (22:34:29)
Postovi: (20)16
|
 Postano: 10:09 pon, 14. 2. 2005 Naslov: Postano: 10:09 pon, 14. 2. 2005 Naslov: |
    |
|
|
[quote="ahri"][quote]4. Koliko ima permutacija skupa {a,a,b,b,c,c} u kojima niti jedno slovo se ne pojavljuje na istom mjestu kao u permutaciji bbccaa?[/quote]
zadnji ti mogu zdravoseljacki, ne znam koristi li ti to, ali... nek se nadje
neka su nam to "slotovi" 1..6
na prva dva ne smije doci slovo b.
ako stavimo dva slova "a", onda nuzno mora biti aabbcc
analogno, ako stavimo dva slova c, mora biti ccaabb
preostaje nam slucaj kada su prva dva znaka "ac" (ili "ca", ali to cemo kasnije).
tada je nuzno nasa permutacija oblika "ac" "ab" "bc".
jos svaki par mozemo permutirati na dva nacina, pa to skupa cini 8 nacina (2*2*2).
sve zajedno, to je bijednih 10 :).[/quote]
da, to je to! Hvala! To sam htjela nekako riješiti s formulom za dearanžmane al tako mi nije islo!
| ahri (napisa): | | Citat: | | 4. Koliko ima permutacija skupa {a,a,b,b,c,c} u kojima niti jedno slovo se ne pojavljuje na istom mjestu kao u permutaciji bbccaa? |
zadnji ti mogu zdravoseljacki, ne znam koristi li ti to, ali... nek se nadje
neka su nam to "slotovi" 1..6
na prva dva ne smije doci slovo b.
ako stavimo dva slova "a", onda nuzno mora biti aabbcc
analogno, ako stavimo dva slova c, mora biti ccaabb
preostaje nam slucaj kada su prva dva znaka "ac" (ili "ca", ali to cemo kasnije).
tada je nuzno nasa permutacija oblika "ac" "ab" "bc".
jos svaki par mozemo permutirati na dva nacina, pa to skupa cini 8 nacina (2*2*2).
sve zajedno, to je bijednih 10  . . |
da, to je to! Hvala! To sam htjela nekako riješiti s formulom za dearanžmane al tako mi nije islo!
|
|
| [Vrh] |
|
Ashley
Forumaš(ica)


Pridružen/a: 30. 04. 2004. (22:54:03)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Ashley
Forumaš(ica)


Pridružen/a: 30. 04. 2004. (22:54:03)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
pefri
Forumaš(ica)

Pridružen/a: 09. 02. 2005. (22:34:29)
Postovi: (20)16
|
 Postano: 22:41 uto, 15. 2. 2005 Naslov: odgovor Postano: 22:41 uto, 15. 2. 2005 Naslov: odgovor |
    |
|
|
[quote="Anonymous"]neka je S=(1,2,3,.......2003)
A)odredite broj troclanih podskupova od s kojima je zbroj elemenata djeljiv sa 3?
b) kojima je djeljiv sa 4?
jel mi moze molim vas neko ovo probati rjesiti.unaprijed hvala[/quote]
Tročlane sume idu od 6,7, ..., 6006. Brojeva manjih od 6006 djeljivih s 3 ima: 6006/3=2002 - 1 (to je trojka jer gledamo brojeve pocevsi od 6)=2001
isto tako za b)
| Anonymous (napisa): | neka je S=(1,2,3,.......2003)
A)odredite broj troclanih podskupova od s kojima je zbroj elemenata djeljiv sa 3?
b) kojima je djeljiv sa 4?
jel mi moze molim vas neko ovo probati rjesiti.unaprijed hvala |
Tročlane sume idu od 6,7, ..., 6006. Brojeva manjih od 6006 djeljivih s 3 ima: 6006/3=2002 - 1 (to je trojka jer gledamo brojeve pocevsi od 6)=2001
isto tako za b)
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 22:58 uto, 15. 2. 2005 Naslov: Re: odgovor Postano: 22:58 uto, 15. 2. 2005 Naslov: Re: odgovor |
    |
|
|
[quote="pefri"][quote="Anonymous"]neka je S=(1,2,3,.......2003)
A)odredite broj troclanih podskupova od s kojima je zbroj elemenata djeljiv sa 3?
b) kojima je djeljiv sa 4?
jel mi moze molim vas neko ovo probati rjesiti.unaprijed hvala[/quote]
Tročlane sume idu od 6,7, ..., 6006. Brojeva manjih od 6006 djeljivih s 3 ima: 6006/3=2002 - 1 (to je trojka jer gledamo brojeve pocevsi od 6)=2001
isto tako za b)[/quote]
Malo vise nisam "doma" s kombinatorikom, :oops: ali cini mi se da se neke od tih suma mogu dobiti na vise nacina nego neke druge, sto mi se bas i ne cini zanemarivo... :?
| pefri (napisa): | | Anonymous (napisa): | neka je S=(1,2,3,.......2003)
A)odredite broj troclanih podskupova od s kojima je zbroj elemenata djeljiv sa 3?
b) kojima je djeljiv sa 4?
jel mi moze molim vas neko ovo probati rjesiti.unaprijed hvala |
Tročlane sume idu od 6,7, ..., 6006. Brojeva manjih od 6006 djeljivih s 3 ima: 6006/3=2002 - 1 (to je trojka jer gledamo brojeve pocevsi od 6)=2001
isto tako za b) |
Malo vise nisam "doma" s kombinatorikom,  ali cini mi se da se neke od tih suma mogu dobiti na vise nacina nego neke druge, sto mi se bas i ne cini zanemarivo... ali cini mi se da se neke od tih suma mogu dobiti na vise nacina nego neke druge, sto mi se bas i ne cini zanemarivo... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
ahri
Forumaš(ica)


Pridružen/a: 19. 11. 2003. (23:16:07)
Postovi: (193)16
|
 Postano: 1:08 sri, 16. 2. 2005 Naslov: Postano: 1:08 sri, 16. 2. 2005 Naslov: |
    |
|
|
tako je, neke sume mozes dobiti na vise nacina... to cu ja sad, samo da ne zaspim :))) [vjerojatno ide edit ovog posta]
ali... svaki od tih brojeva mozes zapisati kao 3k, 3k+1, 3k+2
i da bi bila suma djeljiva s 3 imas sljedece kombinacije brojeva (opcih)
3a, 3b, 3c
3a+1, 3b+1, 3c+1
3a+2, 3b+2, 3c+2
3a, 3b+1, 3c+2
i sad... izracunas koliko kojih kombinacija ima, one su _disjunktne_ i to zbojis.
a) 3a, 3b, 3c
u ovom skupu brojeva koji su dijeljivi s 3 ima 667.
dakle, ovih kombinacija ima [latex]667\choose3 [/latex]
b) 3a+1, 3b+1, 3c+1
ovih ima 668, dakle, [latex]668\choose3 [/latex]
c) 3a+2, 3b+2, 3c+2
i ovih ima 668, dakle, [latex]668\choose3 [/latex]
d) 3a, 3b+1, 3c+2
e sad... tu biras jednu od 667, jednu od 668, i jednu od 668.
dakle, 667*668*668.
[latex]{667 \choose 3} + {668 \choose 3} +{668 \choose3}+ 667 \times 668 \times 668[/latex]
tako je, neke sume mozes dobiti na vise nacina... to cu ja sad, samo da ne zaspim :))) [vjerojatno ide edit ovog posta]
ali... svaki od tih brojeva mozes zapisati kao 3k, 3k+1, 3k+2
i da bi bila suma djeljiva s 3 imas sljedece kombinacije brojeva (opcih)
3a, 3b, 3c
3a+1, 3b+1, 3c+1
3a+2, 3b+2, 3c+2
3a, 3b+1, 3c+2
i sad... izracunas koliko kojih kombinacija ima, one su _disjunktne_ i to zbojis.
a) 3a, 3b, 3c
u ovom skupu brojeva koji su dijeljivi s 3 ima 667.
dakle, ovih kombinacija ima 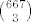
b) 3a+1, 3b+1, 3c+1
ovih ima 668, dakle, 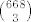
c) 3a+2, 3b+2, 3c+2
i ovih ima 668, dakle, 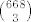
d) 3a, 3b+1, 3c+2
e sad... tu biras jednu od 667, jednu od 668, i jednu od 668.
dakle, 667*668*668.
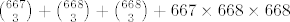
_________________  |
|
| [Vrh] |
|
|







