|
Ah, pa to i nije prava zadaca. To sam bio zadao kao primjer dva jako teska zadatka uz napomenu da niposto [b]nisu za pismeni[/b] i da ih probaju rijesiti samo oni ambiciozniji.
[quote="Void"]1. V KDVP nad poljem K. Ako je [latex]A \in L(V), A \neq \lambda I, \forall \lambda \in K[/latex], onda postoji baza od V u kojoj matrica od A na dijagonali ima [latex]\underbrace{0, \ldots, 0}_{dimV-1}, tr(A)[/latex][/quote]
Ovo je zadatak iz zbirke
http://www.math.su.se/~mleites/Prasolov/prasLinAlg/
a drugo rjesenje se moze naci ovdje
http://www.ucl.ac.uk/~ucahjej/imc/imc2001/prob_sol1.pdf
ali ta rjesenja mi se cine ruzna i spetljana.
Ja sam zamislio da se to rijesi (slicno kao i u spomenutom zadatku s vjezbi) indukcijom po dimenziji. Korak indukcije je gotovo isti kao i u zadatku s vjezbi: nadje se baza u kojoj matrica ima 0 u gornjem lijevom uglu. Ipak, nije sasvim trivijalno raspisati sve tehnicke detalje (npr. zasto inducirani operator na (n-1)-dim potprostoru nije skalarni visekratnik od I, tako da onda doista mozemo iskoristiti pretpostavku indukcije.)
[quote="Void"]2. V kompleksni KDVP. Ako je [latex]A \in L(V), A \neq 0[/latex], onda postoji baza od V u kojoj matrica od A na dijagonali nema niti jednu nulu.[/quote]
Ovo je isto zadatak iz zbirke
http://www.math.su.se/~mleites/Prasolov/prasLinAlg/
Ideja rjesenja je negdje na liniji spomenutih zadataka.
Ovaj zadatak se zapravo cak moze svesti na prethodni. Naime, ako A nije skalarni visekratnik od I (inace je trivijalno), onda iskoristimo prethodni zadatak za operator A-aI (za neki pogodno odabrani skalar a). Tada ce matrica od A u toj bazi na dijagonali imati
a,...,a,tr(A)-(n-1)a,
sto nece biti nule ako izaberemo a!=0, a!=tr(A)/(n-1).
Ah, pa to i nije prava zadaca. To sam bio zadao kao primjer dva jako teska zadatka uz napomenu da niposto nisu za pismeni i da ih probaju rijesiti samo oni ambiciozniji.
| Void (napisa): | 1. V KDVP nad poljem K. Ako je 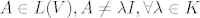 , onda postoji baza od V u kojoj matrica od A na dijagonali ima  |
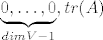Ovo je zadatak iz zbirke
http://www.math.su.se/~mleites/Prasolov/prasLinAlg/
a drugo rjesenje se moze naci ovdje
http://www.ucl.ac.uk/~ucahjej/imc/imc2001/prob_sol1.pdf
ali ta rjesenja mi se cine ruzna i spetljana.
Ja sam zamislio da se to rijesi (slicno kao i u spomenutom zadatku s vjezbi) indukcijom po dimenziji. Korak indukcije je gotovo isti kao i u zadatku s vjezbi: nadje se baza u kojoj matrica ima 0 u gornjem lijevom uglu. Ipak, nije sasvim trivijalno raspisati sve tehnicke detalje (npr. zasto inducirani operator na (n-1)-dim potprostoru nije skalarni visekratnik od I, tako da onda doista mozemo iskoristiti pretpostavku indukcije.)
| Void (napisa): | 2. V kompleksni KDVP. Ako je 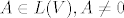 , onda postoji baza od V u kojoj matrica od A na dijagonali nema niti jednu nulu. |
Ovo je isto zadatak iz zbirke
http://www.math.su.se/~mleites/Prasolov/prasLinAlg/
Ideja rjesenja je negdje na liniji spomenutih zadataka.
Ovaj zadatak se zapravo cak moze svesti na prethodni. Naime, ako A nije skalarni visekratnik od I (inace je trivijalno), onda iskoristimo prethodni zadatak za operator A-aI (za neki pogodno odabrani skalar a). Tada ce matrica od A u toj bazi na dijagonali imati
a,...,a,tr(A)-(n-1)a,
sto nece biti nule ako izaberemo a!=0, a!=tr(A)/(n-1).
Zadnja promjena: vjekovac; 19:47 sub, 16. 4. 2005; ukupno mijenjano 1 put.
|
