| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 15:34 ned, 17. 4. 2005 Naslov: 3. zadatak - rok 8.2.2005 Postano: 15:34 ned, 17. 4. 2005 Naslov: 3. zadatak - rok 8.2.2005 |
    |
|
|
Dopunite do ortogonalne (s obzirom na skalarni produkt) baze za [latex]R^4[/latex] skup
[latex]{(1,-2,2,-3),(2,-3,2,4)}[/latex]
dakle...ovo je moja logika rjesavanja...ispravite ako sam u krivu.
dakle...definirat cemo skup [latex]M={(1,-2,2,-3),(2,-3,2,4)}={a,b}, dim M=2[/latex]
ortogonalna baza sadrzava 2 vektora jer je [latex]dim M=2[/latex], pa je i [latex]dim M^\bot=2, M \oplus M^\bot=R^4[/latex].
definirat cemo vektor [latex]x \in M^\bot \Leftrightarrow <x|a>=0, <x|b>=0, x=(x_1,x_2,x_3,x_4)[/latex]
dakle...dobije se sljedece:
[latex]<x|a>=x_1-2x_2,+2x_3-3x_4=0[/latex]
[latex]<x|b>=2x_1-3x_2+2x_3+4x_4=0[/latex]
kad se to malo sredi...dobio sam sljedece jednadzbe:
[latex]x_1=-3x_3-17x_4[/latex]
[latex]x_2=x_1+7x_4 \Rightarrow x_2=-3x_3-10x_4[/latex]
dakle...vektori koji se traze su:
[latex]M^\bot={(-3,-3,1,0),(-17,-10,0,1)}[/latex]
da li je logika dobra i da li sam dobrim postupkom rjesavao zadatak?
Dopunite do ortogonalne (s obzirom na skalarni produkt) baze za 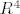 skup skup
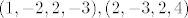
dakle...ovo je moja logika rjesavanja...ispravite ako sam u krivu.
dakle...definirat cemo skup 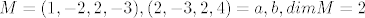
ortogonalna baza sadrzava 2 vektora jer je 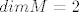 , pa je i , pa je i 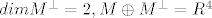 . .
definirat cemo vektor 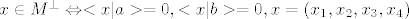
dakle...dobije se sljedece:
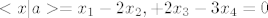
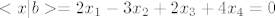
kad se to malo sredi...dobio sam sljedece jednadzbe:
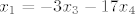
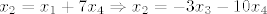
dakle...vektori koji se traze su:
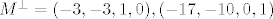
da li je logika dobra i da li sam dobrim postupkom rjesavao zadatak?
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)


Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)


Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)


Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
|
| [Vrh] |
|
Tonci
Forumaš(ica)


Pridružen/a: 31. 10. 2002. (13:46:40)
Postovi: (61)16
Spol: 
Lokacija: Split
|
 Postano: 14:35 pon, 18. 4. 2005 Naslov: Re: 3. zadatak - rok 8.2.2005 Postano: 14:35 pon, 18. 4. 2005 Naslov: Re: 3. zadatak - rok 8.2.2005 |
    |
|
|
[quote="HijenA"]
kad se to malo sredi...dobio sam sljedece jednadzbe:
[latex]x_1=-3x_3-17x_4[/latex]
[latex]x_2=x_1+7x_4 \Rightarrow x_2=-3x_3-10x_4[/latex]
[/quote]
Ja dobijem jednadzbe
x1 = 2*x_3 - 17*x_4
x2 = 2*x_3 - 10*x_4
(ali racunao sam na brzinu pa ti jos provjeri)
to je bio uvjet da je neki vektor (x_1,x_2,x_3,x_4) okomit na dva dana vektora. Pa izaberimo jedan takav vektor, npr. (2,2,1,0).
Sada cetvrti vektor mora biti okomit i na toga, sto nam daje i cetvrtu jednadzbu:
2*x_1 + 2*x_2 + x_3 = 0.
Zajedno s one dvije jednadzbe gore, to mi daje:
x_3 = 6*x_4.
Uzmem x_4 = 1 i dobijem vektor (-5,2,6,1).
| HijenA (napisa): |
kad se to malo sredi...dobio sam sljedece jednadzbe:
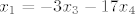
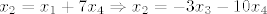
|
Ja dobijem jednadzbe
x1 = 2*x_3 - 17*x_4
x2 = 2*x_3 - 10*x_4
(ali racunao sam na brzinu pa ti jos provjeri)
to je bio uvjet da je neki vektor (x_1,x_2,x_3,x_4) okomit na dva dana vektora. Pa izaberimo jedan takav vektor, npr. (2,2,1,0).
Sada cetvrti vektor mora biti okomit i na toga, sto nam daje i cetvrtu jednadzbu:
2*x_1 + 2*x_2 + x_3 = 0.
Zajedno s one dvije jednadzbe gore, to mi daje:
x_3 = 6*x_4.
Uzmem x_4 = 1 i dobijem vektor (-5,2,6,1).
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 16:39 pon, 18. 4. 2005 Naslov: Re: 3. zadatak - rok 8.2.2005 Postano: 16:39 pon, 18. 4. 2005 Naslov: Re: 3. zadatak - rok 8.2.2005 |
    |
|
|
[quote="Tonci"][quote="HijenA"]
kad se to malo sredi...dobio sam sljedece jednadzbe:
[latex]x_1=-3x_3-17x_4[/latex]
[latex]x_2=x_1+7x_4 \Rightarrow x_2=-3x_3-10x_4[/latex]
[/quote]
Ja dobijem jednadzbe
x1 = 2*x_3 - 17*x_4
x2 = 2*x_3 - 10*x_4
(ali racunao sam na brzinu pa ti jos provjeri)
to je bio uvjet da je neki vektor (x_1,x_2,x_3,x_4) okomit na dva dana vektora.[/quote]
nije li to dovoljno? i onda izlucimo [latex]x_3, x_4[/latex] te dobijemo
[latex]x_3(2,2,1,0)+x_4(-17,-10,0,1)[/latex] i ta dva vektora, zajedno sa pocetnima, cine bazu prostora [latex]R^4[/latex]
[quote]
Pa izaberimo jedan takav vektor, npr. (2,2,1,0).
Sada cetvrti vektor mora biti okomit i na toga, sto nam daje i cetvrtu jednadzbu:
2*x_1 + 2*x_2 + x_3 = 0.
Zajedno s one dvije jednadzbe gore, to mi daje:
x_3 = 6*x_4.
Uzmem x_4 = 1 i dobijem vektor (-5,2,6,1).[/quote]
ne kuzim...sto si htio ovime reci?
| Tonci (napisa): | | HijenA (napisa): |
kad se to malo sredi...dobio sam sljedece jednadzbe:
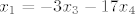
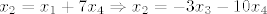
|
Ja dobijem jednadzbe
x1 = 2*x_3 - 17*x_4
x2 = 2*x_3 - 10*x_4
(ali racunao sam na brzinu pa ti jos provjeri)
to je bio uvjet da je neki vektor (x_1,x_2,x_3,x_4) okomit na dva dana vektora. |
nije li to dovoljno? i onda izlucimo 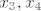 te dobijemo te dobijemo
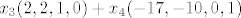 i ta dva vektora, zajedno sa pocetnima, cine bazu prostora i ta dva vektora, zajedno sa pocetnima, cine bazu prostora 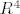
| Citat: |
Pa izaberimo jedan takav vektor, npr. (2,2,1,0).
Sada cetvrti vektor mora biti okomit i na toga, sto nam daje i cetvrtu jednadzbu:
2*x_1 + 2*x_2 + x_3 = 0.
Zajedno s one dvije jednadzbe gore, to mi daje:
x_3 = 6*x_4.
Uzmem x_4 = 1 i dobijem vektor (-5,2,6,1). |
ne kuzim...sto si htio ovime reci?
|
|
| [Vrh] |
|
|













