| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Studos
Gost
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
creativeri
Forumaš(ica)

Pridružen/a: 02. 05. 2005. (18:51:10)
Postovi: (8)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 20:25 pon, 9. 5. 2005 Naslov: Re: Nekoliko laganih zadataka Postano: 20:25 pon, 9. 5. 2005 Naslov: Re: Nekoliko laganih zadataka |
    |
|
|
[quote="Studos"]1. Iz točke O polazi 2ˆn osoba u smjeru osi x i 2ˆ(n-1) osoba u smjeru osi y. Na svakom slijedećem raskrižju (u svakoj točki s cjelobrojnim koordinatama) svaka grupa se ponovno dijeli na isti način. Poznato je da je u točku A(p,q) stiglo t osoba. Koliko je osoba krenulo iz točke O?[/quote]
Meni ovo nije jasno... :zbunj:
U tocki O se njih [latex]3*2^{n-1}[/latex] podijelilo u omjeru 2:1, tj. u grupe od [latex]2*2^{n-1}[/latex] i [latex]1*2^{n-1}[/latex] (dakle 2/3 grupe ode po osi x i 1/3 grupe po osi y). :)
Kako se onda na sljedecem raskrizju grupe od [latex]2^{nesto}[/latex] mogu dijeliti na isti nacin, dakle na trecine? :grebgreb:
| Studos (napisa): | | 1. Iz točke O polazi 2ˆn osoba u smjeru osi x i 2ˆ(n-1) osoba u smjeru osi y. Na svakom slijedećem raskrižju (u svakoj točki s cjelobrojnim koordinatama) svaka grupa se ponovno dijeli na isti način. Poznato je da je u točku A(p,q) stiglo t osoba. Koliko je osoba krenulo iz točke O? |
Meni ovo nije jasno... 
U tocki O se njih 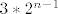 podijelilo u omjeru 2:1, tj. u grupe od podijelilo u omjeru 2:1, tj. u grupe od 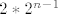 i i 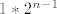 (dakle 2/3 grupe ode po osi x i 1/3 grupe po osi y). (dakle 2/3 grupe ode po osi x i 1/3 grupe po osi y). 
Kako se onda na sljedecem raskrizju grupe od 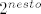 mogu dijeliti na isti nacin, dakle na trecine? mogu dijeliti na isti nacin, dakle na trecine? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
|





