Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

integral
WWW:

Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
gic
Gost
PostPostano: 10:03 sri, 1. 9. 2004    Naslov: integral Citirajte i odgovorite
zasto integral łdx/cos^2xtgx = łdx/cos^2xsinx/cosx nije = ł dx/1/2sin2x
zasto integral łdx/cos^2xtgx = łdx/cos^2xsinx/cosx nije = ł dx/1/2sin2x


[Vrh]
Crni
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: muško
Sarma = la pohva - posuda
4 = 29 - 25
Lokacija: Zagreb
PostPostano: 10:33 sri, 1. 9. 2004    Naslov: Citirajte i odgovorite
Nisam siguran na kaj misliš. Možda ovo:

[latex]\int cos^{2}x\cdot tgxdx=\int cosx\cdot sinxdx=\frac{1}{2}\int sin2xdx=/t=2x, dx=\frac{dt}{2}/=\frac{1}{4}\int sintdt=-\frac{1}{4}cost+C=-\frac{1}{4}cos2x+C[/latex]?
Nisam siguran na kaj misliš. Možda ovo:

?




Zadnja promjena: Crni; 11:33 čet, 2. 9. 2004; ukupno mijenjano 1 put.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Gost
PostPostano: 8:26 čet, 2. 9. 2004    Naslov: Citirajte i odgovorite
moze i tako ali sam mislio kad je taj tvoj integral u razlomku. Naime kad sam ja to napravio ko i ti (skratio ) rezultat mi nije ispao tocan
moze i tako ali sam mislio kad je taj tvoj integral u razlomku. Naime kad sam ja to napravio ko i ti (skratio ) rezultat mi nije ispao tocan


[Vrh]
veky
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Sarma = la pohva - posuda
22 = 24 - 2
Lokacija: negdje daleko...
PostPostano: 14:12 čet, 2. 9. 2004    Naslov: Citirajte i odgovorite
[quote="Anonymous"]moze i tako ali sam mislio kad je taj tvoj integral u razlomku. Naime kad sam ja to napravio ko i ti (skratio ) rezultat mi nije ispao tocan[/quote]

Transformacija je uvijek ok (osim gdje je nazivnik nula, ali to je uglavnom zanemarivo: ). Druga je stvar što int(1/f) općenito [b]nije[/b] jednako 1/int(f) ... ako je to bio tvoj problem.
Anonymous (napisa):
moze i tako ali sam mislio kad je taj tvoj integral u razlomku. Naime kad sam ja to napravio ko i ti (skratio ) rezultat mi nije ispao tocan


Transformacija je uvijek ok (osim gdje je nazivnik nula, ali to je uglavnom zanemarivo: ). Druga je stvar što int(1/f) općenito nije jednako 1/int(f) ... ako je to bio tvoj problem.


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
filipnet
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: muško
Sarma = la pohva - posuda
24 = 29 - 5
Lokacija: cvrsto na stolici
PostPostano: 18:12 čet, 2. 9. 2004    Naslov: Citirajte i odgovorite
trebam pomoc malu kod dva integrala:
1. dx/[2x+(3x+1)^1/2] integral ide od 0-5, neznam kak da se rijesim ovog korijena, probao sam svakakve suostitucije, nis mi nije uspjelo!
2.dx/(1+e^x+e^2x)^1/2
pomoc? ovaj me e^x ubija u pojam!
trebam pomoc malu kod dva integrala:
1. dx/[2x+(3x+1)^1/2] integral ide od 0-5, neznam kak da se rijesim ovog korijena, probao sam svakakve suostitucije, nis mi nije uspjelo!
2.dx/(1+e^x+e^2x)^1/2
pomoc? ovaj me e^x ubija u pojam!



_________________
Dwarf Everything happens with a reason! Vidi me kako skaaaaaceeeem!
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Crni
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: muško
Sarma = la pohva - posuda
4 = 29 - 25
Lokacija: Zagreb
PostPostano: 23:57 čet, 2. 9. 2004    Naslov: Citirajte i odgovorite
[quote="filipnet"]trebam pomoc malu kod dva integrala:
1. dx/[2x+(3x+1)^1/2] integral ide od 0-5, neznam kak da se rijesim ovog korijena, probao sam svakakve suostitucije, nis mi nije uspjelo!
2.dx/(1+e^x+e^2x)^1/2
pomoc? ovaj me e^x ubija u pojam! [/quote]
[b]1. integral[/b]

[latex]\int(2x+ \sqrt{3x+1})dx=x^{2}+ \int \sqrt{3x+1}dx= / t= \sqrt{3x+1},dx=\frac{2}{3}tdt/=x^{2}+\frac{2}{3} \int t^{2}dt=x^{2}+ \frac{2}{9}t^{3}=x^{2}+ \frac{2}{9}(3x+1)^{\frac{3}{2}}[/latex]


[b]2. integral[/b]

[latex]\int\sqrt{1+e^{x}+e^{2x}}dx=\int\sqrt{\frac{3}{4}+(\frac{1}{2}+e^{x})^{2}}dx=/t=e^{x}/=\int\frac{\sqrt{\frac{3}{4}+(\frac{1}{2}+t)^{2}}}{t}dt=/p=\frac{1}{t}/=\int\frac{\sqrt{p^{2}+p+1}}{p^{2}}dp=/p=tgq/=\int\frac{\sqrt{tg^{2}q+1}}{tg^{2}q}dq=\int\frac{dq}{cosq}+\int\frac{cosq}{sin^{2}q}dq=ln|tgq+\sqrt{1+tg^{2}q}|-\frac{\sqrt{1+tg^2q}}{tgq}+C=ln|p+\sqrt{p^{2}+1}|-\frac{\sqrt{p^{2}+1}}{p}+C=ln|\frac{1+\sqrt{t^{2}+1}}{t}|-\sqrt{t^{2}+1}+C=ln|\frac{1+\sqrt{e^{2x}+1}}{e^{x}}|-\sqrt{e^{2x}+1}+C[/latex]

Daj rista, to malo više vježbaj. Pa onaj prvi je totalno banalan. :)
filipnet (napisa):
trebam pomoc malu kod dva integrala:
1. dx/[2x+(3x+1)^1/2] integral ide od 0-5, neznam kak da se rijesim ovog korijena, probao sam svakakve suostitucije, nis mi nije uspjelo!
2.dx/(1+e^x+e^2x)^1/2
pomoc? ovaj me e^x ubija u pojam!

1. integral




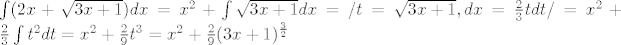
2. integral



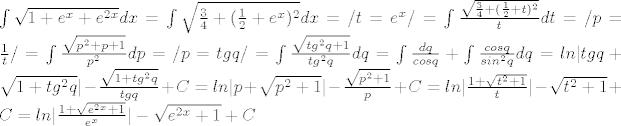
Daj rista, to malo više vježbaj. Pa onaj prvi je totalno banalan. Smile


[Vrh]
Korisnički profil Pošaljite privatnu poruku
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 0:31 pet, 3. 9. 2004    Naslov: Citirajte i odgovorite
[quote="Crni"]Daj rista, to malo više vježbaj. Pa onaj prvi je totalno banalan. :)[/quote]

Daj rista, to malo bolje citaj. :roll: Covjek je pitao ovo:

[latex]\int{dx \over 2x+ \sqrt{3x+1}}[/latex]

[latex]\int{dx \over \sqrt{1+e^{x}+e^{2x}}}[/latex]
Crni (napisa):
Daj rista, to malo više vježbaj. Pa onaj prvi je totalno banalan. Smile


Daj rista, to malo bolje citaj. Rolling Eyes Covjek je pitao ovo:






_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
filipnet
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: muško
Sarma = la pohva - posuda
24 = 29 - 5
Lokacija: cvrsto na stolici
PostPostano: 0:33 pet, 3. 9. 2004    Naslov: Citirajte i odgovorite
Rista, prvi je razlomak, znaci dx kroz sve! kao i drugi!
Rista, prvi je razlomak, znaci dx kroz sve! kao i drugi!



_________________
Dwarf Everything happens with a reason! Vidi me kako skaaaaaceeeem!
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Crni
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: muško
Sarma = la pohva - posuda
4 = 29 - 25
Lokacija: Zagreb
PostPostano: 12:29 pet, 3. 9. 2004    Naslov: Citirajte i odgovorite
OK, sori! I Crni se nekad zariba! :oops:

[latex]\int\frac{dx}{2x+\sqrt{3x+1}}=/t=\sqrt{3x+1}/=\int\frac{2t}{2t^{2}+3t-2}dt=\int\frac{2t}{(2t-1)(t+2)}dt=\frac{1}{5}\int\frac{2dt}{2t-1}+\frac{4}{5}\int\frac{dt}{t+2}=\frac{1}{5}ln|2t-1|+\frac{4}{5}ln|t+2|+C=\frac{1}{5}ln|2\sqrt{3x+1}-1|+\frac{4}{5}ln|\sqrt{3x+1}+2|+C[/latex]



[latex]\int\frac{dx}{\sqrt{e^{2x}+e^{x}+1}}=/t=e^{x}/=\int\frac{dt}{t\sqrt{t^{2}+t+1}}=/u=\frac{1}{t}/=-\int\frac{du}{\sqrt{u^{2}+u+1}}=-ln|u+\frac{1}{2}+\sqrt{u^{2}+u+1}|+C=-ln|e^{-x}+\frac{1}{2}+e^{-x}\sqrt{e^{2x}+e^{x}+1}|+C[/latex]


Sori kompa, al' sad je ispalo banalno do ibera. 8)
OK, sori! I Crni se nekad zariba! Embarassed








Sori kompa, al' sad je ispalo banalno do ibera. Cool


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Crni
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: muško
Sarma = la pohva - posuda
4 = 29 - 25
Lokacija: Zagreb
PostPostano: 13:06 pet, 3. 9. 2004    Naslov: Citirajte i odgovorite
Ispravak za onaj na prvi na početku topica:

[latex]\int\frac{dx}{cos^{2}xtgx}=\int\frac{dx}{cosx \cdot sinx}=2\int\frac{dx}{sin2x}=/t=2x/=\int\frac{dt}{sint}=ln|tg\frac{t}{2}|+C=ln|tgx|+C[/latex]
Ispravak za onaj na prvi na početku topica:



[Vrh]
Korisnički profil Pošaljite privatnu poruku
Ema
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 02. 2005. (12:44:59)
Postovi: (9C)16
Sarma = la pohva - posuda
6 = 6 - 0
PostPostano: 22:28 sub, 28. 5. 2005    Naslov: Citirajte i odgovorite
moze malo objasnjenje vezano uz drugi zadatak, imamo
S dt/(t*sqrt(t^2+t+1) =/uzmemo supstituciju u=1/t, i imamo du=ln|t|*dt; dt=du/ln|t|=-du/ln|u| /= -s du/(lnu*sqrt(u^2+u+1))
je li se taj ln u rjesenju negdje izbgubio ili sam ja negdje pogresila?
moze malo objasnjenje vezano uz drugi zadatak, imamo
S dt/(t*sqrt(t^2+t+1) =/uzmemo supstituciju u=1/t, i imamo du=ln|t|*dt; dt=du/ln|t|=-du/ln|u| /= -s du/(lnu*sqrt(u^2+u+1))
je li se taj ln u rjesenju negdje izbgubio ili sam ja negdje pogresila?


[Vrh]
Korisnički profil Pošaljite privatnu poruku
vsego
Site Admin
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: zombi
Sarma = la pohva - posuda
854 = 1068 - 214
Lokacija: /sbin/init
PostPostano: 2:40 ned, 29. 5. 2005    Naslov: Citirajte i odgovorite
[quote="Ema"]moze malo objasnjenje vezano uz drugi zadatak, imamo
S dt/(t*sqrt(t^2+t+1) =/uzmemo supstituciju [color=red]u=1/t, i imamo du=ln|t|*dt[/color]; dt=du/ln|t|=-du/ln|u| /= -s du/(lnu*sqrt(u^2+u+1))
je li se taj ln u rjesenju negdje izbgubio ili sam ja negdje pogresila?[/quote]

Ovo crveno - cini mi se da si integrirala, umjesto da deriviras. :)

Tj. ako je u = 1/t, onda je du = -dt/t^2. 8)
Ema (napisa):
moze malo objasnjenje vezano uz drugi zadatak, imamo
S dt/(t*sqrt(t^2+t+1) =/uzmemo supstituciju u=1/t, i imamo du=ln|t|*dt; dt=du/ln|t|=-du/ln|u| /= -s du/(lnu*sqrt(u^2+u+1))
je li se taj ln u rjesenju negdje izbgubio ili sam ja negdje pogresila?


Ovo crveno - cini mi se da si integrirala, umjesto da deriviras. Smile

Tj. ako je u = 1/t, onda je du = -dt/t^2. Cool



_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. Drzim prodike
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2 Vremenska zona: GMT + 01:00.
Stranica 1 / 1.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan