|
Valjda ovo:
[latex]\int_{-\infty}^{\infty}e^{-x^2+4x}\,dx[/latex]
Mislim pa to je trivijalno ako znaš (npr. s UVIS-a) super-poznatu formulu:
[latex]\int_{-\infty}^{\infty}e^{-t^2}\,dt=\sqrt{\pi}[/latex]
Treba samo napraviti supstituciju t=x-2 i dobiješ rješenje [latex]e^4 \sqrt{\pi}[/latex]
-----------------
Inače, to nije tip integrala koji se tipično rješava pomoću teorema o reziduumima.
Gornja formula se dokazuje (npr. na UVIS-u ako se dobro sjećam) tako da se lijevi integral kvadrira, shvati kao dvostruki integral (tj. po R^2), a onda prijeđe na polarne koordinate.
Vjerujem da je na pismenima ne treba dokazivati jer je stvarno poznata. (Npr. pogledaj funkciju Erf u Mathematici.)
Valjda ovo:
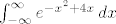
Mislim pa to je trivijalno ako znaš (npr. s UVIS-a) super-poznatu formulu:
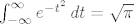
Treba samo napraviti supstituciju t=x-2 i dobiješ rješenje 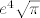
-----------------
Inače, to nije tip integrala koji se tipično rješava pomoću teorema o reziduumima.
Gornja formula se dokazuje (npr. na UVIS-u ako se dobro sjećam) tako da se lijevi integral kvadrira, shvati kao dvostruki integral (tj. po R^2), a onda prijeđe na polarne koordinate.
Vjerujem da je na pismenima ne treba dokazivati jer je stvarno poznata. (Npr. pogledaj funkciju Erf u Mathematici.)
|





