Zadaci s rekurzijama

[Ashley]

Moze li mi netko rijesiti ovu rekurziju
a_n+2 = (a_n+1)^3 / (a_n)^2

uz uvjete a_0 = 1 i a_1 = 2 ?
Hvala!

(Zadatak s roka M. Krnica)

[Gost]

To ti se logaritmira (tj ln) i onda se stavi b_n= ln(a_n) i normalno rješavaš rekurziju i rješenje vratiš u supstituciju. Meni je rješenje ispalo b_n=2^n-1, pa ti a_n=2^(2^n-1). (Tj. dva na potenciju od dva na n minus jedan.)

[Gost]

Ja ne znam rješiti ove rekurzije. Ima li nekog tko zna?
(30.09.2003. M.K.)
5. Niz (a_n) zadan je rekurzivnom relacijom a_0=m, a_n=-m/n(a_0+a_1+...+a_n-1) gdje je m zadani prirodan broj. Izračunajte sumu (2^0a_0+2^1a_1+...+2^ma_m)

(04.02.2004. M.K.)
4. Koliko se riječi duljine n može sastaviti od triju slova A, B i C tako da riječ počinje i završava slovom A, te da nikoja dva susjedna slova u riječi nisu jednaka. (nisam ni sigurna da to ide na rekurziju)

(30.09.2003.M.K.)
3. Neka je S n-člani skup. Nađite broj uređenih parova (X,Y) za koje vrijedi: X, Y su podskupovi od S, presjek im je prazan skup i |X|>3, |Y|>4 (ovo znam da se ne rješava pomoću rekurzije ali ga svejedno neznam rješiti).

[krcko]

[Gost]

Ovako kaze:
Imamo neN kuna. Svakog dana kupujemo točno jednu od 7 vrsta slatkiša: Pez Bombone (1 kuna), Bananko (1 kuna), Čunga Lunga (1 kuna), Tortica (2 kune), Cedevita bomboni (2 kune), Rum pločice (2 kune), Orbit (2 kune). Neka je M_n broj načina na koje možemo potrošiti n kuna na opisani način. Odredite rekurzivnu relaciju za M_n!

Zna li tko ovo riješiti?

[defar]

hm...pa, ako imas jednu kunu vise nego prije, mozes si ili nadokupit nesto sto kosta jednu kn (vidi koliko mogucnosti imas za to - cunga-lunga i jos nesto), ili izbacit' nesto sto si kupio za jednu kn i s ovom dodatnom kunom kupit nesto sto kosta dvije (bananka, zivotinjsko...kolko vec toga ima).

daklem, s jednu kn mozes potrosit' na 3 nacina (kupit jedno od tri stvari koje kostaju 1 kn).
a_1=3

s dvije kune mozes ili kupit dvije stvari po 1 kn (3 povrh 2) ili jednnu od 4 stvari koje kostaju 2 kn.

a_2=4+3=7

a_n=3*a_n-1 + 4*a_n-2


na a_n nacina mozes potrositi n kn

_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'

[vsego]

Ako kupujem dvije stvari po kunu, onda to valjda mogu izvesti na 6 nacina, a ne na 3.

Sama relacija mi se cini ok.

Btw, goste, u skladu s uputama, ovdje bas nisu dobrodosli postovi tipa "Rijesite mi zadatak...".

_________________
U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.

[krcko]

A osim toga je pozeljno ne otvarati novi topic ako vec postoji slican. Prethodna tri posta mergah iz topica pod nazivom 'Zadatak s rekurzijom'.

_________________
Vedran Krcadinac

Ljudi su razliciti, a nula je paran broj.

[pefri]

Napišite rekurzivnu relaciju za broj razlicitih particija n-članog skupa.

Zna li tko ovo rijesiti?

[@#]

[Gost]

Moze li mi netko objasniti kako doci do rekurzije u slijedecem zadatku?

Za n koji je prirodan broj, odredi broj nizova duljine n, sastavljenih od
elemenata skupa {0, 1, 2, 3}, tako da 1 i 2 nisu susjedni.

HVALA!

[defar]

nek je a_n koliko ima trazenih nizova duljine n.
jednoclanih nizova sa zadanim svojstvom ocito ima 4, nema uopce dva clana niza, pa nema ni dva susjedna. tj. a_1=4
a_2=12 jer ako niz pocinje s 3 ili 4, na drugome mjestu moze stajati bilo koji element skupa [4], a ako niz pocinje s jedan ili dva, na drugome mjestu mogu stajati ili 3 ili 4. to je 2*4+2*2=12 izgleda niza.

sad, ako ides slagati niz duljine n sa zadanim svojstvima, i na prvo mjesto stavis 1 ili 2, onda na drugome mjestu mora stajati ili 3 ili 4 (to je ukupno 4 kombinacije za prva dva clana niza : (1,3), (1,4), (2,3), (2,4)), a preostalih n-2 clanova niza mozes odabrati bilo kako, samo da nema susjednih dvojki-jedinica, a to mozes na a_n-2 nacina.

ako pak na prvo mjesto n-clanog niza stavis 3 ili 4, onda na preostalih n-1 mjesto mozes nadopisati bilo koji (n-1) -clani niz sa propisanim svojstvima, a njih ima a_n-1.

ovime su opisani svi moguci oblici n-cl niza, i svaki je pobrojan samo jednom (ne moze isti niz pocinjati i s 1 i s 3, naprimjer),
pa za niz (a_n)_neIN vrijedi rekurzivna relacija:

a_n=4*a_n-2+2*a_n-1

_________________
`To begin with, a dog's not mad. You grant that? 'Well, then,' the Cat went on, `you see, a dog growls when it's angry, and wags its tail when it's pleased. Now I growl when I'm pleased, and wag my tail when I'm angry. Therefore I'm mad.'

[hermione]

Ima problema sa jednom rekurzojim...Nikako ne mogu naci rjesenje karakteristicne jednadzbe pa ako mi neko moze pomoci....
Rekurzija glasi:
a_n=a_n-1 -2a_n-2 +4a_n-3
Pokusala sam sa djeliteljima slobodnog clana,ali me nije nigdje dovelo,zatim razne probe faktoriziranja,ali nista.....Lijena sam numerickom metodom pokusati.....

[vjekovac]

Karakteristična jednadžba x^3-x^2+2x-4=0 nema lijepe korijene (npr. ukucaj u Mathematicu Solve[x^3 - x^2 + 2x - 4 == 0, x] i uživaj. Pojavljuje se .)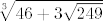
Ne znam kakva bi bila korist od numeričkog rješavanja ali korijeni su joj približno (jedan realni i dva prava kompleksna):

alfa1=1.477967243009012474646925
alfa2=-0.238983621504506237323462 - 1.62766911780350485424881450 i
alfa3=-0.238983621504506237323462 + 1.62766911780350485424881450 i

Međusobno su različiti pa je rješenje oblika
a_n=A*(alfa_1)^n+B*(alfa_2)^n+C*(alfa_3)^n
za neke koeficijente A,B,C koji se odrede iz početnih uvjeta.

Mislim da se rješenje ne može ljepše zapisati.
Ipak, ako su početni uvjeti "naštimani", moguće je da opći član niza ipak ima lijepu formulu (premda u ovom slučaju baš i ne vjerujem da ima).

[krcko]

Ako se dobro sjecam rekurzija se gledala modulo 3.

_________________
Vedran Krcadinac

Ljudi su razliciti, a nula je paran broj.

[hermione]

Ne razumijem.....Sta se misli pod time iliti kako se to rjesava rekurzija modulo 3?

[krcko]

Zadatak na koji mislim bio je na roku 21.6.2004. i glasi ovako:

[hermione]

Odrediti FI niza zadanog rekurzijom
(n+2)a_n+2=a_n+1+a_n,a0=a1=1

Pokusala sam to prvo srediti.Stavila sam supstituciju b_n=n*a_n i time dobila b_n+2=b_n+1/(n+1) + b_n/n....I tu sam zapela,ne cini mi se kao lijepi izraz za baratati.....Se more to nekak drukcije rijesiti ili se po tome kemija nekako?Help,pls.....

[krcko]

Probaj direktno iz rekurzije izvesti diferencijalnu jednadzbu koju mora zadovoljavati FI. For the record, ovo je 5. zadatak na roku 28.9.2004.

_________________
Vedran Krcadinac

Ljudi su razliciti, a nula je paran broj.

[hermione]

Evo ja sam to ovako,ali ne znam dal je to O.K.Vjerojatno nije, pa pls ispravak ako moze....

Prvo sam niz zapisala u oblik kojem je meni ipak lakse baratati...n*a_n=a_n-1+a_n-2.Mnozenjem sa x^n i sumiranjem po n sam dobila :sum n*a_n*x^n=sum a_n-1*x_n + sum a_n-2*x_n.To je jednako sada: x*a`(x)=x*a(x)+x^2*a(x).Podijelim sa x, separiram varijable i integriram i dobijem a(x)=e^(x+(x^2)/2))