| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 19:01 uto, 14. 6. 2005 Naslov: Nejasnoce vezane uz neprekidnost derivacije. Postano: 19:01 uto, 14. 6. 2005 Naslov: Nejasnoce vezane uz neprekidnost derivacije. |
    |
|
|
Recimo da imamo funciju f : I -> R koja je neprekidna na I.
I postoji neki inteval <a, b> podskup od I na kojem je f diferencijabilna.
Sada uzmem neki y iz <a, b>. Tada za svaki x iz <a, y> vrijedi po Lagrangeovom teoremu:
[latex]\frac{f(y) - f(x)}{y - x}=f'(x_c)[/latex], gdje je [latex]x<x_c<y[/latex]
Eh sad
[latex]\displaystyle \lim_{x\rightarrow y}\frac{f(y) - f(x)}{y - x}=f'(y)[/latex]
A
[latex]\displaystyle \lim_{x \rightarrow y}f'(x_c) = \lim_{x_c \rightarrow y}f'(x_c)[/latex]
Ne bi li sada trebalo slijediti da postoji [latex]\displaystyle \lim_{x \rightarrow y}f'(x)[/latex] i jednak je [latex]f'(y)[/latex]?
Znam da tome nije tako, jer bi ovo znacilo da derivacija mora biti neprekidna, ali gdje je greska :( :grrr: :sherlock:
Recimo da imamo funciju f : I → R koja je neprekidna na I.
I postoji neki inteval <a, b> podskup od I na kojem je f diferencijabilna.
Sada uzmem neki y iz <a, b>. Tada za svaki x iz <a, y> vrijedi po Lagrangeovom teoremu:
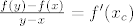 , gdje je , gdje je 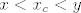
Eh sad
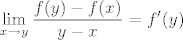
A
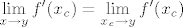
Ne bi li sada trebalo slijediti da postoji 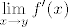 i jednak je i jednak je 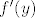 ? ?
Znam da tome nije tako, jer bi ovo znacilo da derivacija mora biti neprekidna, ali gdje je greska   
_________________
Bri
|
|
| [Vrh] |
|
goc9999
Forumaš(ica)


Pridružen/a: 15. 10. 2003. (19:31:20)
Postovi: (238)16
Spol: 
Lokacija: Utrina
|
 Postano: 20:05 uto, 14. 6. 2005 Naslov: Postano: 20:05 uto, 14. 6. 2005 Naslov: |
    |
|
|
diferencijabilnost => neprekidnost !
1.def. kaze: kazemo da je f diferencijabilna (f:I->R, I otvr.int. podskup od R) u tocki c od I, ako postoji lim[size=9]x->c[/size][f(x)-f(c)/x-c] i tada pisemo
f'(c)=lim[size=9]x->c[/size][f(x)-f(c)/x-c]
dok lang.tm. kaze: NEKA je f diferencijabilna (f:I->R, I otvr.int. podskup od R) i a<b (€ I). Tada POSTOJI c € <a,b> t.d. f(b)-f(a)=f'(c)(b-a).
def. kaze ako je funkcija diferenc => onaj limes
tm. kaze NEKA je f diferenc. => vrijedi onaj limes na domeni ( I ) od f => vrijedi i na <a,b> € I, tu se zapravo govori da je sekanta (u a i b) paralelna sa tangentom u c pa otud i f(b)-f(a)=f'(c)(b-a). vidi razliku uvjeta lang. tm i f:[a,b]->R (ona je neprekidna i diferencijabilna na <a,b>)
diferencijabilnost ⇒ neprekidnost !
1.def. kaze: kazemo da je f diferencijabilna (f:I→R, I otvr.int. podskup od R) u tocki c od I, ako postoji limx→c[f(x)-f(c)/x-c] i tada pisemo
f'(c)=limx→c[f(x)-f(c)/x-c]
dok lang.tm. kaze: NEKA je f diferencijabilna (f:I→R, I otvr.int. podskup od R) i a<b (€ I). Tada POSTOJI c € <a,b> t.d. f(b)-f(a)=f'(c)(b-a).
def. kaze ako je funkcija diferenc ⇒ onaj limes
tm. kaze NEKA je f diferenc. ⇒ vrijedi onaj limes na domeni ( I ) od f ⇒ vrijedi i na <a,b> € I, tu se zapravo govori da je sekanta (u a i b) paralelna sa tangentom u c pa otud i f(b)-f(a)=f'(c)(b-a). vidi razliku uvjeta lang. tm i f:[a,b]→R (ona je neprekidna i diferencijabilna na <a,b>)
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 20:44 uto, 14. 6. 2005 Naslov: Postano: 20:44 uto, 14. 6. 2005 Naslov: |
    |
|
|
Nisam bas siguran da sam skuzio u cemu je tocno problem, ali ako je problem u tome sto f nije diferencijabilna na cijeloj domeni, mozemo gledati restrikciju na <a, b> koja je diferencijabilna na cijeloj domeni.
Onda imamo f: <a, b> -> R, diferencijabilna => vrijedi limew => vrijedi i na <x, y> € <a, b>
Nisam bas siguran da sam skuzio u cemu je tocno problem, ali ako je problem u tome sto f nije diferencijabilna na cijeloj domeni, mozemo gledati restrikciju na <a, b> koja je diferencijabilna na cijeloj domeni.
Onda imamo f: <a, b> -> R, diferencijabilna => vrijedi limew => vrijedi i na <x, y> € <a, b>
_________________
Bri
|
|
| [Vrh] |
|
Stratos
Forumaš(ica)

Pridružen/a: 24. 03. 2004. (22:30:55)
Postovi: (7)16
|
 Postano: 22:06 uto, 14. 6. 2005 Naslov: Postano: 22:06 uto, 14. 6. 2005 Naslov: |
    |
|
|
urrm, sto znaci:
[latex]\displaystyle \lim_{x \rightarrow y}f'(x_c)[/latex]
?
mozda si pustio limes na jednakosti [latex]\displaystyle \frac{f(y) - f(x)}{y - x}=f'(x_c)[/latex]?
ta jednakost kaze npr. da je 3 = 3 (koliko vidim izraz s lijeve strane nije funkcija, jer smo fiksirali i x i y ~ to je samo neki broj). pustanje limesa je ... cudno :)
mozda si mislio na sljedece:
fiksiramo y, a zatim definiramo funkciju h sa domenom <a,b>\{y} koja za x iz <a,y> vraca neki x_c sa svojstvom [latex]\displaystyle \frac{f(y) - f(x)}{y - x}=f'(x_c)[/latex]. takodjer ako je x iz <y, b> ona opet vraca neki x_c' sa istim svojstvom.
sada pustimo limes kompozicije: [latex]\displaystyle \lim_{x \rightarrow y}f'(h(x)) = \lim_{x \rightarrow y} \left( {f' \circ h} \right)\left( x \right)[/latex]
~ to je slicno limesu na pocetku: [latex]\displaystyle \lim_{x \rightarrow y}f'(x_c)[/latex]
ocito h ide u y. no da bi limes kompozicije postojao mora postojati i limes f'(x) u tocki y, no to nam nitko ne garantira :)
urrm, sto znaci:
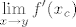
?
mozda si pustio limes na jednakosti 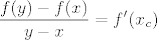 ? ?
ta jednakost kaze npr. da je 3 = 3 (koliko vidim izraz s lijeve strane nije funkcija, jer smo fiksirali i x i y ~ to je samo neki broj). pustanje limesa je ... cudno 
mozda si mislio na sljedece:
fiksiramo y, a zatim definiramo funkciju h sa domenom <a,b>\{y} koja za x iz <a,y> vraca neki x_c sa svojstvom 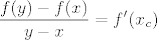 . takodjer ako je x iz <y, b> ona opet vraca neki x_c' sa istim svojstvom. . takodjer ako je x iz <y, b> ona opet vraca neki x_c' sa istim svojstvom.
sada pustimo limes kompozicije: 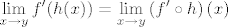
~ to je slicno limesu na pocetku: 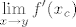
ocito h ide u y. no da bi limes kompozicije postojao mora postojati i limes f'(x) u tocki y, no to nam nitko ne garantira 
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
|
| [Vrh] |
|
|








