| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Ignavia
Forumaš(ica)
Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol: 
Lokacija: prijestolnica
|
 Postano: 15:28 uto, 14. 6. 2005 Naslov: fourierovi redovi |
    |
|
|
eh, sad, nije mi jasan dokaz konvergencije fourierovog reda za funkciju klase C2, tj što se dogodi nakon one dvije parcijalne integracije, a nije se moglo dogodit već nakon prve... zašto nismo mogli označiti sa M supremum |f'(x)|, i kako to točno integriramo nakon što uvedemo M, meni ispada da je integral jednak nuli zbog kosinusa...
prvo sam mislila da je potrebna druga derivacija zato što nam se to s nulom dogodi kad uvedemo M za prvu derivaciju (ovaj put zbog sinusa), al kad sam probala za kosinus i isto dobila 0, posumnjala sam u sve...
:scared: :znoj:
eh, sad, nije mi jasan dokaz konvergencije fourierovog reda za funkciju klase C2, tj što se dogodi nakon one dvije parcijalne integracije, a nije se moglo dogodit već nakon prve... zašto nismo mogli označiti sa M supremum |f'(x)|, i kako to točno integriramo nakon što uvedemo M, meni ispada da je integral jednak nuli zbog kosinusa...
prvo sam mislila da je potrebna druga derivacija zato što nam se to s nulom dogodi kad uvedemo M za prvu derivaciju (ovaj put zbog sinusa), al kad sam probala za kosinus i isto dobila 0, posumnjala sam u sve...
 
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)
Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
| Postano: 0:06 sri, 15. 6. 2005 Naslov: |
|
|
|
Inače, teorem vrijedi i općenitije (uz klasične [i]Dirichletove uvjete[/i] na funkciju), ali bez pretpostavke npr. da je funkcija C^2 je dokaz puno teži.
Pretpostavljam da je riječ o istom dokazu koji je u knjizi prof.Kurepe.
Dakle, imamo 2pi-periodičnu f-ju f:R->R koja je klase C^2 i neka su a_k, b_k Fourierovi koeficijenti. Neka je M supremum od |f''(x)|.
Dvostruka parcijalna integracija daje:
[latex]a_k=-\frac{1}{k^2 \pi}\int_{-\pi}^{\pi}f''(x)\cos kx \,dx[/latex]
pa je
[latex]|a_k|\leq\frac{1}{k^2 \pi}\int_{-\pi}^{\pi}|f''(x)|\cdot|\cos kx| \,dx\leq\frac{M\cdot 1\cdot 2\pi}{k^2 \pi}=\frac{2M}{k^2}[/latex]
Ovaj [latex]2\pi[/latex] se pojavio kao duljina intervala [latex][-\pi,\pi][/latex].
Primijeti da je cos unutar apsolutne vrijednosti pa integral [latex]\int_{-\pi}^{\pi}|\cos kx| \,dx[/latex] nije 0. Mogli bismo ga baš izračunati, ali nije bitno: koristimo samo da je [latex]\leq 2\pi[/latex].
Analogno se ocijeni b_k.
Sada je jasno da Fourierov red apsolutno (a u ovom slučaju čak i uniformno) konvergira (prema kriteriju o uspoređivanju) jer mu za članove vrijedi:
[latex]|a_k \cos kx| \leq 2M\cdot \frac{1}{k^2}[/latex]
[latex]|b_k \sin kx| \leq 2M\cdot \frac{1}{k^2}[/latex]
a za red [latex]\sum\frac{1}{k^2}[/latex] znamo da konvergira.
Nakon samo jedne parcijalne integracije (i uz oznaku M je sup od |f'(x)|) bismo Fourierov red ocijenili s harmonijskim redom [latex]\sum\frac{1}{k}[/latex], a on divergira pa to za Fourierov red baš ništa ne znači.
A npr. nakon tri parcijalne integracije (i uz oznaku M je sup od |f'''(x)|) bismo Fourierov red ocijenili s redom [latex]\sum\frac{1}{k^3}[/latex] pa bismo opet dobili apsolutnu konvergenciju, ali sada trebamo da je funkcija čak klase C^3.
Zato je optimalno dvaput parcijalno. 8)
Inače, teorem vrijedi i općenitije (uz klasične Dirichletove uvjete na funkciju), ali bez pretpostavke npr. da je funkcija C^2 je dokaz puno teži.
Pretpostavljam da je riječ o istom dokazu koji je u knjizi prof.Kurepe.
Dakle, imamo 2pi-periodičnu f-ju f:R→R koja je klase C^2 i neka su a_k, b_k Fourierovi koeficijenti. Neka je M supremum od |f''(x)|.
Dvostruka parcijalna integracija daje:
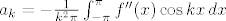
pa je
Ovaj 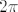 se pojavio kao duljina intervala  .
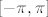Primijeti da je cos unutar apsolutne vrijednosti pa integral 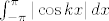 nije 0. Mogli bismo ga baš izračunati, ali nije bitno: koristimo samo da je  .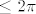
Analogno se ocijeni b_k.
Sada je jasno da Fourierov red apsolutno (a u ovom slučaju čak i uniformno) konvergira (prema kriteriju o uspoređivanju) jer mu za članove vrijedi:
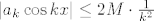
a za red 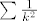 znamo da konvergira.
Nakon samo jedne parcijalne integracije (i uz oznaku M je sup od |f'(x)|) bismo Fourierov red ocijenili s harmonijskim redom 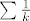 , a on divergira pa to za Fourierov red baš ništa ne znači.
A npr. nakon tri parcijalne integracije (i uz oznaku M je sup od |f'''(x)|) bismo Fourierov red ocijenili s redom 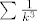 pa bismo opet dobili apsolutnu konvergenciju, ali sada trebamo da je funkcija čak klase C^3.
Zato je optimalno dvaput parcijalno. 
|
|
| [Vrh] |
|
Ignavia
Forumaš(ica)
Pridružen/a: 02. 10. 2004. (19:22:39)
Postovi: (235)16
Spol:
Lokacija: prijestolnica
|
|
| [Vrh] |
|
g o s t
Gost
|
|
| [Vrh] |
|
Grga
Forumaš(ica)
Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol:
|
|
| [Vrh] |
|
g o s t
Gost
|
|
| [Vrh] |
|
|
Puno hvala.