| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pbanicev
Forumaš(ica)

Pridružen/a: 23. 10. 2004. (19:32:44)
Postovi: (52)16
Spol: 
Lokacija: /dev/random V /dev/null V /dev/zero
|
|
| [Vrh] |
|
shokre
Forumaš(ica)


Pridružen/a: 11. 05. 2003. (20:05:09)
Postovi: (4A)16
Spol: 
|
 Postano: 12:24 pet, 24. 6. 2005 Naslov: Re: prekidnost i neprekidnost u točki grafa funkcije Postano: 12:24 pet, 24. 6. 2005 Naslov: Re: prekidnost i neprekidnost u točki grafa funkcije |
    |
|
|
[quote="pbanicev"]neka je npr. zadana funkcija: [latex]f(x):(I\subseteq{\bf R})\rightarrow{\bf R}.[/latex]
[latex]f(x)=\frac{1}{x} , za \hspace{1ex} x\in {\bf Q} ,[/latex]
[latex]f(x)=0 , za \hspace{1ex} x\in {\bf R}\setminus{\bf Q}[/latex].
kako pokazati, naravno ako je to točno, da funkcija ima prekid u svakoj
racionalnoj točki a neprekidna je u svakoj iracionalnoj točki.[/quote]
Ja bi rekao da je funkcija neprekidna u svakoj tocki iz domene.
U svakoj okolini svake tocke iz Q postoji tocka iz R/Q. Isto tako, u svakoj okolini tocke iz R/Q postoji tocka iz Q.
Dakle, ako izaberes neki x0 iz Q i izaberesh okolinu oko tocke f(x0)=1/x0 radijusa f(x0)/2 = (1/x0)/2, neces moci naci okolinu oko tocke x0 koja ce se cijela preslikati u tu tvoju izabranu okolinu. Jer koju god okolinu da uzmes, u njoj ce biti tocka iz R/Q, u kojoj je vrijednost funkcije 0, a mi smo uzeli bas takvu okolinu oko f(x0) (radijusa f(x0)/2) koja ne sadrzi nulu.
Ista prica ti je ako uzmes x0 iz R/Q, samo sto ce ti onda svaka okolina oko x0 sadrzavati tocku iz Q, koja ce ti pobjeci iz iste okoline (radijusa f(x0)/2).
| pbanicev (napisa): | neka je npr. zadana funkcija: 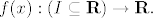
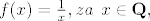
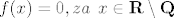 . .
kako pokazati, naravno ako je to točno, da funkcija ima prekid u svakoj
racionalnoj točki a neprekidna je u svakoj iracionalnoj točki. |
Ja bi rekao da je funkcija neprekidna u svakoj tocki iz domene.
U svakoj okolini svake tocke iz Q postoji tocka iz R/Q. Isto tako, u svakoj okolini tocke iz R/Q postoji tocka iz Q.
Dakle, ako izaberes neki x0 iz Q i izaberesh okolinu oko tocke f(x0)=1/x0 radijusa f(x0)/2 = (1/x0)/2, neces moci naci okolinu oko tocke x0 koja ce se cijela preslikati u tu tvoju izabranu okolinu. Jer koju god okolinu da uzmes, u njoj ce biti tocka iz R/Q, u kojoj je vrijednost funkcije 0, a mi smo uzeli bas takvu okolinu oko f(x0) (radijusa f(x0)/2) koja ne sadrzi nulu.
Ista prica ti je ako uzmes x0 iz R/Q, samo sto ce ti onda svaka okolina oko x0 sadrzavati tocku iz Q, koja ce ti pobjeci iz iste okoline (radijusa f(x0)/2).
_________________
~ Those who fear the Darkness have never seen what the Light can do! ~
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
pbanicev
Forumaš(ica)

Pridružen/a: 23. 10. 2004. (19:32:44)
Postovi: (52)16
Spol: 
Lokacija: /dev/random V /dev/null V /dev/zero
|
|
| [Vrh] |
|
shokre
Forumaš(ica)


Pridružen/a: 11. 05. 2003. (20:05:09)
Postovi: (4A)16
Spol: 
|
 Postano: 16:05 pet, 24. 6. 2005 Naslov: Re: prekidnost i neprekidnost u točki grafa funkcije Postano: 16:05 pet, 24. 6. 2005 Naslov: Re: prekidnost i neprekidnost u točki grafa funkcije |
    |
|
|
[quote="shokre"]Ja bi rekao da je funkcija [b]neprekidna[/b] u svakoj tocki iz domene.[/quote]
Tu sam naravno mislio da je funkcija [b]prekidna[/b] u svakoj tocki domene :? :oops:
[quote="pbanicev"]dakle, radi se o jednoj jedinoj funkciji. :idea:
[latex]f(x)=\begin{array}{rcl}\frac{1}{n} & \mbox{ako je} & x\in {\bf Q}\\0 & \mbox{ako je} & x\in {\bf R}\setminus{\bf Q}\end{array}[/latex][/quote]
Jesi sad fulao ovo 1/n ili se to htjelo reci da je funkcija u tockama iz Q konstantna i razlicita od 0?
Kako god da bilo, objasnjenje je isto, osim sto je ovako funkcija dobro definirana svugdje. E sad, da sam Hans, onda bi jos malo cjepidlacio da je bitno sto je "n"... :)
| shokre (napisa): | | Ja bi rekao da je funkcija neprekidna u svakoj tocki iz domene. |
Tu sam naravno mislio da je funkcija prekidna u svakoj tocki domene  
| pbanicev (napisa): | dakle, radi se o jednoj jedinoj funkciji. 
 |
Jesi sad fulao ovo 1/n ili se to htjelo reci da je funkcija u tockama iz Q konstantna i razlicita od 0?
Kako god da bilo, objasnjenje je isto, osim sto je ovako funkcija dobro definirana svugdje. E sad, da sam Hans, onda bi jos malo cjepidlacio da je bitno sto je "n"... 
_________________
~ Those who fear the Darkness have never seen what the Light can do! ~
|
|
| [Vrh] |
|
pbanicev
Forumaš(ica)

Pridružen/a: 23. 10. 2004. (19:32:44)
Postovi: (52)16
Spol: 
Lokacija: /dev/random V /dev/null V /dev/zero
|
|
| [Vrh] |
|
pbanicev
Forumaš(ica)

Pridružen/a: 23. 10. 2004. (19:32:44)
Postovi: (52)16
Spol: 
Lokacija: /dev/random V /dev/null V /dev/zero
|
 Postano: 17:36 pet, 24. 6. 2005 Naslov: Postano: 17:36 pet, 24. 6. 2005 Naslov: |
    |
|
|
ah pa da :!: izvolite pogledajte link :arrow: http://planetmath.org/encyclopedia/DirichletsFunction.html
funkcija o kojoj sam pisao zove se Dirichletova funkcija (u vecoj ili manjoj mjeri, vidljive su neke razlike u definiciji, prije bi se možda radilo o kompoziciji) 8)
dakle, moje mišljenje pada u vodu, ipak postoji takva funkcija, :o
i izgleda da nije kontradiktorna sa primjerom na predavanjima, najvjerojatnije se radi o krivoj informaciji da je "takva" funkcija prekidna u svakoj točki.
no kako iz definicije neprekidnosti funkcije i ostalih aksioma polja R to doista pokazati. :crazyeyes:
ah pa da  izvolite pogledajte link izvolite pogledajte link  http://planetmath.org/encyclopedia/DirichletsFunction.html http://planetmath.org/encyclopedia/DirichletsFunction.html
funkcija o kojoj sam pisao zove se Dirichletova funkcija (u vecoj ili manjoj mjeri, vidljive su neke razlike u definiciji, prije bi se možda radilo o kompoziciji) 
dakle, moje mišljenje pada u vodu, ipak postoji takva funkcija, 
i izgleda da nije kontradiktorna sa primjerom na predavanjima, najvjerojatnije se radi o krivoj informaciji da je "takva" funkcija prekidna u svakoj točki.
no kako iz definicije neprekidnosti funkcije i ostalih aksioma polja R to doista pokazati. 
|
|
| [Vrh] |
|
|











