|
[quote="mandark"][color=red]Prop 4.5[/color]
Neka su ([color=red]e[/color])=[latex](e_1,........,e_n)[/latex] , ([color=red]f[/color])=[latex](f_1,......,f_m)[/latex] , ([color=red]g[/color])=[latex](g_1,.....,g_l)[/latex] baze vektorskih prostora[b] V,W,X[/b] , neka je [color=blue]A[/color]e[b]L[/b](V,W) i [color=blue]B[/color]e[b]L[/b](W,X).
Tada je [color=blue]BA[/color]e[b]L[/b](V,X) i [color=blue]BA[/color]([color=red]g,e[/color]) = [b]B[/b]([color=red]g,f[/color])[b] A[/b]([color=red]f,e[/color]).
[b]DOKAZ:[/b]
BA je lin op. to je vec dokazano.
[latex]Neka je A(f,e) = (\alpha_{ij}) e M_{mn} i B(g,f) = (\beta_{ij}) e M_{lm} [/latex] [b]<--[/b]može li mi netko reći kako da interpretiram ovo
[/quote]
to znaci da je matrica A u paru baza[latex](e_k), (f_i)[/latex] mxn matrica kojoj je element na mjestu i,j [latex](\alpha_{ij})[/latex] Analogno za drugu matricu operatora.
Elementi matrice opisuju djelovanje operatora na elemente baze, i ono je ovakvo:
[latex]Av_k=\Sigma_{i=1}^m \alpha_{ik}f_i[/latex]
[latex]Bf_i=\Sigma_{j=1}^l \beta_{ji}g_j[/latex]
[quote="mandark"]I sada on raspisuje djelovanje operatora na bazu domene[latex] (e_k)[/latex]
[latex] BA(e_k)=B(A(e_k))=B(\Sigma_{i=1}^m \alpha_{ik} f_i) = \Sigma_{i=1}^m \alpha_{ik}B(f_i) = \Sigma_{i=1}^m \alpha_{ik} \Sigma_{j=1}^l \beta_{ji}g_j = \Sigma_{j=1}^l (\Sigma_{i=1}^m \beta_{ji}\alpha_{ik})g_j[/latex]
[/quote]
Tu smo vidjeli kako operator BA djeluje na elemente baze.
[latex]\Sigma_{i=1}^m \beta_{ji}\alpha_{ik} = [BA]_{jk}[/latex], tj. to je upravo matrica BA na mjestu jk.
To znaci da operator BA ovako djeluje na elemente baze: [latex]BA(e_k) = \Sigma_{j=1}^l [BA]_{jk}g_j[/latex]
Sada kada znas djelovanje operatora na bazu, onda znas i matricu linearnog operatora u danom paru baza, a po definiciji je njen element na mjestu j,k upravo [latex][BA]_{jk}[/latex]
Reci ako ti jos uvijek nije jasno :P
| mandark (napisa): | Prop 4.5
Neka su (e)= , (f)= , (f)=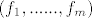 , (g)= , (g)=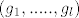 baze vektorskih prostora V,W,X , neka je AeL(V,W) i BeL(W,X). baze vektorskih prostora V,W,X , neka je AeL(V,W) i BeL(W,X).
Tada je BAeL(V,X) i BA(g,e) = B(g,f) A(f,e).
DOKAZ:
BA je lin op. to je vec dokazano.
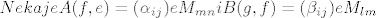 ←može li mi netko reći kako da interpretiram ovo ←može li mi netko reći kako da interpretiram ovo
|
to znaci da je matrica A u paru baza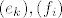 mxn matrica kojoj je element na mjestu i,j mxn matrica kojoj je element na mjestu i,j 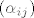 Analogno za drugu matricu operatora. Analogno za drugu matricu operatora.
Elementi matrice opisuju djelovanje operatora na elemente baze, i ono je ovakvo:
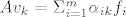
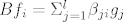
| mandark (napisa): | I sada on raspisuje djelovanje operatora na bazu domene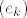
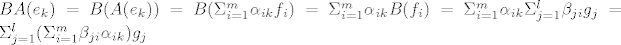
|
Tu smo vidjeli kako operator BA djeluje na elemente baze.
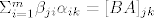 , tj. to je upravo matrica BA na mjestu jk. , tj. to je upravo matrica BA na mjestu jk.
To znaci da operator BA ovako djeluje na elemente baze: 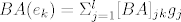
Sada kada znas djelovanje operatora na bazu, onda znas i matricu linearnog operatora u danom paru baza, a po definiciji je njen element na mjestu j,k upravo 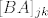
Reci ako ti jos uvijek nije jasno 
_________________
Bri
|







