|
[color=olive]NAPOMENA: SVE TeX greske uocljive dolje nisu greske u mom TeX kodu, vec greske u implenetaciji.[/color]
[color=darkred][b]Admin edit:[/b] Bilo je i tvojih gresaka, ali da - vecina je do implementacije. :( Pokusavam promijeniti neke stvari, pa ce implementacija TeXa u narednim danima malo šepati...[/color]
[quote="PITANJA ZA USMENI ISPIT IZ INTEGRALA I MJERE"]
[b]Osnovni koncepti[/b]
[b]1.[/b] Definiraj poluprsten, prsten, i [latex]\sigma [/latex]-algebru za familije skupova. Koja struktura implicira koju strukturu? Daj netrivijalan primjer poluprstena koji nije prsten, i prstena koji nije [latex]\sigma [/latex]-algebra.
[b]2.[/b] Koji su aksiomi mjere na [latex]\sigma [/latex]-algebri skupova? Daj bar 3 netrivijalna primjera. Kakav je odnos sa teorijom vjerojatnosti? Kada je mjera konačna, kada [latex]\sigma[/latex]-konačna, a kada potpuna?
[b]3.[/b] Zašto ne možemo konstruirati mjeru sa zadovoljavajućim svojstvima na partitivnom skupu od [latex]\mathbb{ R}[/latex] ? Objasni koja su to zadovoljavajuća svojstva, te razloge.
[b]4.[/b] Opiši tri osnovna koraka konstrukcije Lebesgueove mjere na familiji Lebesgueovih podskupova od [latex]\mathbb{ R}[/latex] mjera na poluprstenu, proširenje na prsten, te proširenje na [latex]\sigma [/latex]-algebru. Precizno izrazi nekoliko ključnih teorema u toj konstrukciji.
[b]5.[/b] Definiraj vanjsku mjeru. Daj osnovni primjer konstrukcije vanjske mjere, ako je zadana konačno aditivna funkcija na prstenu. Daj konkretni primjer!
[b]6.[/b] Precizno izreci Caratheodoryev teorem. Koji su glavni koraci dokaza?
[b]7.[/b] Definiraj potpuni prostor s mjerom. Daj netrivijalni primjer prostora s mjerom koji jest, i koji nije potpun. Definiraj [latex]\sigma[/latex]- konačan prostor s mjerom. Daj netrivijalni primjer prostora s mjerom koji jest, i koji nije [latex]\sigma[/latex]- konačan.
[b]8.[/b] Precizno izreci Hahnov teorem. Koji su glavni koraci dokaza?
[b]9.[/b] Definiraj izmjeriv prostor i izmjerivu funkciju između dva izmjeriva prostora. Ako su zadana dva topološka prostora [latex](A, \tau), (A', \tau')[/latex], te neprekidna funkcija [latex] f : (A, \tau) \to (A', \tau')[/latex]. Neka su [latex]F, F'[/latex] najmanje [latex]\sigma [/latex]-algebre koje sadrže [latex]\tau, \tau'[/latex] respektivno. Da li je [latex]f : (A, F) \to (A, F')[/latex] izmjeriva funkcija?
[b]10.[/b] Objasni osnovne korake definiranja integrala pozitivne realne izmjerive funkcije.
[b]11.[/b] Iskaži Lebesgueov teorem o monotonoj konvergenciji, i objasni osnovne korake dokaza.
[b]12.[/b] Iskaži Fatouovu lemu, i objasni osnove korake dokaza.
[b]13.[/b] Definiraj kada je izmjeriva funkcija (Lebesgue) integrabilna. Daj primjer funkcije koja nije integrabilna. Objasni zašto je realna Riemann-integrabilna funkcija [latex]f : \mathbb{ R} \to \mathbb{ R} [/latex] Lebesgue integrabilna.
[b]14.[/b] Iskaži Lebesgueov teorem o dominiranoj konvergenciji, i objasni osnovne korake dokaza.
[b]15.[/b] Napiši aksiome metričkog, normiranog i Banachovog prostora. U kakvom su odnosu? Daj primjer metričkog prostora koji nije normiran, i normiranog koji nije Banachov (uputa: svi primjeri mogu biti podskupovi od [latex]\mathbb{ R}[/latex]).
[b]16.[/b] Definiraj prostor [latex]L(X,\mathcal{ F}, \mu)[/latex], i skiciraj dokaz da je to normiran prostor.
[b]17.[/b] Definiraj prostor [latex]L_p(X,\mathcal{ F}, \mu)[/latex], i skiciraj dokaz da je to normiran prostor.
[b]18.[/b] Definiraj prostor [latex]L_p(X,\mathcal{ F}, \mu)[/latex], i objasni ideju dokaza (bez detalja) da je to potpun prostor, koristeći činjenicu da je normiran.
[b]19.[/b] Definiraj prostor [latex]L_\infty(X,\mathcal{ F}, \mu)[/latex], te pokaži iz definicije da je Banachov (bez detalja).
[b]20.[/b] Definiraj uniformnu konvergenciju, konvergenciju po točkama, konvergenciju skoro svuda, konvergenciju u [latex]L_p[/latex] , i konvergenciju po mjeri. Daj barem četiri primjera koji tip konvergencije implicira neki drugi tip konvergencije od tih pet (moguće uz neke uvjete).
[b]21.[/b] Definiraj uniformnu konvergenciju, konvergenciju po točkama, konvergenciju skoro svuda, konvergenciju u [latex]L_p[/latex] , i konvergenciju po mjeri. Daj barem četiri protuprimjera kada neki tip konvergencije ne implicira neki drugi tip konvergencije od tih pet.
[b]Tehnike integrala i mjere[/b]
[b]22.[/b] Neka je [latex]C[/latex] familija skupova. Neka je [latex]B[/latex] familija svih konačnih disjunktnih unija skupova iz [latex]C[/latex], te neka je [latex]A[/latex] familija svih konačnih unija skupova iz [latex]C[/latex]. Napiši ideju dokaza da je [latex]A=B=R(C)[/latex], gdje je [latex]R(C)[/latex] najmanji prsten koji sadrži [latex]C[/latex].
[b]23.[/b] Neka je [latex]\mu : P^1 \to [0,+\infty][/latex][latex]\sigma[/latex]-aditivna funkcija na [latex]P^1[/latex] , gdje je [latex]P^1[/latex] skup svih poluotvorenih intervala na [latex]\mathbb{ R}[/latex]. Dokaži da je njeno jedinstveno proširenje na prsten elementarnih skupova [latex]E[/latex] također [latex]\sigma[/latex]-aditivna funkcija.
[b]24.[/b] Skiciraj dokaz da je funkcija [latex]\mu^* : P(X)\to [0,+\infty] [/latex] definirana sa [latex]\mu^*(A)=\inf \left\{\sum\limits_{i=1}^n \mu(F_i) : F_i \in R \& A\subseteq\bigcup\limits_{i=1}^n F_i\right\}[/latex], je vanjska mjere, gdje je [latex]\mu[/latex] [latex]\sigma[/latex]-aditivna funkcija na prstenu [latex]R[/latex].
[b]25.[/b] Definiraj izmjeriv skup u odnosu na vanjsku mjeru. Objasni zašto je uvjet iz definicije ekvivalentan uvjetu [latex]\mu^*(A)\geq \mu^*(A\cap E) + \mu^*(A\backslash E)[/latex].
[b]26.[/b] Dokaži slijedeću tvrdnju: Neka je [latex]M[/latex] familija podskupova koji su izmjerivi u odnosu na vanjsku mjeru [latex]\mu^*[/latex]. Tada je [latex]M[/latex] zatvorena na prebrojive unije.
[b]27.[/b] Dokaži iz definicije da je Lebesgueova mjera invarijatna na translaciju.
[b]28.[/b] Dokaži da ako su [latex] f, g : X \to \hbox{\bf R}[/latex] izmjerive, da su i [latex]fg[/latex], [latex]f+g[/latex] izmjerive. Definiraj [latex] \lim\inf[/latex] . Dokaži da je [latex]\lim\inf[/latex] niza izmjerivih funkcija izmjeriva funkcija.
[b]29.[/b] Definiraj mjeru na izmjerivom prostoru. Dokaži da je neprekidna (i objasni što to znači)! Ako je zadana konačno aditivna funkcija na izmjerivom prostoru, da li mora biti neprekidna? Zašto?
[b]30.[/b] Izreci i dokaži tvrdnju da se svaka pozitivna realna izmjeriva funkcija može prikazati kao limes funkcija koje poprimaju konačno mnogo vrijednosti.
[b]31.[/b] Skiciraj dokaz, koristeći definiciju, da je integral jednostavne pozitivne realne izmjerive funkcije linearan. Koja je osnovna tehnička poteškoća u dokazu?
[b]32.[/b] Dokaži iz definicije da je integral pozitivne izmjerive funkcije monoton.
[b]33.[/b] Dokaži slijedeću tvrdnju pomoću Fatouove leme: ako je [latex]f[/latex] pozitivna realna izmjeriva funkcija, tada je [latex] {f(x) = 0} [/latex] [latex] \mu [/latex]-s.s. ako i samo ako je [latex]\int f d\mu = 0[/latex].
[b]34.[/b] Dokaži pomoću Lebesgueovog teorema o dominiranoj konvergenciji da ako je [latex]t\mapsto f(x,t)[/latex] neprekidna na intervalu [latex][a,b][/latex], i [latex]|f(x,t)| < g(x)[/latex] za neku integrabilnu funkciju [latex]g[/latex], da je tada funkcija [latex]t\mapsto \int f(x,t) d\mu[/latex] neprekidna na intervalu [latex][a,b][/latex].
[b]35.[/b] Objasni pomoću Lebesgueovog teorema o dominiranoj konvergenciji dovoljan uvjet kada možemo zamijeniti derivaciju i znak integrala.
[b]36.[/b] Skiciraj primjer skupa koji jest Lebesgue izmjeriv ali nije Borel izmjeriv. Obasni razliku skupa Borel izmjerivih i Lebesgue izmjerivih skupova na [latex] \mathbb{ R} [/latex].
[b]37.[/b] Dokaži da uniformna konvergencija funkcija u [latex]L_p[/latex] implicira konvergenciju u [latex] {L_{p}} [/latex].
[b]38.[/b] Dokaži da niz funkcija koji konvergira skoro svuda, dominiran u [latex]L_p[/latex], konvergira u [latex] {L_{p}} [/latex].
[b]39.[/b] Dokaži da konvergencija skoro svuda implicira konvergenciju po mjeri.
Na ispitu student odgovara dva pitanja iz poglavlja „Osnovni koncepti“, te jedno iz poglavlja „Tehnike integrala i mjere“.
Zagreb, 19. lipnja 2005.
Doc. dr. sc. Siniša Slijepčević
[/quote]
'ave fun!
Sinisa
NAPOMENA: SVE TeX greske uocljive dolje nisu greske u mom TeX kodu, vec greske u implenetaciji.
Admin edit: Bilo je i tvojih gresaka, ali da - vecina je do implementacije.  Pokusavam promijeniti neke stvari, pa ce implementacija TeXa u narednim danima malo šepati... Pokusavam promijeniti neke stvari, pa ce implementacija TeXa u narednim danima malo šepati...
| PITANJA ZA USMENI ISPIT IZ INTEGRALA I MJERE (napisa): |
Osnovni koncepti
1. Definiraj poluprsten, prsten, i  -algebru za familije skupova. Koja struktura implicira koju strukturu? Daj netrivijalan primjer poluprstena koji nije prsten, i prstena koji nije -algebru za familije skupova. Koja struktura implicira koju strukturu? Daj netrivijalan primjer poluprstena koji nije prsten, i prstena koji nije  -algebra. -algebra.
2. Koji su aksiomi mjere na  -algebri skupova? Daj bar 3 netrivijalna primjera. Kakav je odnos sa teorijom vjerojatnosti? Kada je mjera konačna, kada -algebri skupova? Daj bar 3 netrivijalna primjera. Kakav je odnos sa teorijom vjerojatnosti? Kada je mjera konačna, kada  -konačna, a kada potpuna? -konačna, a kada potpuna?
3. Zašto ne možemo konstruirati mjeru sa zadovoljavajućim svojstvima na partitivnom skupu od 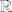 ? Objasni koja su to zadovoljavajuća svojstva, te razloge. ? Objasni koja su to zadovoljavajuća svojstva, te razloge.
4. Opiši tri osnovna koraka konstrukcije Lebesgueove mjere na familiji Lebesgueovih podskupova od 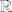 mjera na poluprstenu, proširenje na prsten, te proširenje na mjera na poluprstenu, proširenje na prsten, te proširenje na  -algebru. Precizno izrazi nekoliko ključnih teorema u toj konstrukciji. -algebru. Precizno izrazi nekoliko ključnih teorema u toj konstrukciji.
5. Definiraj vanjsku mjeru. Daj osnovni primjer konstrukcije vanjske mjere, ako je zadana konačno aditivna funkcija na prstenu. Daj konkretni primjer!
6. Precizno izreci Caratheodoryev teorem. Koji su glavni koraci dokaza?
7. Definiraj potpuni prostor s mjerom. Daj netrivijalni primjer prostora s mjerom koji jest, i koji nije potpun. Definiraj  - konačan prostor s mjerom. Daj netrivijalni primjer prostora s mjerom koji jest, i koji nije - konačan prostor s mjerom. Daj netrivijalni primjer prostora s mjerom koji jest, i koji nije  - konačan. - konačan.
8. Precizno izreci Hahnov teorem. Koji su glavni koraci dokaza?
9. Definiraj izmjeriv prostor i izmjerivu funkciju između dva izmjeriva prostora. Ako su zadana dva topološka prostora 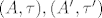 , te neprekidna funkcija , te neprekidna funkcija 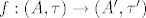 . Neka su . Neka su 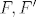 najmanje najmanje  -algebre koje sadrže -algebre koje sadrže 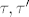 respektivno. Da li je respektivno. Da li je 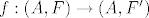 izmjeriva funkcija? izmjeriva funkcija?
10. Objasni osnovne korake definiranja integrala pozitivne realne izmjerive funkcije.
11. Iskaži Lebesgueov teorem o monotonoj konvergenciji, i objasni osnovne korake dokaza.
12. Iskaži Fatouovu lemu, i objasni osnove korake dokaza.
13. Definiraj kada je izmjeriva funkcija (Lebesgue) integrabilna. Daj primjer funkcije koja nije integrabilna. Objasni zašto je realna Riemann-integrabilna funkcija 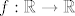 Lebesgue integrabilna. Lebesgue integrabilna.
14. Iskaži Lebesgueov teorem o dominiranoj konvergenciji, i objasni osnovne korake dokaza.
15. Napiši aksiome metričkog, normiranog i Banachovog prostora. U kakvom su odnosu? Daj primjer metričkog prostora koji nije normiran, i normiranog koji nije Banachov (uputa: svi primjeri mogu biti podskupovi od 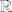 ). ).
16. Definiraj prostor 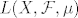 , i skiciraj dokaz da je to normiran prostor. , i skiciraj dokaz da je to normiran prostor.
17. Definiraj prostor 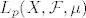 , i skiciraj dokaz da je to normiran prostor. , i skiciraj dokaz da je to normiran prostor.
18. Definiraj prostor 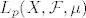 , i objasni ideju dokaza (bez detalja) da je to potpun prostor, koristeći činjenicu da je normiran. , i objasni ideju dokaza (bez detalja) da je to potpun prostor, koristeći činjenicu da je normiran.
19. Definiraj prostor 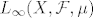 , te pokaži iz definicije da je Banachov (bez detalja). , te pokaži iz definicije da je Banachov (bez detalja).
20. Definiraj uniformnu konvergenciju, konvergenciju po točkama, konvergenciju skoro svuda, konvergenciju u 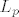 , i konvergenciju po mjeri. Daj barem četiri primjera koji tip konvergencije implicira neki drugi tip konvergencije od tih pet (moguće uz neke uvjete). , i konvergenciju po mjeri. Daj barem četiri primjera koji tip konvergencije implicira neki drugi tip konvergencije od tih pet (moguće uz neke uvjete).
21. Definiraj uniformnu konvergenciju, konvergenciju po točkama, konvergenciju skoro svuda, konvergenciju u 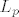 , i konvergenciju po mjeri. Daj barem četiri protuprimjera kada neki tip konvergencije ne implicira neki drugi tip konvergencije od tih pet. , i konvergenciju po mjeri. Daj barem četiri protuprimjera kada neki tip konvergencije ne implicira neki drugi tip konvergencije od tih pet.
Tehnike integrala i mjere
22. Neka je  familija skupova. Neka je familija skupova. Neka je  familija svih konačnih disjunktnih unija skupova iz familija svih konačnih disjunktnih unija skupova iz  , te neka je , te neka je  familija svih konačnih unija skupova iz familija svih konačnih unija skupova iz  . Napiši ideju dokaza da je . Napiši ideju dokaza da je 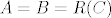 , gdje je , gdje je 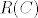 najmanji prsten koji sadrži najmanji prsten koji sadrži  . .
23. Neka je 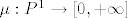  -aditivna funkcija na -aditivna funkcija na 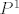 , gdje je , gdje je 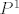 skup svih poluotvorenih intervala na skup svih poluotvorenih intervala na 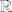 . Dokaži da je njeno jedinstveno proširenje na prsten elementarnih skupova . Dokaži da je njeno jedinstveno proširenje na prsten elementarnih skupova 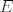 također također  -aditivna funkcija. -aditivna funkcija.
24. Skiciraj dokaz da je funkcija 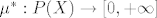 definirana sa definirana sa 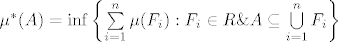 , je vanjska mjere, gdje je , je vanjska mjere, gdje je 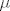  -aditivna funkcija na prstenu -aditivna funkcija na prstenu 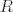 . .
25. Definiraj izmjeriv skup u odnosu na vanjsku mjeru. Objasni zašto je uvjet iz definicije ekvivalentan uvjetu  . .
26. Dokaži slijedeću tvrdnju: Neka je  familija podskupova koji su izmjerivi u odnosu na vanjsku mjeru familija podskupova koji su izmjerivi u odnosu na vanjsku mjeru 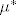 . Tada je . Tada je  zatvorena na prebrojive unije. zatvorena na prebrojive unije.
27. Dokaži iz definicije da je Lebesgueova mjera invarijatna na translaciju.
28. Dokaži da ako su 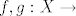 izmjerive, da su i izmjerive, da su i 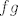 , ,  izmjerive. Definiraj izmjerive. Definiraj 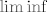 . Dokaži da je . Dokaži da je 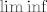 niza izmjerivih funkcija izmjeriva funkcija. niza izmjerivih funkcija izmjeriva funkcija.
29. Definiraj mjeru na izmjerivom prostoru. Dokaži da je neprekidna (i objasni što to znači)! Ako je zadana konačno aditivna funkcija na izmjerivom prostoru, da li mora biti neprekidna? Zašto?
30. Izreci i dokaži tvrdnju da se svaka pozitivna realna izmjeriva funkcija može prikazati kao limes funkcija koje poprimaju konačno mnogo vrijednosti.
31. Skiciraj dokaz, koristeći definiciju, da je integral jednostavne pozitivne realne izmjerive funkcije linearan. Koja je osnovna tehnička poteškoća u dokazu?
32. Dokaži iz definicije da je integral pozitivne izmjerive funkcije monoton.
33. Dokaži slijedeću tvrdnju pomoću Fatouove leme: ako je  pozitivna realna izmjeriva funkcija, tada je pozitivna realna izmjeriva funkcija, tada je 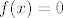 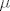 -s.s. ako i samo ako je -s.s. ako i samo ako je 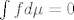 . .
34. Dokaži pomoću Lebesgueovog teorema o dominiranoj konvergenciji da ako je 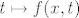 neprekidna na intervalu neprekidna na intervalu 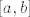 , i , i 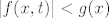 za neku integrabilnu funkciju za neku integrabilnu funkciju  , da je tada funkcija , da je tada funkcija 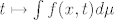 neprekidna na intervalu neprekidna na intervalu 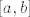 . .
35. Objasni pomoću Lebesgueovog teorema o dominiranoj konvergenciji dovoljan uvjet kada možemo zamijeniti derivaciju i znak integrala.
36. Skiciraj primjer skupa koji jest Lebesgue izmjeriv ali nije Borel izmjeriv. Obasni razliku skupa Borel izmjerivih i Lebesgue izmjerivih skupova na 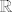 . .
37. Dokaži da uniformna konvergencija funkcija u 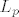 implicira konvergenciju u implicira konvergenciju u 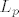 . .
38. Dokaži da niz funkcija koji konvergira skoro svuda, dominiran u 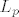 , konvergira u , konvergira u 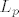 . .
39. Dokaži da konvergencija skoro svuda implicira konvergenciju po mjeri.
Na ispitu student odgovara dva pitanja iz poglavlja „Osnovni koncepti“, te jedno iz poglavlja „Tehnike integrala i mjere“.
Zagreb, 19. lipnja 2005.
Doc. dr. sc. Siniša Slijepčević
|
'ave fun!
Sinisa
_________________
Oslobodjen Senata.
|








