| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 18:47 pet, 19. 8. 2005 Naslov: Brainteaseri iz skripte prof Čaklovića Postano: 18:47 pet, 19. 8. 2005 Naslov: Brainteaseri iz skripte prof Čaklovića |
    |
|
|
[quote="Definicija 1.13 (1. poglavlje, strana 10.)"][b]Komponenta povezanosti[/b] C grafa G je maksimalan povezan podgraf od G u odnosu na relaciju ulaganja.
Pri tome je podgraf G' maksimalan u zadanoj familiji podgrafova, ovdje se radi o familiji povezanih podgrafova, ako za svaki podgraf G iz familije vrijedi da "G ulozen u G' " implicira G=G'[/quote]
o, recenicna konstrukcijo :(
| Definicija 1.13 (1. poglavlje, strana 10.) (napisa): | Komponenta povezanosti C grafa G je maksimalan povezan podgraf od G u odnosu na relaciju ulaganja.
Pri tome je podgraf G' maksimalan u zadanoj familiji podgrafova, ovdje se radi o familiji povezanih podgrafova, ako za svaki podgraf G iz familije vrijedi da "G ulozen u G' " implicira G=G' |
o, recenicna konstrukcijo 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
|
| [Vrh] |
|
anamari
Forumaš(ica)

Pridružen/a: 31. 03. 2003. (13:05:12)
Postovi: (E1)16
Spol: 
Lokacija: Here, there, everywhere...
|
|
| [Vrh] |
|
koryanshea
Forumaš(ica)


Pridružen/a: 12. 10. 2003. (23:50:23)
Postovi: (442)16
Spol: 
Lokacija: Bebop (converted interplanetary trawler)
|
 Postano: 16:51 ned, 21. 8. 2005 Naslov: Postano: 16:51 ned, 21. 8. 2005 Naslov: |
    |
|
|
ajde pliz reci nam sto je to komponenta povezanosti grafa, jer ovako mozemo samo nagadat da smo dobro pokopcali.
ajde pliz reci nam sto je to komponenta povezanosti grafa, jer ovako mozemo samo nagadat da smo dobro pokopcali.
_________________  "Download the files to a non-networked, firewalled computer."
- Dr. Elizabeth Weir |
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 23:28 ned, 21. 8. 2005 Naslov: Postano: 23:28 ned, 21. 8. 2005 Naslov: |
    |
|
|
Hvla vjekovac :D Pokusao sam ovako :)
[quote]Za familiju podgrafova nekog grafa G definiramo maksimalni podgraf Gmax za tu familiju ukoliko iz " Gmax ulozen u G' " slijedi Gmax=G'
Komponenta povezanosti C grafa G je maksimalni podgraf neke familije povezanih podgrafova od G.[/quote]
Hvla vjekovac  Pokusao sam ovako Pokusao sam ovako 
| Citat: | Za familiju podgrafova nekog grafa G definiramo maksimalni podgraf Gmax za tu familiju ukoliko iz " Gmax ulozen u G' " slijedi Gmax=G'
Komponenta povezanosti C grafa G je maksimalni podgraf neke familije povezanih podgrafova od G. |
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
 Postano: 1:24 pon, 22. 8. 2005 Naslov: Postano: 1:24 pon, 22. 8. 2005 Naslov: |
    |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"]
[quote]Za familiju podgrafova nekog grafa G definiramo maksimalni podgraf Gmax za tu familiju ukoliko iz " Gmax ulozen u G' " slijedi Gmax=G'
Komponenta povezanosti C grafa G je maksimalni podgraf neke familije povezanih podgrafova od G.[/quote][/quote]
skvik!
Komponenta povezanoti C grafa G je maksimalni podgraf familije [b]svih[/b] povezanih podgrafova od G.
Maksimalni element parc. uredjenog skupa nije nuzno jedinstven! Npr. imamo tri objekta, [latex]A[/latex], [latex]B[/latex] i [latex]C[/latex], te neka je relacija [latex]\geq[/latex] zadana sa [latex]A\geq C[/latex] i [latex]B\geq C[/latex], te [latex]x\geq x[/latex] za sve [latex]x\in\{A,B,C\}[/latex]. Ta je relacija ocito antisimetricna, tranzitivna i refleksivna, pa je parcijalni uredjaj. No, i [latex]A[/latex] i [latex]B[/latex] su maksimalni.
'ave fun!
Sinisa
| ZELENIZUBNAPLANETIDOSADE (napisa): |
| Citat: | Za familiju podgrafova nekog grafa G definiramo maksimalni podgraf Gmax za tu familiju ukoliko iz " Gmax ulozen u G' " slijedi Gmax=G'
Komponenta povezanosti C grafa G je maksimalni podgraf neke familije povezanih podgrafova od G. |
|
skvik!
Komponenta povezanoti C grafa G je maksimalni podgraf familije svih povezanih podgrafova od G.
Maksimalni element parc. uredjenog skupa nije nuzno jedinstven! Npr. imamo tri objekta,  , ,  i i  , te neka je relacija , te neka je relacija 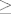 zadana sa zadana sa 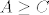 i i 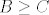 , te , te 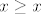 za sve za sve 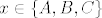 . Ta je relacija ocito antisimetricna, tranzitivna i refleksivna, pa je parcijalni uredjaj. No, i . Ta je relacija ocito antisimetricna, tranzitivna i refleksivna, pa je parcijalni uredjaj. No, i  i i  su maksimalni. su maksimalni.
'ave fun!
Sinisa
_________________
Oslobodjen Senata.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
|
| [Vrh] |
|
cinik
Forumaš(ica)


Pridružen/a: 27. 04. 2003. (23:34:09)
Postovi: (1FB)16
Spol: 
Lokacija: /proc/sys/cpu/
|
|
| [Vrh] |
|
koryanshea
Forumaš(ica)


Pridružen/a: 12. 10. 2003. (23:50:23)
Postovi: (442)16
Spol: 
Lokacija: Bebop (converted interplanetary trawler)
|
 Postano: 19:33 sri, 24. 8. 2005 Naslov: Postano: 19:33 sri, 24. 8. 2005 Naslov: |
    |
|
|
cMi :( treba mi pomoc da popunim rupe u dokazu teorema dualnosti za transportni problem!
Dakle, TM je formuliran ovako:
Neka je X dopustivi transport, [i]u[/i] i [i]v[/i] dopustive takse. Tada je ekvivalentno:
1) X je optimalni transport primarnog, a [i]u[/i] i [i]v[/i] su optimalne takse dualnog problema
2) z(X)=z(u,v)
3) vrijedi uvjet optimalnosti, tj. x[size=8]ij[/size]>0 => u[size=8]i[/size]+v[size=8]j[/size]=c[size=8]ij[/size].
I onda ide dokaz: prvo pokazemo da je 2)<=>3)
onda dokazemo da 2)=>1)
dokaz za 1)=>2) cak ni iz dva pokusaja nije dovrsen na predavanjima, a u skripti njegov misterij ostaje netaknut. tamo izgleda ovako:
[img]http://161.53.8.14/~iradocaj/cak_trans1.jpg[/img]
[img]http://161.53.8.14/~iradocaj/cak_trans2.jpg[/img]
zanemarit cemo tipfeler nejednakosti umjesto jednakosti u drugom redu. :)
dakle, pretpostavili smo suprotno. ne razumijem zasto to implicira da su vrhovi [i]i[/i] i [i]j[/i] incidentni svaki s jos bar dva luka, niti sta bi mogli povecati ako nisu (da, to je rupa u recenici :)).
a onda idu ove dvije moguce situacije, nije mi jasno zasto je to bitno niti sta one impliciraju, posto s njima dokaz zavrsava (pardon, nisam ukljucila onu kockicu na kraju dokaza kad sam cropala).
hvala na svakoj pomoci :)
cMi  treba mi pomoc da popunim rupe u dokazu teorema dualnosti za transportni problem! treba mi pomoc da popunim rupe u dokazu teorema dualnosti za transportni problem!
Dakle, TM je formuliran ovako:
Neka je X dopustivi transport, u i v dopustive takse. Tada je ekvivalentno:
1) X je optimalni transport primarnog, a u i v su optimalne takse dualnog problema
2) z(X)=z(u,v)
3) vrijedi uvjet optimalnosti, tj. xij>0 ⇒ ui+vj=cij.
I onda ide dokaz: prvo pokazemo da je 2)⇔3)
onda dokazemo da 2)⇒1)
dokaz za 1)⇒2) cak ni iz dva pokusaja nije dovrsen na predavanjima, a u skripti njegov misterij ostaje netaknut. tamo izgleda ovako:


zanemarit cemo tipfeler nejednakosti umjesto jednakosti u drugom redu. 
dakle, pretpostavili smo suprotno. ne razumijem zasto to implicira da su vrhovi i i j incidentni svaki s jos bar dva luka, niti sta bi mogli povecati ako nisu (da, to je rupa u recenici  ). ).
a onda idu ove dvije moguce situacije, nije mi jasno zasto je to bitno niti sta one impliciraju, posto s njima dokaz zavrsava (pardon, nisam ukljucila onu kockicu na kraju dokaza kad sam cropala).
hvala na svakoj pomoci 
_________________  "Download the files to a non-networked, firewalled computer."
- Dr. Elizabeth Weir |
|
| [Vrh] |
|
Gost
|
 Postano: 14:48 čet, 25. 8. 2005 Naslov: Postano: 14:48 čet, 25. 8. 2005 Naslov: |
    |
|
|
dakle ovako:
Tm tvrdi da su (u,v) optimalne takse i X optimalni transport akko vrijedi da je z'(u,v)=z(X).
Pa onda sad uzmeš da su (u,v) neke dopustive takse i X neki dopustivi transport za koje vrijedi da je z'(u,v)=z(X) i hoćeš pokazati da su (u,v) i X optimalni (tj. da je X dopustiv transport takav da je njegova cijena z(X)minimalna i (u,v) dopustive takse takve da je cijena z'(u,v) maksimalna.
Da stvarno jesu odabrani (u,v) i X optimalni proizlazi odmah iz slabe dualnosti jer ona kaže da za svaki dopustivi transport x' i svake dopustive takse (u',v') je z'(u',v')<=z(X') pa onda budući je
z'(u',v')<=z(X),a z(X)=z'(u,v) slijedi da je z'(u',v')<=z'(u,v) za svaki (u',v') pa su (u,v) optimalane.Analogno za X, z(X)=z'(u,v)<=z(X') za svaki X' dopustivi pa je X optimalan (tj. cijena z(X) mu je min).
[b]Obratno[/b] neka su (u,v) optimalne takse i neka je X optimalan transport; tvrdimo da je z'(u,v)=z(X).
Sada transportu pridružiš bipartitni graf u kojemu spojnica između i-tog i j-tog vrha predstavlja transport između i-tog proizvođača i j-tog trgovca.Ukoliko na toj dionici transporta nema onda ta spojnica nije ucrtana, a ako ima onda je xij(>0) količina robe koja se prevozi na toj ruti.I sada je za dokaz našeg obrata dovoljno dokazati da je podgraf toga grafa za koji vrijedi da je ui + vj=cij na svakoj njegovoj spojnici zapravo cijeli graf transporta jer onda je xij>0 => ui + vj=cij za svaki i,j pa je z'(u,v)=z(X) što i trebaš
To dokazuješ tako da pretpostaviš suprotno tj. da postoji u grafu neka spojnica koja nije u podgrafu tj. spojnica takva da je xij>0, a ui +vj<cij
S time da trebaš primjetiti da su i vrh i i vrh j nužno spojeni spojnicama sa neka dva vrha iz onog podgrafa maloprije opisanog (u skripti prof. to zove saturirani podgraf) recimo da su i-k i j-l te spojnice podgrafa (u skripti ima slika kako to izgleda).Jer ukoliko bar jedna od tih spojnica i-k ili j-l ne bi bila u podgrafu onda bi mogli povećati taksu ui (ako i-k nije u podgrafu) tako da je još uvijek ui + vj<=cij (jer je po pretpostavci ui+vj<cij) što onda znači da je cijena z(u,v) povećana a to je u suprotnosti sa pretp. da su (u,v) optimalne takse (tj. takve da je cijena z'
max).Analogno ako j-l nije u podgrafu.
Dakle još jednom možda iz drugog kuta ako su (u,v) optimalne takse (što jesu po pretp.ovog smjera dokaza) onda ne možeš povećavati niti jednu komponentu tih taksi jer svako povećanje pridonosi povećanju ukupne cijene z' što nije moguće zbog optimalnosti od (u,v).Znači ako su (u,v) optimalne takse onda ne možemo povećati ni ui ni vj a to onda povlači da su i i-k i j-l spojnice u onom podgrafu (jer za sve spojnice podgrafa vrijedi da u + v=c pa bi bilo kakvo povećanje narušilo dopustivost taksi (u,v)).
Znači (u,v) optimalne <=> i-k i j-l su iz podgrafa.
Sada imaš dva moguća slučaja koja oba želiš dotjerati do kontradikcije.
1.) Vrhovi i i j su u istoj komponenti povezanosti podgrafa.
To znači da se i i j mogu spojiti putem sa svaka dva vrha sat.podgrafa pa specijalno postoji spojnica između vrhova k i l (jer spojnica i-j po pretp. nije u sat. podgrafu a drugog načina da se spoje k i l [b]unutar podgrafa [/b] nema.) To je dost dobro u skripti nacrtano.I sada kad spojiš k i l imaš ciklus u kojem možeš smanjivati/povećavati transport (broj jedinica robe) a da opet svi proizvođači se riješe sve robe i da trgovci podmire sva potraživanja.Konkretno smanjiš za nekih s jedinica robe xij i xlk, a za istih s povećaš xik i xlj.U skripti je usput krivo označeno tj obrnuto ondje gdje povečavaš je označeno sa -s a ondje gdje smanjuješ sa s.To povećavanje/smanjivanje si možeš objasniti na način da kad smanjiš isporuku na ruti i-j onda proizođač i ima s jedinica robe viška pa ih šalje u k rutom i-k, a da ne bi trgovac k dobio višak robe proizvođač l mu smanjuje isporuku na ruti l-k i tu robi šalje ka j kod kojega je manjak jer smo na početku smanjili isporuku pa su opet svi isporučili i svi primili količine koje su trebali.Međutim cijena transporta se promjenila jer cijene transporta na pojedinim dionicama se naravno razlikuju i ta promjena je negativna (u skripti ima račun kratki) što znači da smo smanjili cijenu z(X)
što je u kontradikciji s pretp. da je X optimalan (tj da mu je cijena z(X) min) pa smo rješili prvi slučaj.
2.)Vrhovi i i j se nalaze u različitim komp. povezanosti
Sada u onoj komp. povezanosti u kojoj je vrh i (proizvođač) sve takse u
(dakle na strani proizvođača) povećamo za neki c a sve takse v (na strani trgovaca) smanjimo za c pa u cijelom sat. podgrafu stanje ostaje nepromjenjeno međutim na ruti i-j smo podigli cijenu za c (jer vrh j nije u onoj komp. povezanosti u kojoj smo izjednačili razlike) dakle povećali smo z' što je u suprotnosti sa pretp. da je z'(u,v) max. tj. da su takse (u,v) optimalne pa smo i drugi dio riješili.
I to bi bilo to uglavnom. Nadam se da je pomoglo.
dakle ovako:
Tm tvrdi da su (u,v) optimalne takse i X optimalni transport akko vrijedi da je z'(u,v)=z(X).
Pa onda sad uzmeš da su (u,v) neke dopustive takse i X neki dopustivi transport za koje vrijedi da je z'(u,v)=z(X) i hoćeš pokazati da su (u,v) i X optimalni (tj. da je X dopustiv transport takav da je njegova cijena z(X)minimalna i (u,v) dopustive takse takve da je cijena z'(u,v) maksimalna.
Da stvarno jesu odabrani (u,v) i X optimalni proizlazi odmah iz slabe dualnosti jer ona kaže da za svaki dopustivi transport x' i svake dopustive takse (u',v') je z'(u',v')⇐z(X') pa onda budući je
z'(u',v')⇐z(X),a z(X)=z'(u,v) slijedi da je z'(u',v')⇐z'(u,v) za svaki (u',v') pa su (u,v) optimalane.Analogno za X, z(X)=z'(u,v)⇐z(X') za svaki X' dopustivi pa je X optimalan (tj. cijena z(X) mu je min).
Obratno neka su (u,v) optimalne takse i neka je X optimalan transport; tvrdimo da je z'(u,v)=z(X).
Sada transportu pridružiš bipartitni graf u kojemu spojnica između i-tog i j-tog vrha predstavlja transport između i-tog proizvođača i j-tog trgovca.Ukoliko na toj dionici transporta nema onda ta spojnica nije ucrtana, a ako ima onda je xij(>0) količina robe koja se prevozi na toj ruti.I sada je za dokaz našeg obrata dovoljno dokazati da je podgraf toga grafa za koji vrijedi da je ui + vj=cij na svakoj njegovoj spojnici zapravo cijeli graf transporta jer onda je xij>0 ⇒ ui + vj=cij za svaki i,j pa je z'(u,v)=z(X) što i trebaš
To dokazuješ tako da pretpostaviš suprotno tj. da postoji u grafu neka spojnica koja nije u podgrafu tj. spojnica takva da je xij>0, a ui +vj<cij
S time da trebaš primjetiti da su i vrh i i vrh j nužno spojeni spojnicama sa neka dva vrha iz onog podgrafa maloprije opisanog (u skripti prof. to zove saturirani podgraf) recimo da su i-k i j-l te spojnice podgrafa (u skripti ima slika kako to izgleda).Jer ukoliko bar jedna od tih spojnica i-k ili j-l ne bi bila u podgrafu onda bi mogli povećati taksu ui (ako i-k nije u podgrafu) tako da je još uvijek ui + vj⇐cij (jer je po pretpostavci ui+vj<cij) što onda znači da je cijena z(u,v) povećana a to je u suprotnosti sa pretp. da su (u,v) optimalne takse (tj. takve da je cijena z'
max).Analogno ako j-l nije u podgrafu.
Dakle još jednom možda iz drugog kuta ako su (u,v) optimalne takse (što jesu po pretp.ovog smjera dokaza) onda ne možeš povećavati niti jednu komponentu tih taksi jer svako povećanje pridonosi povećanju ukupne cijene z' što nije moguće zbog optimalnosti od (u,v).Znači ako su (u,v) optimalne takse onda ne možemo povećati ni ui ni vj a to onda povlači da su i i-k i j-l spojnice u onom podgrafu (jer za sve spojnice podgrafa vrijedi da u + v=c pa bi bilo kakvo povećanje narušilo dopustivost taksi (u,v)).
Znači (u,v) optimalne ⇔ i-k i j-l su iz podgrafa.
Sada imaš dva moguća slučaja koja oba želiš dotjerati do kontradikcije.
1.) Vrhovi i i j su u istoj komponenti povezanosti podgrafa.
To znači da se i i j mogu spojiti putem sa svaka dva vrha sat.podgrafa pa specijalno postoji spojnica između vrhova k i l (jer spojnica i-j po pretp. nije u sat. podgrafu a drugog načina da se spoje k i l unutar podgrafa nema.) To je dost dobro u skripti nacrtano.I sada kad spojiš k i l imaš ciklus u kojem možeš smanjivati/povećavati transport (broj jedinica robe) a da opet svi proizvođači se riješe sve robe i da trgovci podmire sva potraživanja.Konkretno smanjiš za nekih s jedinica robe xij i xlk, a za istih s povećaš xik i xlj.U skripti je usput krivo označeno tj obrnuto ondje gdje povečavaš je označeno sa -s a ondje gdje smanjuješ sa s.To povećavanje/smanjivanje si možeš objasniti na način da kad smanjiš isporuku na ruti i-j onda proizođač i ima s jedinica robe viška pa ih šalje u k rutom i-k, a da ne bi trgovac k dobio višak robe proizvođač l mu smanjuje isporuku na ruti l-k i tu robi šalje ka j kod kojega je manjak jer smo na početku smanjili isporuku pa su opet svi isporučili i svi primili količine koje su trebali.Međutim cijena transporta se promjenila jer cijene transporta na pojedinim dionicama se naravno razlikuju i ta promjena je negativna (u skripti ima račun kratki) što znači da smo smanjili cijenu z(X)
što je u kontradikciji s pretp. da je X optimalan (tj da mu je cijena z(X) min) pa smo rješili prvi slučaj.
2.)Vrhovi i i j se nalaze u različitim komp. povezanosti
Sada u onoj komp. povezanosti u kojoj je vrh i (proizvođač) sve takse u
(dakle na strani proizvođača) povećamo za neki c a sve takse v (na strani trgovaca) smanjimo za c pa u cijelom sat. podgrafu stanje ostaje nepromjenjeno međutim na ruti i-j smo podigli cijenu za c (jer vrh j nije u onoj komp. povezanosti u kojoj smo izjednačili razlike) dakle povećali smo z' što je u suprotnosti sa pretp. da je z'(u,v) max. tj. da su takse (u,v) optimalne pa smo i drugi dio riješili.
I to bi bilo to uglavnom. Nadam se da je pomoglo.
|
|
| [Vrh] |
|
koryanshea
Forumaš(ica)


Pridružen/a: 12. 10. 2003. (23:50:23)
Postovi: (442)16
Spol: 
Lokacija: Bebop (converted interplanetary trawler)
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
vili
Forumaš(ica)


Pridružen/a: 08. 06. 2005. (22:40:59)
Postovi: (14A)16
Spol: 
Lokacija: Keglić
|
 Postano: 13:44 sri, 27. 9. 2006 Naslov: Postano: 13:44 sri, 27. 9. 2006 Naslov: |
    |
|
|
[quote="Melkor"][quote="Anonymous"]1.) Vrhovi i i j su u istoj komponenti povezanosti podgrafa.
To znači da se i i j mogu spojiti putem sa svaka dva vrha sat.podgrafa pa specijalno postoji spojnica između vrhova k i l (jer spojnica i-j po pretp. nije u sat. podgrafu a drugog načina da se spoje k i l [b]unutar podgrafa [/b] nema.)[/quote]
Nije li tu zaključak da se k i l mogu spojiti nekim putom u saturiranom podgrafu? Nije mi jasno zašto su spojeni baš spojnicom, tj. zašto je na luku (l,k) x_lk>0.
Zbilja mučan dokaz. Na predavanju je profesor krivo dokazao, u skripti dokaz nije dovršen, a ovaj dokaz nikako ne mogu shvatiti. :cry:[/quote]
Da, uistinu slijedi takav zaključak, a ne onaj kojeg je gost napisao. I mene je mučila ista stvar, a onda sam skužio da promet isto tako možeš prusmjeriti preko proizvoljnog puta da dobiješ jeftiniji transport. Probaj proučit pa ak ti i dalje nije jasno javi mi se na PM.
| Melkor (napisa): | | Anonymous (napisa): | 1.) Vrhovi i i j su u istoj komponenti povezanosti podgrafa.
To znači da se i i j mogu spojiti putem sa svaka dva vrha sat.podgrafa pa specijalno postoji spojnica između vrhova k i l (jer spojnica i-j po pretp. nije u sat. podgrafu a drugog načina da se spoje k i l unutar podgrafa nema.) |
Nije li tu zaključak da se k i l mogu spojiti nekim putom u saturiranom podgrafu? Nije mi jasno zašto su spojeni baš spojnicom, tj. zašto je na luku (l,k) x_lk>0.
Zbilja mučan dokaz. Na predavanju je profesor krivo dokazao, u skripti dokaz nije dovršen, a ovaj dokaz nikako ne mogu shvatiti.  |
Da, uistinu slijedi takav zaključak, a ne onaj kojeg je gost napisao. I mene je mučila ista stvar, a onda sam skužio da promet isto tako možeš prusmjeriti preko proizvoljnog puta da dobiješ jeftiniji transport. Probaj proučit pa ak ti i dalje nije jasno javi mi se na PM.
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
|














