Radi se o Lemi 7.10. Neka je C simetricna matrica i [latex]q(y)=y^\tau Cy[/latex]. Tada je [latex]\lambda[/latex] svojstvena vrijednost od C AKKO je [latex]\lambda[/latex] kriticna tocka restrikcije [latex]\displaystyle q \vert_{S^{n-1}}[/latex]
Dokaz:
Neka je [latex]\lambda[/latex], y, [latex]\|y\|=1[/latex], svojstven par od C i neka je [latex]\gamma[/latex] glatka regularna krivulja definirana na nekoj okolini nule sa vrijednostima u [latex]S^{n-1}=\{x \in R^n : \|x\|=1\}[/latex] i takva da [latex]\gamma(0)=y[/latex]. Tada je [latex]y^\tau \gamma'(0)=0[/latex] jer je [latex]\|\gamma(t)\|=1[/latex] konstantna funkcija i:
[latex]\displaystyle 0=\frac d{dt}\|\gamma(t)\|=\frac{\gamma(t)}{\|\gamma(t)\|}\cdot\gamma'(t)[/latex]
sto je u suprotnosti sa pretpostavkom o regularnosti krivulje gama :(
Ideje?
(ostatak dokaza koristi cinjenicu da je y ortogonalan na derivaciju game u nuli)
Radi se o Lemi 7.10. Neka je C simetricna matrica i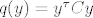 
. Tada je 
svojstvena vrijednost od C AKKO je kriticna tocka restrikcije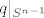 
Dokaz:
Neka je , y,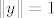 
, svojstven par od C i neka je 
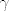glatka regularna krivulja definirana na nekoj okolini nule sa vrijednostima u 
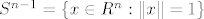i takva da 
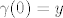. Tada je 
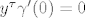jer je 
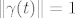konstantna funkcija i:
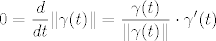
sto je u suprotnosti sa pretpostavkom o regularnosti krivulje gama 
Ideje?
(ostatak dokaza koristi cinjenicu da je y ortogonalan na derivaciju game u nuli)
_________________
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk
