|
[quote="EnigmaQ"](...)nije jasno zasto bi trebao postojati otvoren skup X podskup otvorenog skupa O za kojeg vrijedi gornje svojstvo iz zadatka?[/quote]
Prazan skup ima to svojstvo. Naprosto, formula
[latex]x,y\in\emptyset\Rightarrow x+y\in\emptyset[/latex]
je (trivijalno) istinita jer prazan skup uopće nema elemenata.
(Ispričavam se, nisam primijetio da je kolega Boris u međuvremenu odgovorio. :wink: )
----------
Po meni je veći problem sljedeći:
Ovako postavljen zadatak nije tipična primjena Zornove leme.
Naime, Zornova lema daje egzistenciju [u]maksimalnog[/u], a ne [u]najvećeg[/u] elementa u p.u.s.-u (uz odgovarajuće pretpostavke, naravno).
Zadatak koji je direktna primjena Zornove leme bi glasio ovako (traži se [u]maksimalni[/u] element U, tj. element U od kojeg nema većeg elementa V):
[quote="Popravljeni zadatak"]Neka je O podskup skupa realnih brojeva otvoren skup. Dokazite da postoji otvoren skup U podskup skupa O takav da je x,y \in{U} tada x+y \in{U} i ako je V podskup skupa O neki otvoreni skup takav da x,y \in{V} tada x+y \in{V} [b]onda U nije strogi podskup skupa V[/b].[/quote]
Zadatak koji si ti napisao (traži da se dokaže čak postojanje [u]najvećeg[/u] elementa U, tj. elementa U koji je veći od svakog drugog elementa V):
[quote="EnigmaQ"]Neka je O podskup skupa realnih brojeva otvoren skup. Dokazite da postoji otvoren skup U podskup skupa O takav da je x,y \in{U} tada x+y \in{U} i ako je V podskup skupa O neki otvoreni skup takav da x,y \in{V} tada x+y \in{V} onda je V podskup skupa U.[/quote]
Štoviše, tvrdnja koju si ovako formulirao ne mora vrijediti. Evo protuprimjera:
O=<-oo,-1>u<1,+oo>
Dva skupa koja imaju spomenuto svojstvo su
U=<-oo,-1> i U=<1,+oo>.
Obojica su maksimalni s tim svojstvom. Npr. kad bismo skupu <-oo,-1> dodali još neki element a>1, onda bi on morao i sadržavati sve brojeve <-oo,-1+a> pa bi specijalno sadržavao i 0, a to nije moguće jer 0 nije iz O. Analogno je <1,+oo> maksimalan.
Ipak, nijedan od skupova <-oo,-1> i <1,+oo> nije najveći jer ne sadrže jedan drugog.
-----------
Dakle, moguće su razne stvari:
-može postojati više maksimalnih podskupova i u tom slučaju nema najvećeg, to je npr. za O=<-oo,-1>u<1,+oo>
-može postojati najveći podskup, to je npr. za O=<1,+oo>
-nekad je čak prazan skup maksimalan i u tom slučaju je on i najveći, to je npr. za O=<-1,1>
Važno je razlikovati pojmove "maksimalni element" i "najveći element". :!: :!: :!:
| EnigmaQ (napisa): | | (...)nije jasno zasto bi trebao postojati otvoren skup X podskup otvorenog skupa O za kojeg vrijedi gornje svojstvo iz zadatka? |
Prazan skup ima to svojstvo. Naprosto, formula
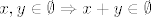
je (trivijalno) istinita jer prazan skup uopće nema elemenata.
(Ispričavam se, nisam primijetio da je kolega Boris u međuvremenu odgovorio.  ) )
----------
Po meni je veći problem sljedeći:
Ovako postavljen zadatak nije tipična primjena Zornove leme.
Naime, Zornova lema daje egzistenciju maksimalnog, a ne najvećeg elementa u p.u.s.-u (uz odgovarajuće pretpostavke, naravno).
Zadatak koji je direktna primjena Zornove leme bi glasio ovako (traži se maksimalni element U, tj. element U od kojeg nema većeg elementa V):
| Popravljeni zadatak (napisa): | | Neka je O podskup skupa realnih brojeva otvoren skup. Dokazite da postoji otvoren skup U podskup skupa O takav da je x,y \in{U} tada x+y \in{U} i ako je V podskup skupa O neki otvoreni skup takav da x,y \in{V} tada x+y \in{V} onda U nije strogi podskup skupa V. |
Zadatak koji si ti napisao (traži da se dokaže čak postojanje najvećeg elementa U, tj. elementa U koji je veći od svakog drugog elementa V):
| EnigmaQ (napisa): | | Neka je O podskup skupa realnih brojeva otvoren skup. Dokazite da postoji otvoren skup U podskup skupa O takav da je x,y \in{U} tada x+y \in{U} i ako je V podskup skupa O neki otvoreni skup takav da x,y \in{V} tada x+y \in{V} onda je V podskup skupa U. |
Štoviše, tvrdnja koju si ovako formulirao ne mora vrijediti. Evo protuprimjera:
O=←oo,-1>u<1,+oo>
Dva skupa koja imaju spomenuto svojstvo su
U=←oo,-1> i U=<1,+oo>.
Obojica su maksimalni s tim svojstvom. Npr. kad bismo skupu ←oo,-1> dodali još neki element a>1, onda bi on morao i sadržavati sve brojeve ←oo,-1+a> pa bi specijalno sadržavao i 0, a to nije moguće jer 0 nije iz O. Analogno je <1,+oo> maksimalan.
Ipak, nijedan od skupova ←oo,-1> i <1,+oo> nije najveći jer ne sadrže jedan drugog.
-----------
Dakle, moguće su razne stvari:
-može postojati više maksimalnih podskupova i u tom slučaju nema najvećeg, to je npr. za O=←oo,-1>u<1,+oo>
-može postojati najveći podskup, to je npr. za O=<1,+oo>
-nekad je čak prazan skup maksimalan i u tom slučaju je on i najveći, to je npr. za O=←1,1>
Važno je razlikovati pojmove "maksimalni element" i "najveći element".   
|







