[latex] $Dokazi da za strogo pozitivnu (diskretnu) slucajnu varijablu $X$ vrijedi nejednakost $E(X^{-1})\geq(EX)^{-1}$. Kada pritom vrijedi nejednakost?$ [/latex]
dokaz nejednakosti sam proveo ovako:
[latex]\displaystyle E(X^{-1})=\sum_k \frac 1k p_k\geq \sum_k \frac 1k \geq \frac1{\sum_k k}\geq \frac 1{\sum_k k\cdot p_k}=(EX)^{-1}[/latex]
Tvrdnja "razlomak pod sumom je manji ili jednak od sume razlomaka" mi je djelovao dovoljno razumno ali ga nisam posebno raspisivao. Nekakva pretpostavka slijedeci tu liniju rezoniranja bi bila da jednakost vrijedi samo kada je X konstanta.
Ima li smisla ovo sto pricam i da li bi jos stogod trebalo dodati da bi se zadatak smatrao "zadovoljavajuce rijesen"?

dokaz nejednakosti sam proveo ovako:
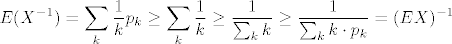
Tvrdnja "razlomak pod sumom je manji ili jednak od sume razlomaka" mi je djelovao dovoljno razumno ali ga nisam posebno raspisivao. Nekakva pretpostavka slijedeci tu liniju rezoniranja bi bila da jednakost vrijedi samo kada je X konstanta.
Ima li smisla ovo sto pricam i da li bi jos stogod trebalo dodati da bi se zadatak smatrao "zadovoljavajuce rijesen"?
_________________

Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk





