| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 14:25 sri, 21. 9. 2005 Naslov: Zadatak sa roka 21.09.2005 |
    |
|
|
[b]Zadan je linearni operator T : P_2 -> P_2 sa
T(a+bt+ct^2)=a+b+c+(a+3b)t+(a-b+2c)t^2
Odredite mu matrični prikaz u bazi B={1-t, t-t^2,1+t^2}. Nadalje, odredite mu po jednu bazu za jezgru i sliku.
Je li T monomorfizam, epimorfizam, izomorfizam?[/b]
Uglavnom, dođem do zaključka da je dimenzija slike jednaka dimenziji kodomene i(slijedi iz teorema o rangu i defektu) da je jezgra trivijalna.
Napisao sam(samo) - da je T monomorfizam.
Hoće li mi zbog toga oduzeti bodove?
Nisam napisao da je T izomorfizam, jesam li uopće trebao?
Nije li dovoljno reći da je T monomorfizam pa da sam rekao da je T izomorfizam, s obzirom da operator putuje između konačnodimenzionalnih v. prostora?
Štogore, riješio sam na ispitu samo dva zadatka tako da ako mi se oduzme taj bod(pola boda) - ne prolazim! :roll:
Zadan je linearni operator T : P_2 -> P_2 sa
T(a+bt+ct^2)=a+b+c+(a+3b)t+(a-b+2c)t^2
Odredite mu matrični prikaz u bazi B={1-t, t-t^2,1+t^2}. Nadalje, odredite mu po jednu bazu za jezgru i sliku.
Je li T monomorfizam, epimorfizam, izomorfizam?
Uglavnom, dođem do zaključka da je dimenzija slike jednaka dimenziji kodomene i(slijedi iz teorema o rangu i defektu) da je jezgra trivijalna.
Napisao sam(samo) - da je T monomorfizam.
Hoće li mi zbog toga oduzeti bodove?
Nisam napisao da je T izomorfizam, jesam li uopće trebao?
Nije li dovoljno reći da je T monomorfizam pa da sam rekao da je T izomorfizam, s obzirom da operator putuje između konačnodimenzionalnih v. prostora?
Štogore, riješio sam na ispitu samo dva zadatka tako da ako mi se oduzme taj bod(pola boda) - ne prolazim! 
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
| Postano: 15:13 sri, 21. 9. 2005 Naslov: Re: Zadatak sa roka 21.09.2005 |
|
|
|
Pretpostavit cu da si dobro dobio da je Ker trivijalna. 8)
[quote="Vincent Van Ear"]Nije li dovoljno reći da je T monomorfizam pa da sam rekao da je T izomorfizam, s obzirom da operator putuje između konačnodimenzionalnih v. prostora?[/quote]
Primjer: [latex]f: \mathbb{R} \rightarrow \mathbb{R}^2,\ f(x) = (x,0)[/latex]
Mislim da ces se sloziti da je to injektivni homomorfizam, dakle monomorfizam, a ipak nije bijektivan (dakle, izomorfizam), iako "putuje između konačnodimenzionalnih v. prostora". :)
Dakle, [b]ako[/b] je izomorfizam, to si trebao i napisati. :| Ne znam kako ide bodovanje... :?
Pretpostavit cu da si dobro dobio da je Ker trivijalna. 
| Vincent Van Ear (napisa): | | Nije li dovoljno reći da je T monomorfizam pa da sam rekao da je T izomorfizam, s obzirom da operator putuje između konačnodimenzionalnih v. prostora? |
Primjer: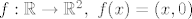 
Mislim da ces se sloziti da je to injektivni homomorfizam, dakle monomorfizam, a ipak nije bijektivan (dakle, izomorfizam), iako "putuje između konačnodimenzionalnih v. prostora". 
Dakle, ako je izomorfizam, to si trebao i napisati.  Ne znam kako ide bodovanje... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
| Postano: 15:26 sri, 21. 9. 2005 Naslov: Re: Zadatak sa roka 21.09.2005 |
|
|
|
[quote="vsego"]Pretpostavit cu da si dobro dobio da je Ker trivijalna. 8)
[quote="Vincent Van Ear"]Nije li dovoljno reći da je T monomorfizam pa da sam rekao da je T izomorfizam, s obzirom da operator putuje između konačnodimenzionalnih v. prostora?[/quote]
Primjer: [latex]f: \mathbb{R} \rightarrow \mathbb{R}^2,\ f(x) = (x,0)[/latex]
Mislim da ces se sloziti da je to injektivni homomorfizam, dakle monomorfizam, a ipak nije bijektivan (dakle, izomorfizam), iako "putuje između konačnodimenzionalnih v. prostora". :)
Dakle, [b]ako[/b] je izomorfizam, to si trebao i napisati. :| Ne znam kako ide bodovanje... :?[/quote]
Uvažujem tvoj trud(stvarno :) ) i ispravljam sebe:
Vsego, mi smo imali dakle ovaj teorem:
Neka su V i W konačnodim. v. prostori [b]jednakih[/b](to mi je falilo) dimenzija i A sa V u W linearan.
Tada su sljedeće tvrdnje [b]ekvivalentne[/b]:
a) A je injekcija(monomorfizam)
b)A je surjekcija(epimorfizam)
c)A je bijekcija(izomorfizam)
Misliš li sada da sam trebao spomenuti da je T bijekcija :?: :(
| vsego (napisa): | Pretpostavit cu da si dobro dobio da je Ker trivijalna.
| Vincent Van Ear (napisa): | | Nije li dovoljno reći da je T monomorfizam pa da sam rekao da je T izomorfizam, s obzirom da operator putuje između konačnodimenzionalnih v. prostora? |
Primjer: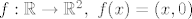
Mislim da ces se sloziti da je to injektivni homomorfizam, dakle monomorfizam, a ipak nije bijektivan (dakle, izomorfizam), iako "putuje između konačnodimenzionalnih v. prostora".
Dakle, ako je izomorfizam, to si trebao i napisati. Ne znam kako ide bodovanje... |
Uvažujem tvoj trud(stvarno ) i ispravljam sebe:
Vsego, mi smo imali dakle ovaj teorem:
Neka su V i W konačnodim. v. prostori jednakih(to mi je falilo) dimenzija i A sa V u W linearan.
Tada su sljedeće tvrdnje ekvivalentne:
a) A je injekcija(monomorfizam)
b)A je surjekcija(epimorfizam)
c)A je bijekcija(izomorfizam)
Misliš li sada da sam trebao spomenuti da je T bijekcija  
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol:
Lokacija: /sbin/init
|
| Postano: 15:31 sri, 21. 9. 2005 Naslov: |
|
|
|
Ispit provjerava [b]znanje[/b] - ako ti nisi napisao da je bijekcija, kako asistent moze znati da znas ovo sto si napisao tu na Forumu? :-k
Meni je taj argument poznat (i jasan ;)), no asistent jednostavno ne moze znati da je i tebi to poznato ako ne napises. :( Zato sam i stavio (ocito) los primjer, koristeci ono sto si rekao da si napisao na ispitu. :)
Svejedno, ne zelim prejudicirati sto ce asistent napraviti. :| Ako se desi ono tragicno, odi na zalbe i pokusaj objasniti... :)
Ispit provjerava znanje - ako ti nisi napisao da je bijekcija, kako asistent moze znati da znas ovo sto si napisao tu na Forumu? 
Meni je taj argument poznat (i jasan  ), no asistent jednostavno ne moze znati da je i tebi to poznato ako ne napises. Zato sam i stavio (ocito) los primjer, koristeci ono sto si rekao da si napisao na ispitu.
Svejedno, ne zelim prejudicirati sto ce asistent napraviti. Ako se desi ono tragicno, odi na zalbe i pokusaj objasniti...
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
|
).